Урок. " Квадратні рівняння"

Тема. Розв’язування квадратних рівнянь з параметрами. Ділова гра

Мета: домогтися засвоєння учнями алгоритмів розв’язування квадратних рівнянь з параметрами від найпростіших до більш складних; перевірити рівень засвоєння змісту основних понять теми «Квадратні рівняння» та рівень умінь, сформованих під час вивчення теми.

Хід уроку

1. Квадратні рівняння найпростіших видів вавилонські математики вміли розв’язувати ще 4 тисячі років тому. Ми вже вміємо розв’язувати деякі квадратні рівняння. Сьогодні ми відшліфуємо ще одну грань цього діаманту. Ця грань « Квадратні рівняння з параметрами». Для цього пригадаємо

• Які рівняння ми називаємо квадратними?
• Що таке неповні квадратні рівняння?
• Назвіть формулу коренів квадратного рівняння?
• Який вираз ми називаємо дискримінантом?
• Як дискримінант «розрізняє» кількість коренів квадратного рівняння?
• Яке квадратного рівняння ми називаємо зведеним?
• Що таке рівняння з параметром? (рівняння у якого деякі числові коефіцієнти замінені буквеними  виразами, які можуть приймати будь які значення)

      II.  Клас поділений на команди, які є виробничою фірмою. Проведення та результати тендеру вказують на черговість купівлі «ресурсів» концернами. Кожна команда бере позику 6 грошових одиниць. Цими грошовими одиницями вони будуть розраховуватися за ресурси (умови задач). Створивши продукцію (розв’язавши рівняння) кожна команда виходить на аукціон де буде «продавати» свої вироби.

• Правильно розв’язане рівняння -100% прибутку від номінальної вартості;
• Невеликі неточності- 50% прибутку від номінальної вартості;
• Частково розв’язані- за вартістю сировини;
• Не розв’язані- брак 0 грошових одиниць.

Всі умови завдань подаються концернам на аркушах або виводяться через проектор на дошку.

Тендер. Групова робота. ( відповіді на питання записати на окремому аркуші і голова концерну піднімає їх над столом. Всі одразу)

Умови тендеру:

1.Чому дорівнює сума коренів рівняння  x²+5x-10=0:

      A) 5;                                Б)-5;                           В)-10;                         Г) 10?

2.Чому дорівнює добуток коренів рівняння 2x²-14x+12=0:

      А) 12;                              Б)14;                          В)6;                             Г)7?

3.Яке з даних рівнянь не є квадратним?

      А) x²=0;                   Б) x²+x=0;                  В)x³+x=0;              Г)x²+x-2=0.

4.Яке з поданих рівнянь є зведеним квадратним рівнянням?

      А)16-6x+x²=0;        Б)-х²+8х-7=0;          В)2х²+6х+8=0;       Г)х-0,5х²+3=0.

5.Чому дорівнює старший коефіцієнт, другий коефіцієнт і вільний член рівняння 7+3х²-2х=0?

      А)  а=7, в=3, с=-2            Б)  а=3, в=2, с=7;

      В)  а=-2, в=3, с =7;          Г)  а=3, в=-2, с=7.

Відповідь:  Б; В; В; А; Г, (визначаємо черговість закупівлі ресурсів. Швидкість і точність)

III. Банкіри видають позику  6 грошових одиниць кожній команді. Кожна команда купує собі рівняння згідно вартості лота та своєї черги.

1. Вартість 1 грошова одиниця.

 Розв’яжіть рівняння з параметром a:

1. ax²+6=0;
2. x²-4ax=0;
3. ax²-a²=0.

Відповідь: 1. а≥0 то x ϵ Ø;  а<0 то х=±

                     2.а=0 то х=0; а≠0 то х₁=0 і х₂=4а.

                     3.а<0 то x ϵ Ø;  а=0 то х- будь яке число; а>0 то х=±

 

2. Вартість 2 грошові одиниці.

При яких значеннях a рівняння має один корінь:

 1.3x²-(a²-2a)x=0;

 2.x²+(a+1)x+2,25=0;

 3.(a+5)x²-(a+6)x+3=0?

Відповідь: 1. 0 або 2;

                     2. -4 або 2;

                     3. -5; ±.

3) Вартість 3 грошові одиниці.

Для кожного значення параметра a розв’яжіть  рівняння:

        1.x²+(3a+1)x+2a²+a=0;

        2.a²x²-24ax-25=0;

          3.ax²-(a+1)x+1=0.

Відповідь:1.  а=-1 то х=1;   а≠-1 то х₁=а і х₂= -2а-1.

                    2. а=0 то  x ϵ Ø;  а≠0 то х₁=- і х₂=.

                    3.а=0 то х=1; а=1 то х=1; то х₁=1 і х₂=.

4) Вартість 4 грошові одиниці.

Для кожного значення параметра a розв’яжіть рівняння:

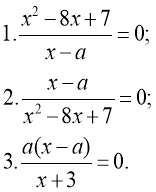
Відповідь: 1. а=1 то х=7; а=7 то х=1; то х₁=7 і х₂=1.

                     2. а=7 то   x ϵ Ø;  а= 1 то  x ϵ Ø;  ; то х=а.

                    3. а=-3 то   x ϵ Ø; а=0 то х будь яке число крім -3; то х=а.

5) Вартість 4 грошові одиниці.

 При яких значення параметра а рівняння

(a-2)x²+(2a-1)x+a²-4=0 є:

1)лінійним;

2)зведеним квадратним;

3)неповним незведеним квадратним рівнянням;

4)неповним зведеним квадратним рівнянням?

Після розв'язування рівняння в групах один представник показує його розв'язок біля дошки. Підраховуємо бали. Визначаємо успішні концерни і концерни банкроти (якщо є ).

IV. Сьогодні на уроці ми розглянули лише дуже маленьку часточку рівнянь що містять параметри. В подальшій своїй роботі ми ще будемо не один раз до них повертатися, щоб на закінчення курсу вивчення математики вільно орієнтуватися в даній темі і успішно пройти всі іспити де і які б вони не були.

І на кінець хочу звернути вашу увагу на постать видатного французького математика Франсуа Вієт. Його називають « батьком алгебри». За фахом він юрист. Був радником короля Генріха IV. Розшифровуючи за допомогою знань по математиці листи іспанського короля прискорив перемогу Франції у війні. Задля занять наукою нехтував їжею і сном. Усі його роботи по математиці мали стати підготовкою до створення великого астрономічного трактату, який, нажаль, не був закінчений. Тому я і вас закликаю ким би ви не мріяли стати – любіть математику. Вона скрізь потрібна.

V. Домашнє завдання. Повторити параграф 3, пункт 17- 19. Номера 692; 694. Підготуватися до письмової роботи.