Алгебра 8 клас Розвязування квадратних рівнянь

 Алгебра 8 клас

 Тема уроку. Розв’язування квадратних рівнянь

 Мета уроку: удосконалювати навички розв’язування квадратних рівнянь, нескладних текстових задач на складання квадратних рівнянь. Розвивати логічне мислення учнів, їх інтелектуальні здібності; виховувати інтерес до математики, віру в свої сили, уміння працювати колективно і самостійно.

Очікувані результати: учні повинні вміти розв’язувати квадратні рівняння.

Основні поняття: квадратні рівняння, неповні квадратні рівняння, формули дискримінанта та коренів квадратного рівняння.

Компетентності, що формуються: математична – уміння оперувати числовою інформацією, уміння розв’язувати нескладні квадратні рівняння; ключові – інформаційно-цифрова; соціальна і громадянська; спілкування державною мовою; вміння вчитися впродовж життя.

Обладнання: підручник, опорний конспект «Квадратні рівняння», проектор.                                                           

Тип уроку. Застосування знань та вмінь

 

                                                                Рівняння є найбільш серйозною і                                                                                          

                                                                 важливою річчю у математиці

                                                                  О. Лодж, англ. Математик

І. Організаційний етап

ІІ. Перевірка домашнього завдання

      Теоретична розминка

Слайд1. Закінчити речення

• Рівняння – це рівність,… ( яка містить невідомі числа, позначені буквами).
• Число, яке задовольняє рівняння, називають …(його коренем або розв’язком).
• Розв’язати рівняння – це означає …(знайти всі його корені або показати, що їх не існує).

Дати різні означення квадратного рівняння.

             Це – рівняння другого степеня з однією змінною.

              Це – рівняння виду , де х – змінна а,в,с – дані числа, причому

              Це – рівняння, ліва частина якого є многочлен другого степеня з однією змінною, а права – нуль.

• Які квадратні рівняння називаються неповними? Види неповних квадратних рівнянь…1)

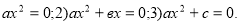
Слайд 2  Логічна задача 1    

 Усне коментоване розв’язання

                         

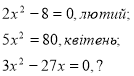
• Які ви знаєте способи розв’язування повних квадратних рівнянь?

              Це – спосіб виділення квадрата двочлена.

              Це – спосіб групування.

               За формулами:    де

Слайд 3. Логічна задача 2                                          

                                                                                  

На дошці двоє учнів розв’язують дані рівняння:

             перше – виділенням квадрата двочлена;

             друге – за формулами.

Підсумок першого етапу уроку. Рефлексія

Який висновок ви можете зробити для себе?

• Я вмію розв’язувати квадратні рівняння
• Я вдосконалю навички розв'язування квадратних рівнянь
• Я хочу і зможу досягти кращих результатів своєї роботи
• Мені цікаво розв’язувати квадратні рівняння

ІІІ. Формулювання мети і завдань уроку. Мотивація навчальної діяльності

Слово вчителя

Німецький фізик А. Ейнштейн писав: «Доводиться поділяти свій час між політикою і рівняннями. Однак рівняння набагато важливіші, оскільки політика існує тільки для даного моменту, а рівняння існуватимуть вічно».

Тому зараз ми з вами зробимо цікавий екскурс в історію виникнення квадратних рівнянь.

        Необхідність розв’язувати рівняння не тільки першого, а й другого степеня ще в давнину була викликана потребою розв’язувати задачі, пов’язані із знаходженням площі земельних ділянок та із земельними роботами військового характеру, а також із розвитком астрономії і самої математики.

      Квадратні рівняння вміли розв’язувати вавілоняни близько 2 тис. років до н.е. Застосовуючи сучасні алгебраїчні записи, можна сказати, що в їх клинописних текстах зустрічаються, крім неповних, і такі, наприклад, повні квадратні рівняння: 

Правила розв’язку цих рівнянь, викладене у вавілонських текстах, співпадає по суті із сучасним, але невідомо, яким чином дійшли вавілоняни до цього правила. Майже всі знайдені до цього часу клинописні тексти задач із розв’язками, викладені у вигляді рецептів, які не містять вказівок відносно того, яким способом вони знайдені.

      Не дивлячись на високий рівень розвитку алгебри в Вавилоні, в клинописних текстах відсутнє поняття від’ємного числа і загальні методи розв’язування квадратних рівнянь.

ІV. Застосування вмінь

 Двоє учнів на дошці розв’язують запропоновані рівняння.

Вчитель

Деякі види квадратних рівнянь, розв’язок яких зводиться до геометричних побудов, вміли розв’язувати старогрецькі математики. Приклади розв’язання рівнянь без звертання до геометрії дає Діофант Александрійський (ІІІ ст.). В шести із 13 його книг «Арифметика», що дійшли до нас, містяться задачі із розв’язками, в яких Діофант пояснює, як треба вибрати невідоме, щоб дістати розв’язок рівняння виду      

           Спосіб розв’язування повних квадратних рівнянь Діофант виклав у книжках  «Арифметика», які не збереглися.

Ось наприклад, одна із його задач:

Слайд 4.   

 Знайти два числа, знаючи, що їх сума дорівнює 20, а добуток 96.

Колективне розв’язання задачі.

          Задачі на квадратні рівняння зустрічаються в астрономічному трактаті «Ариабхаттиам», складеному в 449р. індійським математиком і астрономом Аріабхаттой. Другий індійський вчений Брахмагупта виклав загальне правило розв’язування квадратних рівнянь, зведених до єдиної канонічної форми:  додатне, коефіцієнти в і  с можуть бути від’ємними. Правило Брахмагупти по суті співпадає з нашим.

      В Стародавній Індії були поширені публічні змагання по розв’язуванню важких задач. В одній із стародавніх індійських книг з приводу цих змагань сказано так: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Задачі часто подавались у віршованій формі.

                    Ось одна із стародавніх задач знаменитого  індійського математика Бхаскари, 1114р.

         Підручник Г.П. Бевза, №1115:

Розділившись на дві зграї,

Збавлялись мавпи в гаї.

Одна восьма їх в квадраті

Танцювали, вельми раді,

А дванадцять на деревах

Підняли веселий регіт,

що навколо аж гуло.

Скільки їх всього було?

Колективна робота: аналіз задачі та складання рівняння.

Слайд 5. Рівняння 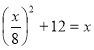 Бхаскара пише у вигляді:

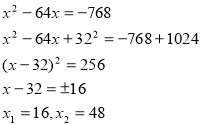
Відповідь: було 16 або 48 мавп.

Вчитель

В алгебраїчному трактаті аль – Хорезм дається класифікація лінійних і квадратних рівнянь. Автор нараховує 6 видів рівнянь, виражаючи їх наступним чином:

Слайд 6

1) «квадрати дорівнюють кореням», тобто

2) «квадрати дорівнюють числу»

3) «корені дорівнюють числу»

4) «квадрати і числа дорівнюють кореням»

5) «квадрати і корені дорівнюють числу»

6) «корені і числа дорівнюють квадратам»

Буквами a, в і c позначено лише додатні числа і аль – Хорезмі знаходить лише додатні корені.

Слайд 7. Задача. Квадрат і число 21 дорівнюють 10 кореням. Знайти корінь.

Розв’язання задачі на дошці з коментуванням.

Вчитель

Загальне правило розв’язування квадратних рівнянь, зведених до виду, сформулював німецький математик М. Штіфель (1487 – 1567). Виведенням формули розв’язування квадратних рівнянь загального вигляду займався Вієт. Проте своє твердження він висловлював лише для додатних коренів (від’ємних чисел він не визнавав).

       Італьянські математики Тарталья, Кардано, Бамбеллі серед перших врахували, крім додатних, і від’ємні корені.

       Лише завдяки працям нідерландського математика А. Жірара (1595 – 1632), а також Декарта, Ньютона та інших вчених спосіб розв’язування квадратних рівнянь набув сучасного вигляду.

 

V.   Підсумок уроку. Рефлексія

•                               розкажіть про свій емоційний стан під час уроку і в його кінці;
•                               що нового ви дізналися, чого навчились?
•                               як ви оцінюєте свою участь на уроці?

VІ. Домашнє завдання:

1. Вивчити всі формули коренів квадратного рівняння.
2. Розв’язати вправи на застосування формул.
3. Задача №1116.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

         Алгебра і початки аналізу,10 клас

Тема уроку. Розв’язування тригонометричних рівнянь.

Мета уроку. Набуття учнями навичок і вмінь розв’язувати тригонометричні рівняння різними способами. Розвивати логічне мислення, навички самостійної роботи. Виховувати креатині здібності.

Тип уроку: урок засвоєння навичок і вмінь.

 

І. Актуалізація опорних знань.

Повторюємо відомі види тригонометричних рівнянь і способи їх розв’язання;

Формули подвійного кута ;

Формули пониження степеня…

ІІ. Ознайомлення учнів з висновками, що випливають в результаті розв’язання одного й того самого рівняння різними способами.

 

          Дано рівняння

Пропонуємо одній групі самостійно розв’язати це рівняння, застосувавши формулу подвоєного аргументу;

другій – помноживши на ;

третій формули пониження степеня.

 

Після взаємної перевірки робимо висновок, що знайдені множини коренів рівняння в усіх варіантах однакові:

  

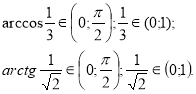
Отже, одержані арккосинус і арктангенс є радіанні міри гострих кутів прямокутних трикутників. Ці гострі кути рівні, якщо рівні їх значення тригонометричних функцій. Знайдемо значення будь-якої тригонометричної функції цих кутів, наприклад, тангенса.

- за змістом поняття арктангенса.

,

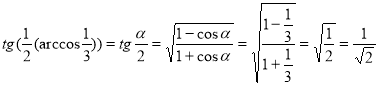Де число з інтервалом , косинус якого дорівнює 1/3. Перед квадратним коренем ставимо знак плюс, бо . Отже,

Зауважимо, що при розв’язуванні одного і того самого рівняння різними способами відповіді можуть бути виражені в різних формах.

ІІІ. Тригонометричні рівняння виду

Розглянемо один із способів його розв’язання.

Колективна робота.

Застосувавши формули синуса й косинуса подвійного аргументу, дістанемо:

 

 якщо , то дістанемо:

 

Це однорідне рівняння другого степеня відносно синуса й косинуса ми вже вміємо розв’язувати.

 

           2 спосіб.

Зручно розв’язати рівняння за допомогою формул:

 

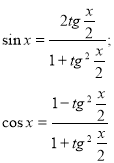
тоді дане рівняння зводиться до квадратного відносно треба пам’ятати, що при розв’язуванні таким способом можуть бути загублені розв’язки виду  , тому в дане рівняння  треба підставити , якщо отримаємо правильну рівність, тоді до відповіді додамо розв’язки виду

3 спосіб.

Такі рівняння можна розв’язувати введенням допоміжного кута. Нехай тому рівносильне йому рівняння:

  оскільки

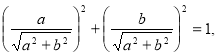  то існує такий кут , для якого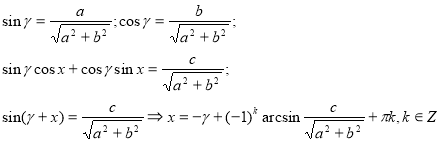

IV. Застосуємо ці міркування до конкретної вправи

 

 

V. Домашнє завдання. Ст.110-115 (розглянути різні способи розв’язування рівняння   );

Розв’язати рівняння №2(1, 8, 20, 28).

VI. Підсумок уроку.