Урок "Теорема Вієта і її застосування при розв'язуванні задач"
формувати вміння і навички в розв'язуванні завдань на застосування теореми Вієта; розвивати логічне мислення, пам'ять, зосередженість; виховувати наполегливість, кмітливість інтерес до вивчення математики; розвивати культуру математичного мовлення.
Алгебра 8 клас
Тема: Теорема Вієта і її застосування при розв’язуванні задач.
Мета уроку: формувати вміння і навички в розв’язуванні завдань на застосування теореми Вієта; розвивати логічне мислення, пам’ять, зосередженість; виховувати наполегливість, кмітливість інтерес до вивчення математики; розвивати культуру математичного мовлення.
Тип уроку: формування і вдосконалення вмінь та навичок
Обладнання: дошка, крейда, роздатковий матеріал.
Хід уроку
І. Організаційний момент
ІІ. Перевірка наявності домашнього завдання
ІІІ. Актуалізація опорних знань
- Сформулювати теорему Вієта. Розв’язати усно:
а) знайти суму і добуток коренів рівняння, якщо![]()
![]()
![]()
![]()
б) Сформулювати теорему Вієта для рівняння ![]()
Не раз в віршах оспівана, в сонетах,
Теорема коренів відомого Вієта.
І краще не знайти нічого,
Помножиш корені і дріб готовий.
В числівнику ![]()
![]()
І сума коренів теж дробом виступа,
Хай дріб із мінусом, але це не біда,
В числівнику ![]()
![]()
Застосувати теорему для рівнянь:
![]()
![]()
![]()
- Сформулювати обернену теорему Вієта
Виконати перевірку застосувавши обернену теорему Вієта:
![]()
![]()
![]()
![]()
![]()
![]()
-
Один із коренів рівняння
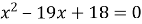 дорівнює 1. Знайти другий корінь.
дорівнює 1. Знайти другий корінь.
-
Один із коренів рівняння
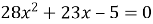 дорівнює -1. Знайти другий корінь.
дорівнює -1. Знайти другий корінь.
- Не розв’язуючи рівняння, визначити знаки його коренів (якщо вони є)
![]()
![]()
![]()
![]()
- Скласти зведене квадратне рівняння, коренями якого є числа:
а) ![]() б)
б) ![]()
![]()
![]()
-
Один із коренів рівняння
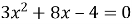 додатній, не розв'язуючи рівняння, визначити знак другого кореня.
додатній, не розв'язуючи рівняння, визначити знак другого кореня.
ІV. Розв’язування задач на застосування т. Вієта.
-
Різниця коренів квадратного
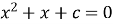 дорівнює 6. Знайти
дорівнює 6. Знайти 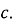
![]()
![]()
![]()
![]()
![]()
![]()
-
Не розв’язуючи рівняння
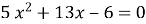 , знайдіть суму квадратів його коренів.
, знайдіть суму квадратів його коренів.
За теоремою Вієта: 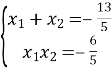
Так як ![]() , маємо:
, маємо:
![]()
-
Один із коренів рівняння
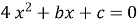 дорівнює 0,5, а другий – вільному коефіцієнту. Знайти
дорівнює 0,5, а другий – вільному коефіцієнту. Знайти 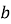
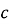
За теоремою Вієта: ![]()
![]()
![]()
![]()
![]()
![]()
-
Відомо, що
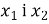 - корені рівняння
- корені рівняння 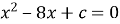 , причому
, причому
![]() , знайти
, знайти ![]()
Застосовуючи теорему Вієта маємо:
![]() ;
; ![]() ;
; ![]()
Значить ![]()
-
При якому значенні
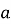

![]() , дорівнює 9?
, дорівнює 9?
![]()
За теоремою Вієта:
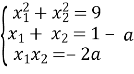
![]()
![]()
![]()
![]()
![]() +2
+2![]()
![]() ;
; ![]()
Перевірка:
-
При
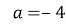
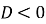
-
При
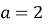
Відповідь: ![]()
-
Знайти суму кубів коренів рівняння
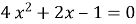 .
.
![]()
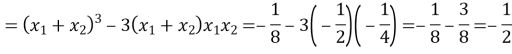
-
В рівнянні
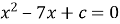 квадрат різниці коренів дорівнює 13. Знайти
квадрат різниці коренів дорівнює 13. Знайти 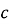
За теоремою вієта: 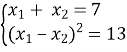 ;
; 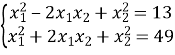
![]()
![]() Отже
Отже ![]()
-
При якому значенні
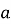
![]() приймає найменше значення?
приймає найменше значення?
За теоремою Вієта: ![]() маємо:
маємо:
![]()
![]()
![]()
Відповідь найменше значення при ![]()
-
При якому додатньому значенні
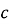
![]() дорівнює квадрату другого?
дорівнює квадрату другого?
![]() , за умовою
, за умовою ![]()
За теоремою Вієта 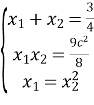
![]()
![]()
![]()
![]()
![]() Отже:
Отже:
![]()
![]() Тоді:
Тоді:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() не задовольняє умові задачі. Або
не задовольняє умові задачі. Або
![]()
![]()
Відповідь: ![]()
V. Підсумок уроку. Домашнє завдання: (за підручником Г.П. Бевз Алгебра7-8)
Повторити: Параграф: 40-42
Розв’язати: Б: №417, №420(а), №422(б)
В: №44, №45 (за збірником олімпіад них завдань
О.Біляніна, стор 21)


про публікацію авторської розробки
Додати розробку
