урок "Квадратні рівняння"

ТЕМА: Узагальнення та систематизація знань з теми «Квадратні рівняння»

МЕТА: закріпити і поглибити знання з теми, розвивати інтерес учнів до розв’язування вправ і задач; формувати вміння і навички самоперевірки і взаємоконтролю знань і вмінь.

ТИП УРОКУ: Узагальнення і систематизація знань.

ХІД УРОКУ

Коротке слово вчителя. Привітання. Пояснення, щодо ходу уроку. Сьогодні я хочу вас запросити в чудову захоплюючу мандрівку країною «Квадратних рівнянь». Ми подорожуватимемо «Математичним експресом», зупиняючись на станціях, зазначених в нашому маршрутному листі. Щоб опинитися в експресі треба придбати квиток, причому плата за квиток буде не в гривнях, а у ваших знаннях.

Актуалізація опорних знань.

1. Сформулюйте означення квадратного рівняння?
2. Які рівняння називаються неповними квадратними рівняннями?
3. Скільки коренів може мати квадратне рівняння?
4. Яке квадратне рівняння називається зведеним?
5. Від чого залежить розв’язок квадратного рівняння?
6. Скільки видів неповних квадратних  рівнянь ви знаєте?
7. Сформулюйте теорему Вієта?
8. Скажіть формули коренів квадратного рівняння?
9. Наведіть приклад зведеного квадратного рівняння?
10. Яка формула дискримінанта?
11. Наведіть приклади неповних квадратних рівнянь?
12. Як називається повне квадратне рівняння, в якому а=1?
13. Як із повного квадратного рівняння отримати зведене?
14. Сформулюйте обернену теорему Вієта?

Молодці, справилися із завданням і всі маєте право проїзду в нашому експресі.

Поділимось на туристичні групи (команди).

Учитель пояснює, як учень може провести самооцінку за таблицею оцінювання:

ІІ. Усна вправа (1)

Визначити тривалість подорожі, якщо вона дорівнює сумі коефіцієнтів квадратного рівняння  (у хвилинах)

І команда х² +8х+52=0

ІІ команда  -4х² +27х+22=0

ІІІ команда 100х² –х-54=0

Відповідь 45 хвилин

Кожна із наших туристичних груп визначила тривалість подорожі, а, отже, має право подорожувати.

Під час руху поїзда.

Дозволяється:

• Виявити кмітливість, знання;
• Мати почуття гумору
• Допомагати своїм друзям
• Мати гарну і добре організовану

Забороняється:

• Перевозити з собою шпаргалки, прилади, які знищує інтелект.

Що ж щасливо! Успіху Вам!

Наш математичний експрес прибуває на станцію «Неповні квадратні рівняння»

Завдання 2 . Які із рівнянь

1. 7х² +3=0
2.  х² -5х=0
3. х² +4=0
4. 7х² -28=0
5. 3х² =0
6. -5х² =20

І команда не має коренів

ІІ команда  має один корінь

ІІІ команда  має два корені

Завдання 3 . Знайти корені квадратного рівняння:

І команда  2х+5х² =0

1. 0
2. 0;-0,4
3. 0;0,4
4. -0,4;0,4

ІІ команда

 2х² -50=0

1. 0;25
2. 5;0
3. 5
4. -5;5

ІІІ команда

 6х² =18

1. 3;-3
2. 
3. ;
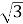
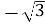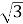
4. 0;3

Із станції «Неповні квадратні рівняння» ми направляємось до станції «Дискримінант»

На станції нас чекають завдання; розв’язати які ви зможете, пригадавши формули дискримінанта та коренів квадратного рівняння. Нам запропонували шпаргалку, але чи можемо ми довіряти, тому що в ній написано, перевіримо.

Завдання 4. Хто бажає виправити помилки

І команда. Перевірити чи правильно записана формула дискримінанта. Якщо є помилки то виправити їх: D=b-4ac

ІІ команда Перевірити чи правильно записана формула

ІІІ команда Перевірити чи правильно записана формула

Пропоную застосувати отримані формули для розв’язування  квадратних рівнянь

Завдання 5. Хто бажає виправити помилки.

І команда 7х² -6х-1=0

ІІ команда  2х² +5х+3=0

ІІІ команда 2х² -5х-3=0

Прошу команди направити до дошки одного представника.

Решту члени команди працюють на місцях.

Звірте результати із записаними на дошці прошу виправити.

Наступна наша зупинка на  станції «Теорема Вієта»

Завдання 6. Не розв’язуючи рівняння, знайти суму і добуток його коренів

І команда

1. х² -9х+1=0
2. 3х² -5х-7=0
3. х² -4х+5=0

ІІ команда 

1. х² +5х-3=0
2. 4х² -7х+1=0
3. 2х² +3х+2=0

ІІІ команда

1. х² +16х-3=0
2. -2х² +5х+6=0
3. х² +6х+10=0

Я не погоджуюсь з вами у випадку третього рівняння. Чому?  Ви здогадаєтесь, обчисливши дискримінант квадратного рівняння. D=16-20=-4<0. Розв’язків немає. Отже, ви завжди повинні обчислювати дискримінант, щоб переконатися чи рівняння має розв’язки, для того щоб знайти їхню суму і добуток.

Команда, яка є першою пояснить чому для третього рівняння не можна застосовувати теорему Вієта, тій команді плюс1 бал.

А зараз наш експрес на  станцію «Ерудит»

Тут вміють розв’язувати не лише квадратні рівняння, а й складніші завдання.

Завдання 7. Розв’язати  рівняння, які зводяться до квадратних.

І команда

(х-3)² =2(3х-1)   (1;11)

ІІ команда 

                   (-1;5)

ІІІ команда

(3z-1)(3z+1)+z=4z(2z+1)+27     (-4;7)

Знайдіть добуток всіх коренів цих рівнянь

 Х₁ х₂ y₁  y₂ z₁z₂=1540 (року)

Це число відповідає року народження Вієта.

Отже, його теорема і слова видатного математика живуть вже більше як 4 століття.

Під'їжджаємо до станціі «Практична»

Все, що ми вивчаємо цінне лише тоді, якщо ми знайдемо місце для його застосування в житті, на практиці.

Задача.

Для покриття підлоги в кімнаті прямокутної форми периметром 18м було закуплено паркет загальною площею 20 м². Чи можна в цій кімнаті вздовж однієї стіни розмістити стінку довжиною 4,8м?

Підсумок уроку.

1. Підрахуйте суму балів на маршрутному листку команди. Назвіть результати. Отже команда … набрала стільки балів…

Переможцем стала команда …

Дякую, що ви гарно працювали,

2. Ваші особисті маршрутні листки і зошити для перевірки і оцінювання прошу здати