Урок-лекція. Поняття про об’єм тіла. Основні властивості об’ємів. Об’єми паралелепіпеда, призми, піраміди, подібних тіл.

 

 

 

 

 

Навчальний модуль

 

Об’єми та площі поверхонь

геометричних тіл

 

 

 

Геометрія 11 клас

 

 

 

 

  Підготувала вчитель математики

Яблунського ліцею

Солотвинської селищної ради

 Костур Дарія Дмитрівна

 

 

 

 

 

Конспект №1

 

Урок-лекція (2 год)

 

Найкращий спосіб вивчити
що-небудь – відкрити
його самостійно.

Д. Пойа

 

 

Тема модуля.  Поняття про об’єм тіла. Основні властивості об’ємів. Об’єми паралелепіпеда, призми, піраміди, подібних тіл.

 

Мета модуля:  Сформулювати поняття об’єму тіла, рівновеликих тіл; домогтися засвоєння властивостей об’єму многогранників, формул для обчислення об’ємів паралелепіпеда, призми, піраміди, подібних тіл; сформувати вміння розв’язувати задачі на обчислення об’ємів многогранників; розвивати вміння сприймати просторові форми навколишнього світу; виховувати відповідальне і наполегливе ставлення до навчання, охайність, пізнавальну самостійність, розумову активність, потребу в самоосвіті.

 

Тип модуля:  установчо-мотиваційний.

 

Вид модуля:  лекція з поетапним закріпленням нового матеріалу.

 

Обладнання:  дошка, крейда, таблиця “Сьогодні на уроці”, моделі многогранників (прямокутного паралелепіпеда, прямої трикутної і многокутної призм, похилої призми, піраміди), підручник, міні-підручник, мультимедійна дошка.

 

Планіметричний матеріал:  площі фігур (прямокутника, паралелограма, трикутника, трапеції); властивості рівнобедреного трикутника; теорема Піфагора; співвідношення між сторонами і кутами прямокутного трикутника.

 

Комплексне застосування методів:  евристична бесіда, активні форми “Мікрофон”, “Мозковий штурм”, проектна технологія, проблемні ситуації.

Хід уроку

 

 

І. Організаційний момент.

 

1. Підготовка до сприйняття нової теми.

 

Перший міні-модуль. Установчо-мотиваційний.

 

Учитель. Сьогодні ми починаємо вивчення нового модуля «Об’єми та площі поверхонь геометричних тіл». На вивчення модуля відводиться 14 годин. Теоретичний матеріал буде поданий узагальнюючими модулями на лекціях. Розподіл навчальних годин на теоретичний матеріал і практичні заняття такий:

1.     Урок-лекція (2 год). Поняття про об’єм тіла. Основні властивості об’ємів. Об’єми паралелепіпеда, призми, піраміди, подібних тіл.
2.     Урок-практикум (2 год). Розв’язування базових задач. Самостійна робота.
3.     Урок-лекція (2 год.). Об’єми тіл обертання: циліндра, конуса, кулі та її частин.
4.     Урок-лекція (2 год.). Площі поверхонь тіл обертання.
5.     Урок-практикум (2 год.). Розв’язання типових задач. Самостійна робота.
6.     Урок-семінар (2 год.). Проект «Об’єми многогранників та тіл обертання. Площі поверхонь тіл обертання».
7.     Урок-контроль (2 год.). Контрольна робота.

 

 

2. Пам’ятка “Знати, вміти” (поміщена в математичному кабінеті на стенді “Сьогодні на уроці”).

Очікувані результати. Після вивчення теми учні повинні:

• мати уявлення про

• об’єм тіла;
• площу поверхні тіла;

• знати

• основні властивості об’ємів;
• формули для обчислення об’ємів паралелепіпеда, призми, піраміди, подібних тіл;

• уміти

• розв’язувати прості задачі на знаходження об’ємів та площ поверхонь зазначених у змісті програми тіл.

 

3. На початку вивчення модуля учні одержують домашню контрольну роботу, яка містить питання з теорії і задачі (захищати після вивчення модуля перед контрольною роботою).

 

 

4. Аркуш оцінок (учні заповнюють таблицю в процесі вивчення модуля).

 

С.р №1	С.р №2	К.р	Дом. завд.	Зошит	Усна відпов.	Прак. робота	Мат. дикт.	Дом. к.р.	Піл. бали	Міні-підручник	Заг.  сума у балах	Оцінка
10	10	12	6	5	5	5	6	8	6	6	79	12

 

Початковий рівень     

“1” – 20-24 бали,

“2” – 25-29 балів,

“3” – 30-34 бали

 

Середній рівень

“4” – 35-39 балів,

“5” – 40-44 бали,

“6” – 45-49 балів

 

Достатній рівень

“7” – 50-54 бали,

“8” – 55-59 балів,

“9” – 60-64 бали

 

Високий рівень

“10” – 65-69 балів,

“11” – 70-74 бали,

“12” – 75-79 балів

 

 

 

ІІ. Повідомлення теми, мети, орієнтованого плану лекції.

 

Перший міні-модуль. Змістово-пошуковий.

 

1. Поняття об’єму геометричного тіла.
2. Властивості об’єму многогранників.
3. Означення рівновеликих геометричних тіл.
4. Формули для обчислення об’ємів прямого паралелепіпеда, куба, похилого паралелепіпеда.
5. Приклади застосування формул для обчислення об’ємів куба та паралелепіпедів.

 

Другий міні-модуль. Змістово-пошуковий.

 

1. Формули для обчислення об’ємів прямої та похилої призм.
2. Приклади застосування формул для обчислення об’ємів призм.

 

Третій міні-модуль. Змістово-пошуковий.

 

1. Формули для обчислення об’єму піраміди.
2. Об’єми подібних тіл.
3. Приклади застосування формул для обчислення об’єму піраміди.

 

 

ІІІ. Цілепокладання.

 

Ви вже знаєте тему, мету уроку. Чого очікуєте від уроку? Які завдання ставите перед собою на цьому уроці? (Кожен учень отримує карточку і записує очікувані результати одним реченням, разом вибираємо найтиповіші і записуємо на дошці).

 

 

IV. Вивчення нового матеріалу.

 

Сприймання і усвідомлення нового матеріалу.

 

1.   Робота з підручником [5] (задачу про вимірювання об’ємів многогранників розглядаємо по аналогії із задачею про вимірювання площ многокутників)

Запитання

1. Яке тіло називається простим?
2. Що таке об’єм?
3. Сформулювати основні властивості об’єму.
4. Що таке одиничний куб?

 

2.   Клас об’єднано в три групи: «Паралелепіпед», «Призма», «Піраміда». Кожна група готувала презентацію відповідно до своєї назви.

 

Презентація кожної з груп (учні самостійно, працюючи з підручником, з’ясовують формули для обчислення об’ємів паралелепіпеда, призми, піраміди).

 

 

3.   У міні-підручниках учні записують довідник формул.

 

Об’єми многогранників

(a, b, c – лінійні виміри) – об’єм прямокутного паралелепіпеда

– об’єм будь-якого паралелепіпеда

– об’єм будь-якої призми

– об’єм похилої призми, де – площа перерізу, перпендикулярного до бічних ребер, – довжина бічного ребра (задача-теорема)

– об’єм піраміди

– об’єм зрізаної піраміди, де H – висота піраміди, Q₁, Q₂ – площі основ

Об’єми двох подібних тіл відносяться, як куби їх відповідних лінійних розмірів.

 

 

4.   Кожна група отримує картку з текстом задачі, яку треба розв’язати упродовж 5 хв. Усі задачі різні.

За допомогою мультимедійного проектора задачі проектую на дошку.

 

 

 

Задача для групи «Паралелепіпед»

Сторона основи правильної чотирикутної піраміди дорівнює 5 см, а висота піраміди – 15 см. Знайти об’єм піраміди.

 

 

 

 

 

 

 

 

 

 

 

 

 

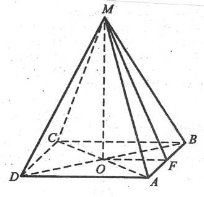
Задача для групи «Призма»

Основою прямокутного паралелепіпеда є квадрат. Діагональ бічної грані паралелепіпеда дорівнює 8 см і утворює з площиною основи кут 30^о. Знайти об’єм паралелепіпеда.

 

 

 

 

 

 

 

 

 

 

 

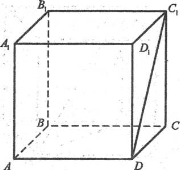
Задача для групи «Піраміда»

Основа прямої призми – рівнобедрений трикутник з основою 5 см і висотою, проведеною до неї, 6 см. Знайти об’єм призми, якщо її бічне ребро дорівнює 8 см.

 

 

 

 

 

 

 

 

 

 

 

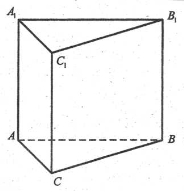
Відтворити готове розв’язання задачі.

 

Задача. У прямокутному паралелепіпеді кут між діагоналями основи дорівнює α. Діагональ однієї з бічних граней утворює з площиною основи кут β. Знайти об’єм прямокутного паралелепіпеда, якщо його висота дорівнює а.

 

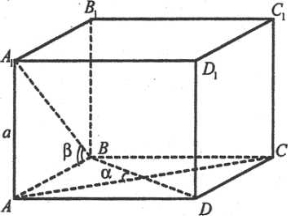
Розв’язання

Нехай основою прямокутного паралелепіпеда є прямокутник ABCD,   О – точка перетину діагоналей основи.

За умовою АОВ=α. Протилежними бічними гранями є рівні прямокутники, діагоналі яких рівні.

Розглянемо діагональ А₁В грані АА₁В₁В. Оскільки АА₁(АВС), то проекцією діагоналі А₁В на площину основи є сторона АВ. Тому кут А₁ВА – кут нахилу діагоналі А₁В до площини основи, за умовою А₁ВА=β, АА₁=а.

З трикутника АА₁В (А₁АВ=90^о):

Діагоналі прямокутника АВСD рівні і точкою перетину діляться навпіл. Тому ОА=ОВ і маємо:

З трикутника АВD(BAD=90^o):

Отже, об’єм паралелепіпеда

 

Для закріплення нового матеріалу розв’язати задачі і вправи №№1113-1120, 1151, 1153, 1154 з підручника [6] усно.

 

 

 

V. Рефлексія уроку, використовуючи прийом «Незакінчені речення».

 

Я сьогодні на уроці  дізнався…

Повторив…

Навчився…

Зрозумів…

Зробив успіхи…

Навчив інших…

Відчув труднощі…

Я не знав, а тепер знаю…

Я не вмів, а тепер вмію…

Було найцікавіше працювати над…

Мої побажання щодо наступних занять…

Відчув плече друга, коли…

 

 

Домашнє завдання.

1. За підручником [5]: вивчити теоретичний матеріал §7, п.п. 65-71; дати відповіді на запитання 1-9 (с. 108); розв’язати задачі №№25, 33, (с. 110-111).
2. Повторити: п.п. 67-70 (8 клас), 103-106 (9 клас) (підручник [7]).

 

 

 

 

 

 

Література

 

1. Пєхота О.М. Сучасні освітні технології. – К., А.С.К., 2001.
2. Смишляєва В.К. У світі математики. – К.; Рад. шк., 1976. – Випуск   7. – с. 183.
3. Пометун О., Пироженко Л. Сучасний урок. – К.: А.С.К., 2003.
4. Істер О.С., Глобін І.Є., Панкратова І.Є. Збірник завдань для державної підсумкової атестації з математики. – Київ.: ЦНМЛ, 2011.
5. Погорєлов О.В. Геометрія: Стереометрія: Підруч. Для 10-11 кл. серед. шк. К.: Освіта, 1998.
6. Бевз Г.П., Бевз В.Г., Владімірова Н.Г., Владіміров В.М. Геометрія: Стереометрія: Підруч. Для 11 кл загальноосвітніх навчальних закладів. – К.: «Генеза», 2011.
7. Погорєлов О.В. Геометрія: Планіметрія: Підручник для 7-9 кл. загальноосвітніх навчальних закладів. – К.: Школяр, 2004.