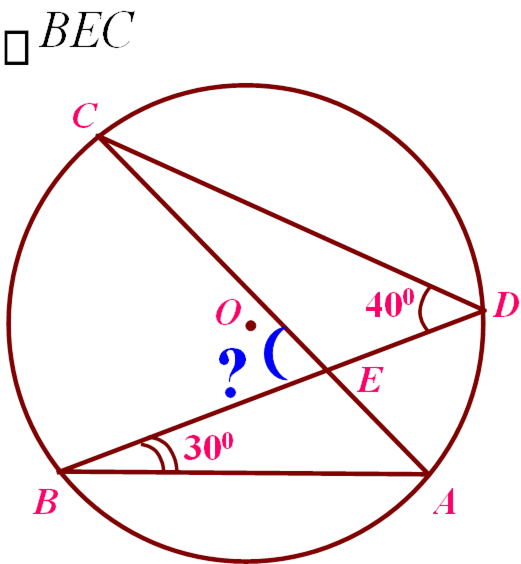
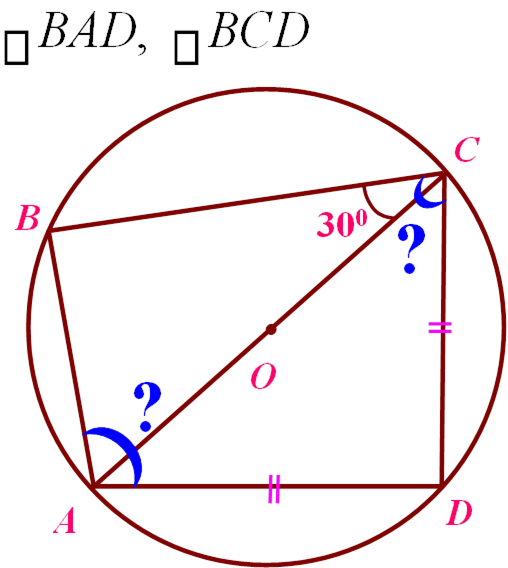
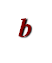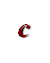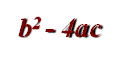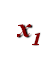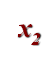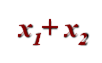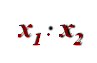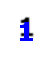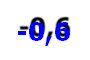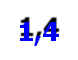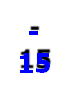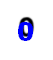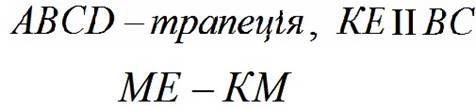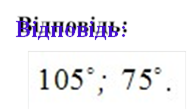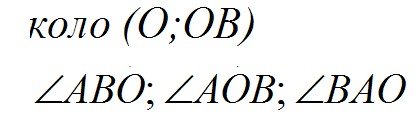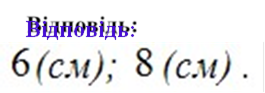Презентація Майстер-клас "Я це роблю так..."
 |
 |

 |

ІННОВАЦІЙНІ ТЕХНОЛОГІЇ НАВЧАННЯ
1. РОЗВИТОК КРИТИЧНОГО МИСЛЕННЯ - система діяльності, що базується на дослідженні проблем та ситуацій на основі самостійного вибору, оцінки та визначення міри корисності інформації відносно особистих потреб і цілей.
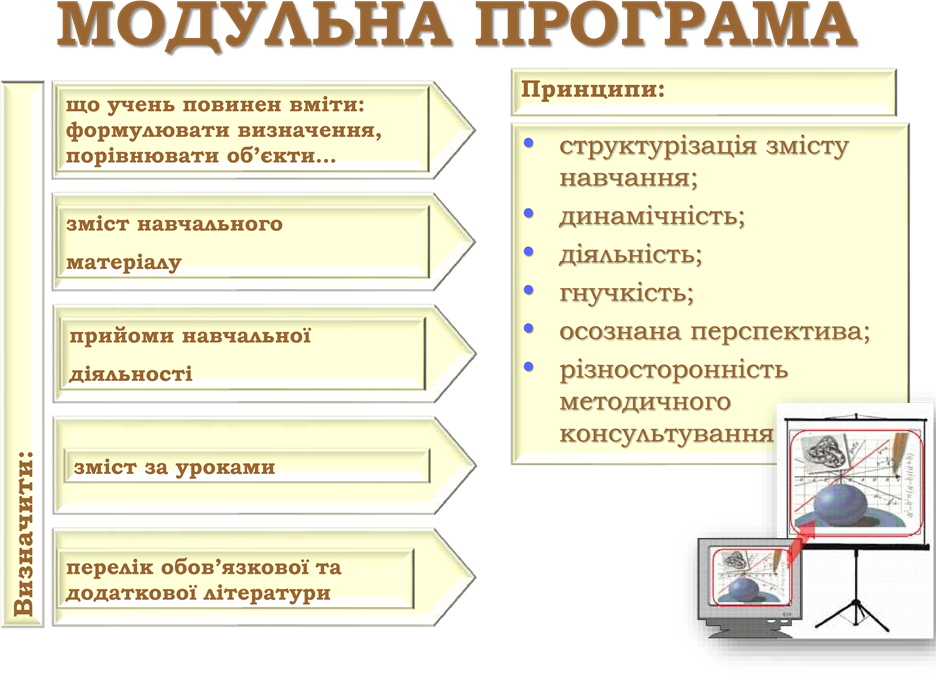
2.  МОДУЛЬНО-РОЗВИВАЛЬНЕ НАВЧАННЯ Основне завдання – формування самоосвітньої компетентності учнів. Основний структурний елемент є модуль (від лат. Modulus – “міра”) – самостійний, функціональноорієнтований етап процесу навчання, що має власне програмно – цільове та методичне забезпечення.
МОДУЛЬНО-РОЗВИВАЛЬНЕ НАВЧАННЯ Основне завдання – формування самоосвітньої компетентності учнів. Основний структурний елемент є модуль (від лат. Modulus – “міра”) – самостійний, функціональноорієнтований етап процесу навчання, що має власне програмно – цільове та методичне забезпечення.
3.  МЕТОД ПРОЕКТІВ - це спільна навчально-пізнавальна творча або ігрова діяльність учнів–партнерів, яка має спільну мету – дослідження деякої проблеми, узгоджені методи, способи діяльності, направлена на досягнення спільного результату діяльності.
МЕТОД ПРОЕКТІВ - це спільна навчально-пізнавальна творча або ігрова діяльність учнів–партнерів, яка має спільну мету – дослідження деякої проблеми, узгоджені методи, способи діяльності, направлена на досягнення спільного результату діяльності.
4. ІНФОРМАЦІЙНІ ТЕХНОЛОГІЇ Використання комп’ютерних технологій та програмного забезпечення під час уроків математики
5.  ІНТЕРАКТИВНЕ НАВЧАННЯ створити комфортні умови навчання, за яких кожен учень відчуває свою успішність, інтелектуальну спроможність. Слово “інтерактив” походить від англійського “interact” (“inter” – взаємний і “act” –діяти ). Інтерактивний – здатний до діалогу , взаємодії.
ІНТЕРАКТИВНЕ НАВЧАННЯ створити комфортні умови навчання, за яких кожен учень відчуває свою успішність, інтелектуальну спроможність. Слово “інтерактив” походить від англійського “interact” (“inter” – взаємний і “act” –діяти ). Інтерактивний – здатний до діалогу , взаємодії.
 |
МЕТОД «ПРЕС»
Дана технологія відкриває можливості доводити, висловлювати свої думки, обґрунтовувати свої міркування за певним алгоритмом: «Я вважаю, що...», «тому що...», «наприклад..», «отже, я вважаю...»
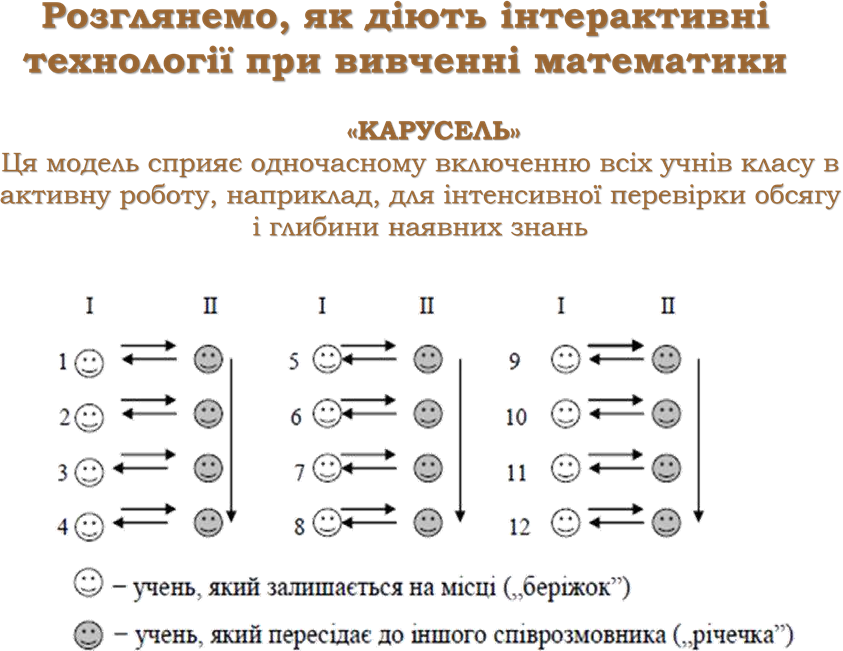
МЕТОД «КАРУСЕЛЬ»
 Учні сідають у два кола – внутрішнє і зовнішнє. Внутрішнє коло нерухоме, зовнішнє рухається. Можливі два варіанти використання методу – для дискусії (відбуваються “попарні суперечки” кожного з кожним, причому кожен учасник внутрішнього кола має власні, неповторювані докази), чи для обміну інформацією (учні із зовнішнього кола, рухаючись, збирають дані).
Учні сідають у два кола – внутрішнє і зовнішнє. Внутрішнє коло нерухоме, зовнішнє рухається. Можливі два варіанти використання методу – для дискусії (відбуваються “попарні суперечки” кожного з кожним, причому кожен учасник внутрішнього кола має власні, неповторювані докази), чи для обміну інформацією (учні із зовнішнього кола, рухаючись, збирають дані).
МЕТОД «МОЗКОВИЙ ШТУРМ»
Загальновідома технологія, суть якої полягає в тому, що всі учні по черзі висловлюють абсолютно всі, навіть алогічні думки з приводу проблеми. Висловлене не критикується і не обговорюється до закінчення висловлювань.
КУРІННА ВЕРОНІКА АНАТОЛІЇВНА
 |



 |
 |

 |
СЮЖЕТНІ ЗАДАЧІ, ПОВ’ЯЗАНІ З ЖИТТЄВИМИ СИТУАЦІЯМИ
Тюльпан гранітний – квітка Запорізького краю, яка через недбайливе ставлення людей, була занесена до Червоної книги України. Але останнім часом ми почали більше любити навколишній світ, тому кількість квітів почала збільшуватись.
Задача. На березі Дніпра першого дня травня розцвіло 7 тюльпанів, а другого – в 3 рази більше. Скільки тюльпанів розцвіло за два дні?
Морква – корисний овоч, до її складу входить вітамін А (каротин), який поліпшує зір. Краще моркву споживати, змастивши жиром (олія, сметана), а сік з неї випивати протягом години.
 Задача. Після того, як на консервному заводі вичавили сік з з40 кг моркви, там залишилося ще 655 кг моркви. Скільки кілограмів моркви було на консервному заводі спочатку?
Задача. Після того, як на консервному заводі вичавили сік з з40 кг моркви, там залишилося ще 655 кг моркви. Скільки кілограмів моркви було на консервному заводі спочатку?
 |


 |
ВИВЧЕННЯ НОВОГО
МАТЕРІАЛУ
Вводне повторення Уроки-практикуми
у формі бесіди, в якій учні концентрують в Форма роботи пам’яті знання, необхідні для вивчення
нового матеріалу • Групова
 Лекція-практикум • Співробітництво по принципу оберненого зв’язку, що дозволяє• Інтерес передати учням знання та направити їх на
Лекція-практикум • Співробітництво по принципу оберненого зв’язку, що дозволяє• Інтерес передати учням знання та направити їх на
пошук нових знань Контроль
• Вхідний контроль
Тренінг-мінімум • Проміжковий мета - автоматизація вмінь розв’язувати зрізовий,
стандартні задачі корегуючий
• Залік практичний
Систематизація вивченого
та теоретичний мета – концентрація необхідних знань
• Підсумковий для розв’язування завдань
вихідний контроль
 |

 |
 |
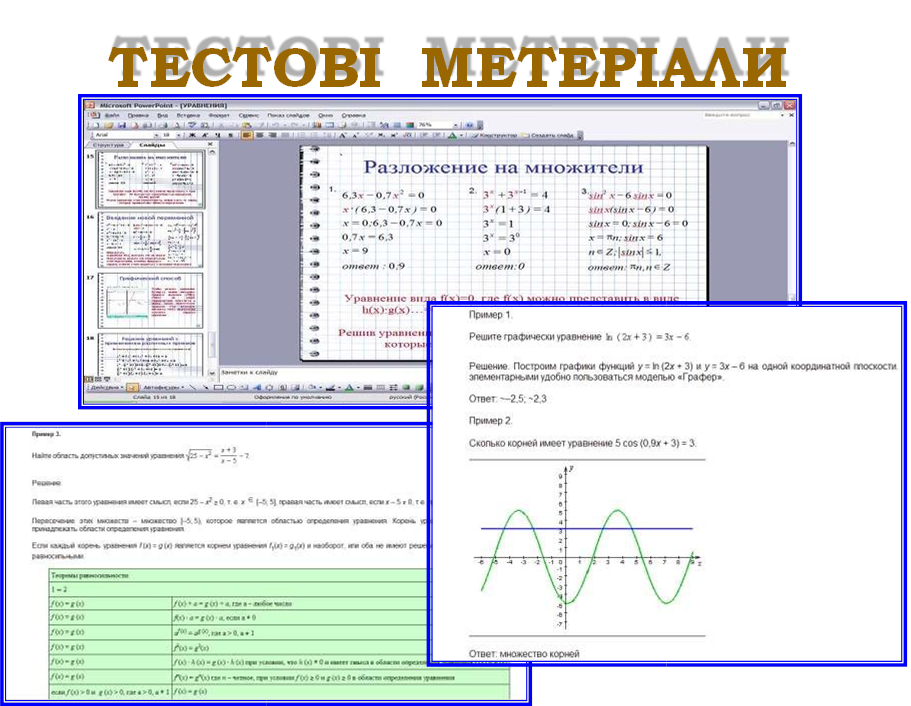 |
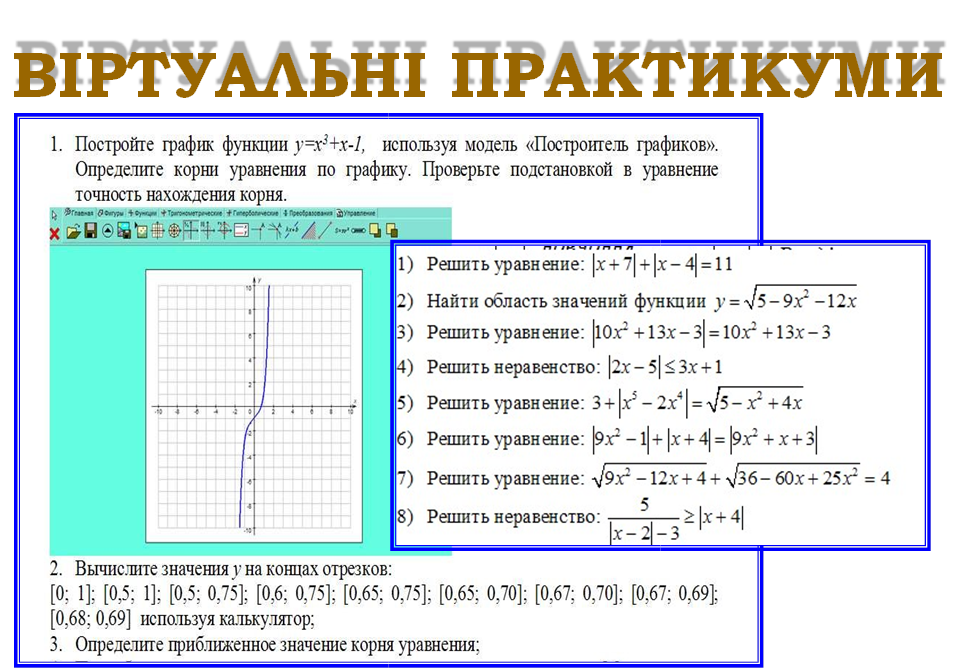
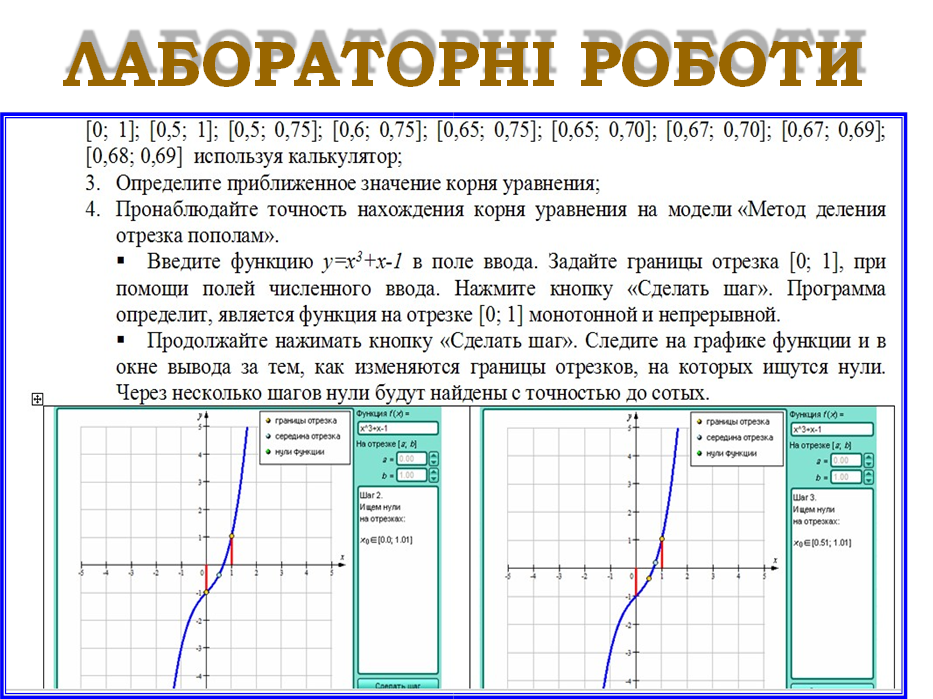 |
 |
 |
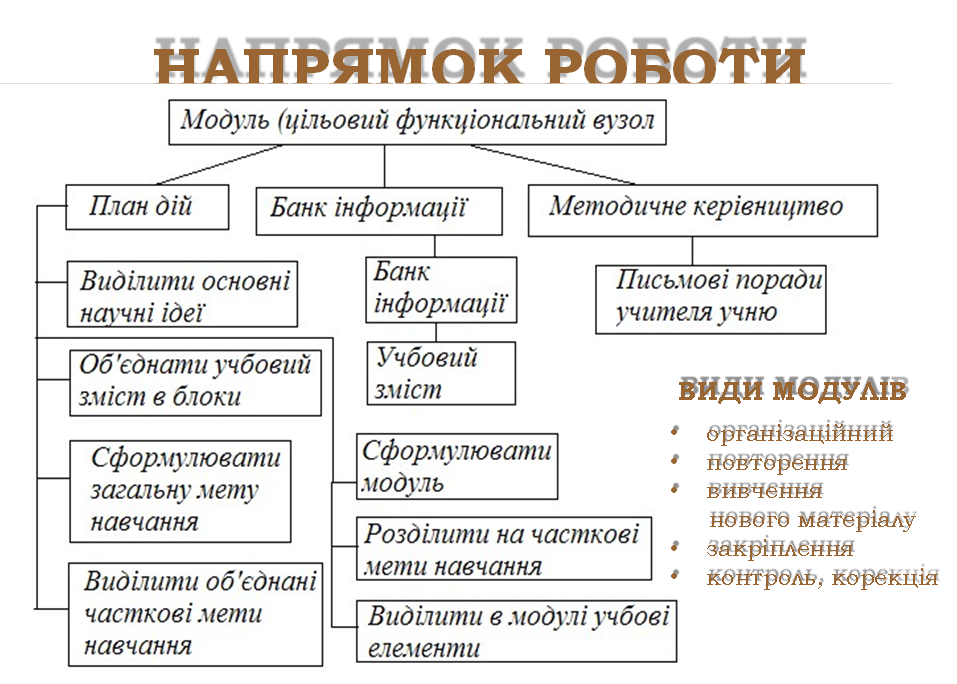
ТРУДНОЩІ У РЕКОМЕНДАЦІЇ
ВИКОРИСТАННІ
Програми, використання учнями
МОДУЛЬНОЇ ТЕХНОЛОГІЇ інтерактивних форм та методів для
самоосвіти та корекції знань
Здатність учнів працювати
самостійно з навчальною 1С: освіта створення інформацією свого банку
тестових завдань використання
Різний рівень підготовки учнів та
здатність раціонально on-line тестів
організувати свою роботу створення
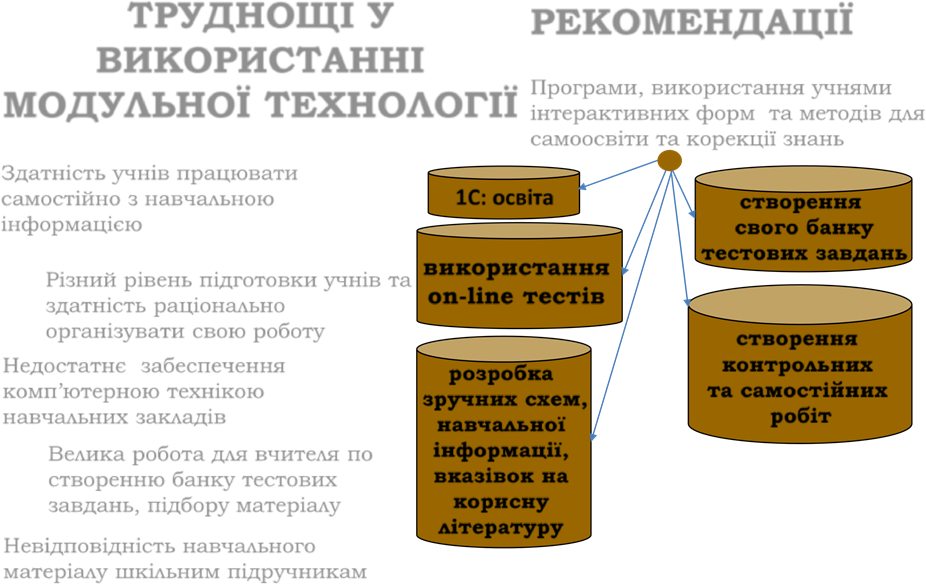 Недостатнє забеспечення розробка контрольних комп’ютерною технікою зручних схем, та самостійних навчальних закладів навчальної робіт
Недостатнє забеспечення розробка контрольних комп’ютерною технікою зручних схем, та самостійних навчальних закладів навчальної робіт
Велика робота для вчителя по інформації, створенню банку тестових вказівок на
завдань, підбору матеріалу корисну
літературу
Невідповідність навчального матеріалу шкільним підручникам




 |

 |
 |

 |
|
6 у= х |
В яких чвертях
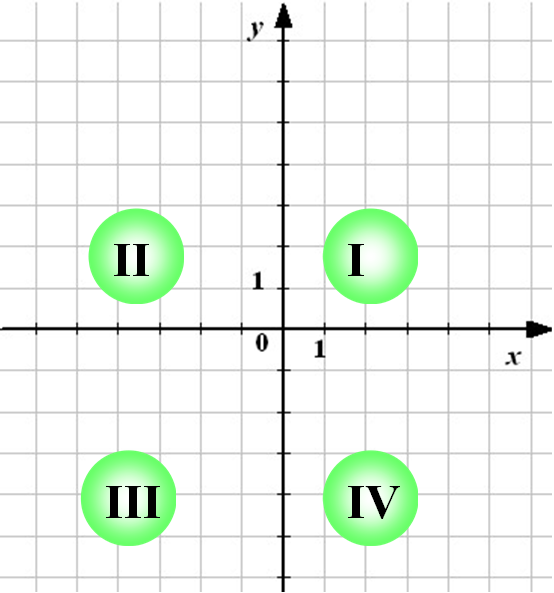 Розташовано графік:
Розташовано графік:
|
6 у= х |
В яких чвертях
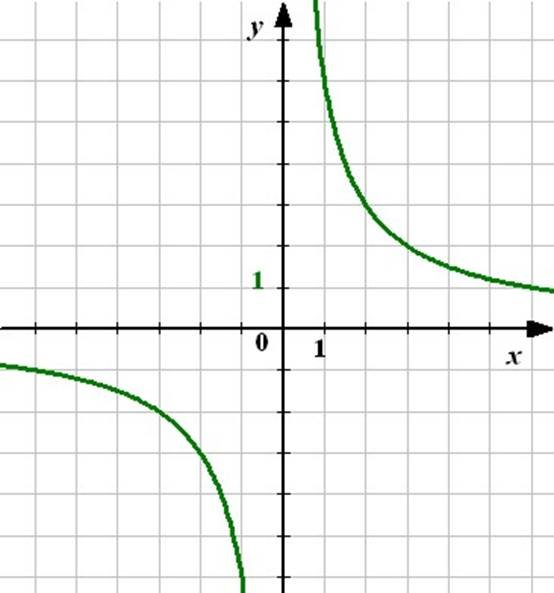 Розташовано графік:
Розташовано графік:
|
4 у=− х |
![]() В яких чвертях розташовано графік
В яких чвертях розташовано графік
|
4 у=− х |
![]() В яких чвертях розташовано графік
В яких чвертях розташовано графік
|
у= 0,5х2 |
![]() В яких чвертях розташовано графік:
В яких чвертях розташовано графік:
|
у= 0,5х2 |
![]() В яких чвертях розташовано графік:
В яких чвертях розташовано графік:
|
|
![]() В яких чвертях розташовано графік:
В яких чвертях розташовано графік:
|
|
![]() В яких чвертях розташовано графік:
В яких чвертях розташовано графік:
|
у=х3 |
![]() В яких чвертях розташовано графік:
В яких чвертях розташовано графік:
|
у=х3 |
![]() В яких чвертях розташовано графік:
В яких чвертях розташовано графік:
Розв’язати графічно рівняння:
|
х |
у |
|
- 3 |
0 |
|
0 |
3 |
х+3 = 5−х
у = у =
![]() Визначити, яке рівняння розв’язано:
Визначити, яке рівняння розв’язано:
![]() Визначити, яке рівняння розв’язано:
Визначити, яке рівняння розв’язано:
![]()

![]()
![]() Приклади квадратних рівнянь:
Приклади квадратних рівнянь:
а) –х²+6х+1,2=0, де а=-1, в=6, с=1,2;
б) 5х²-2=0 – неповне квадратне
рівняння, де а=5, в=0, с=-2;
в) -3х²+7х=0 - неповне квадратне
рівняння, де а=-3, в=7, с=0;
г) 7х²=0 - неповне квадратне
рівняння, де а=7, в=0, с=0;
д) х²+4х-12=0 – зведене квадратне рівняння, де а=1, в=4, с=-12.

 Приклади розв’язування квадратних рівнянь за Приклад: формулою
Приклади розв’язування квадратних рівнянь за Приклад: формулою
3x2 +11x + 6 = 0 a = 3;b =11;c = 6
D =112 − 436 =121−72 = 49 0, ð³âí ÿí í ÿ ì ຠäâà êî ðåí ³
õ1,2 =  = õ1 =
= õ1 = 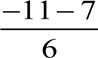 = −3;
= −3;
õ2 = ![]() −11+ 7 = −
−11+ 7 = − ![]() 2
2
6 3
³äï î â³äü: 3− ;−![]() .
.
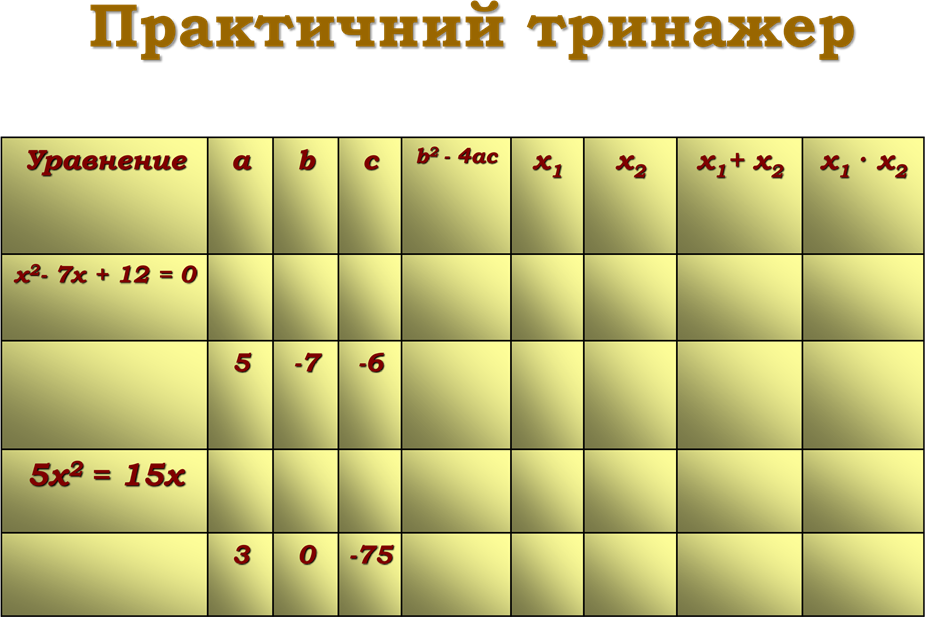
![]() Практичний тринажер
Практичний тринажер
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Завдання 1. Розв’яжіть рівняння:
|
х2 −5х+6
|
х=2
|
х2 −х−6
|
х=3
|
х2 −х−6
|
х=3

ах2 +bх+c=0
|
Алгоритм: |
ах2 +bх+c=0
![]() а0
а0![]() ах2 +bх+c=0 х2 +
ах2 +bх+c=0 х2 +![]() bх+
bх+![]() c =0 a a
c =0 a a
у = у =
у = х2
![]() Парабола.
Парабола.
Вітки до верху. у = 4
Метод виділення квадрату двочлена
![]() Мета: привести квадратне рівняння загального виду до неповного квадратного рівняння
Мета: привести квадратне рівняння загального виду до неповного квадратного рівняння
x2 −6x+ =8 0 Приклад:
(x−3)2 − =1 0
x− =3 1,
x− =−3 1.
 Метод «перекиду» найвищого коефіцієнту
Метод «перекиду» найвищого коефіцієнту
Корні квадратних рівнянь
ax2 +bx+c=0 та y2 +by+ac=0
![]() пов’язані співвідношеннями y1 x2 = y2
пов’язані співвідношеннями y1 x2 = y2
x1 = a та a
2x2 − − =9x 5 0 z2 − − =9z 10 0
z1 =10;z2 =−1
1 1
x1 = 5;x2 =− ![]() . ³äï î â³äü:−
. ³äï î â³äü:− ![]() ;5
;5
5 5
На основі теорем:
![]() ❖Якщо в квадратному рівнянні a+b+c=0, то один з коренів дорівнює
❖Якщо в квадратному рівнянні a+b+c=0, то один з коренів дорівнює
1, а другий за теоремою Вієта дорівнює c
a
❖Якщо в квадратному рівнянні a+c=b,
то один з коренів дорівнює -1,
c а другий за теоремою Вієта дорівнює− ![]() a
a
![]() Приклади: 157x2 +20x−177 0=
Приклади: 157x2 +20x−177 0=
203x2 +220x+ =17 0
|
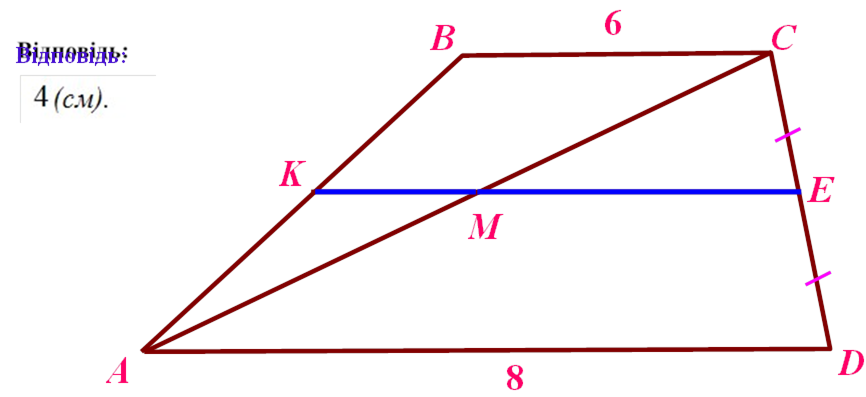
Знайти: |
PAÌÑÊ , SAMCK
 C
C
A D
|
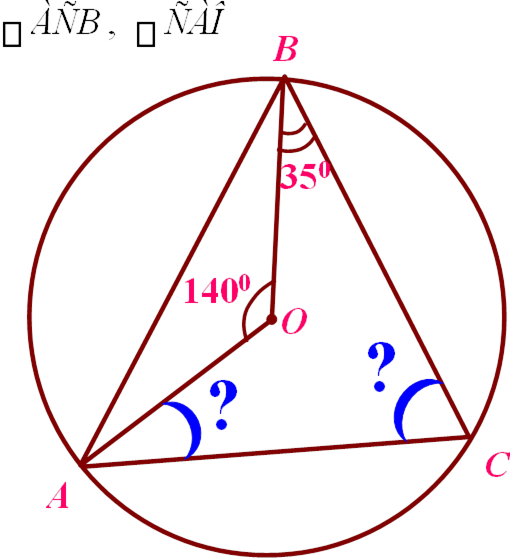
Знайти: |
PAÎÂ , SAÎÂ
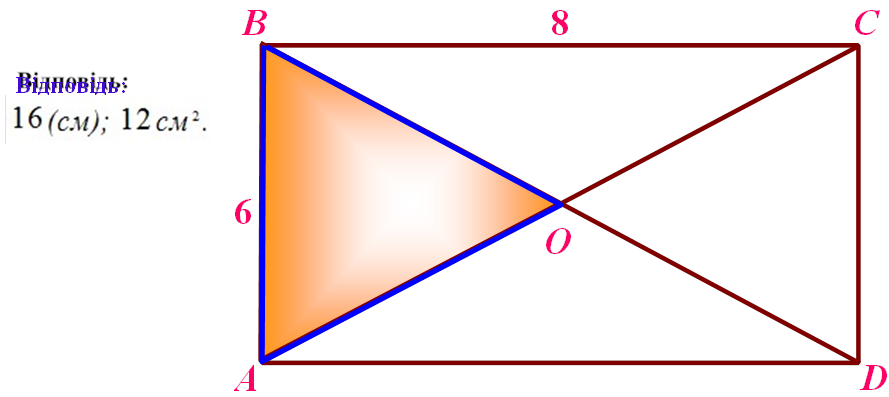
AÂ=8, ÀÊ : ÀÂ=3:8, ÑÐ:CD=3:8
|
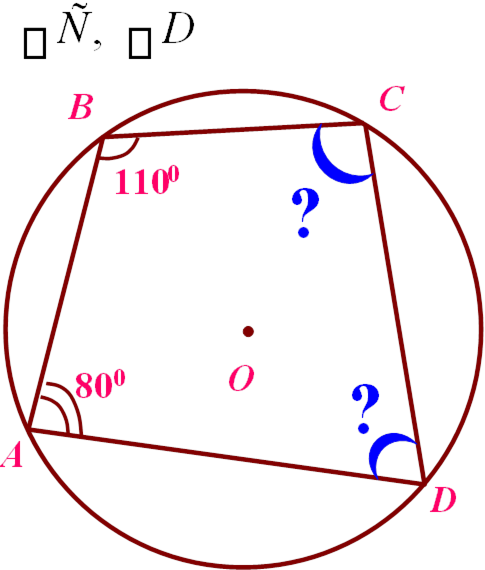
Знайти: |
PDKPÂ, SDKPÂ
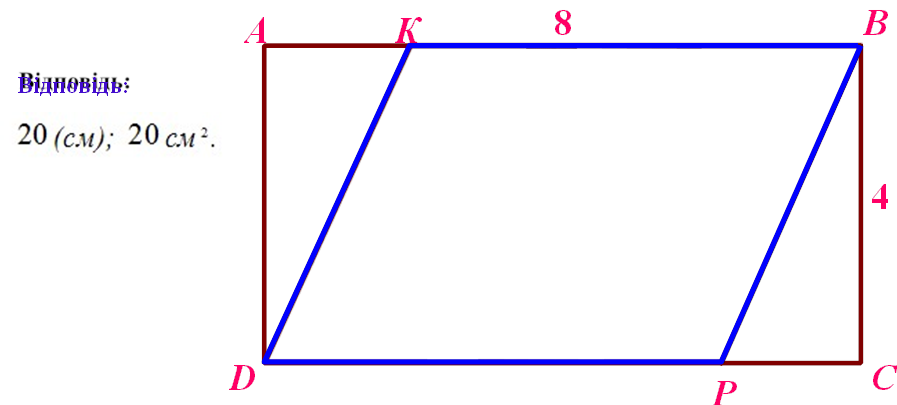
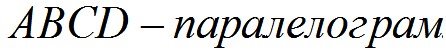
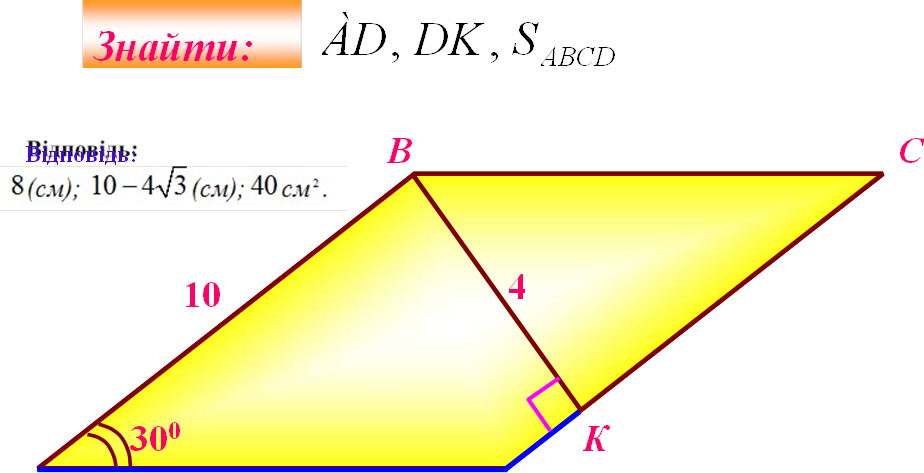
А D
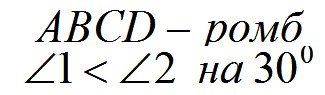
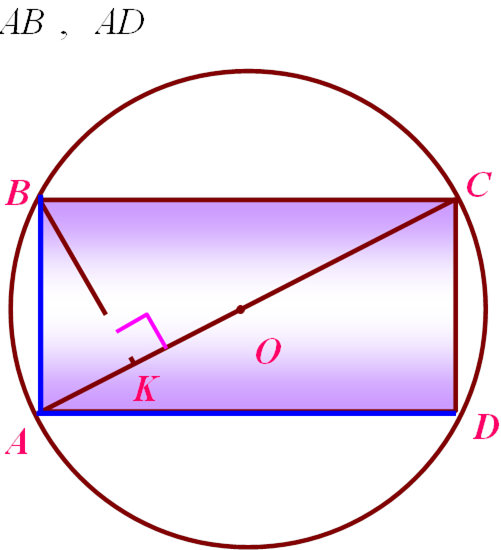
|
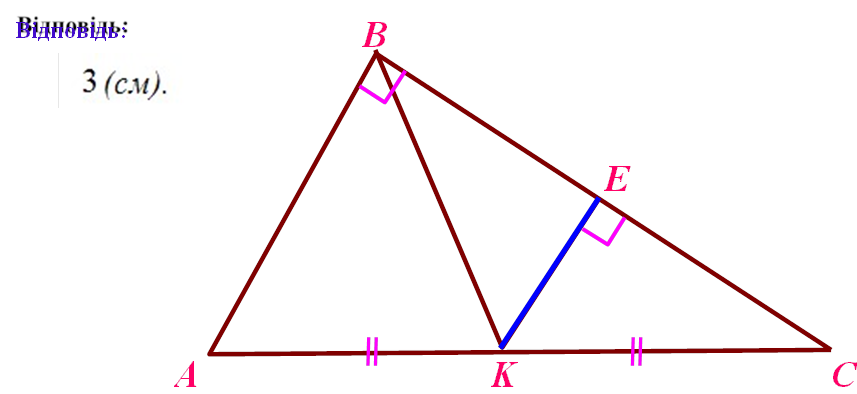
Знайти: |
ÊÅ
|
|
|
C А
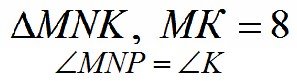
|
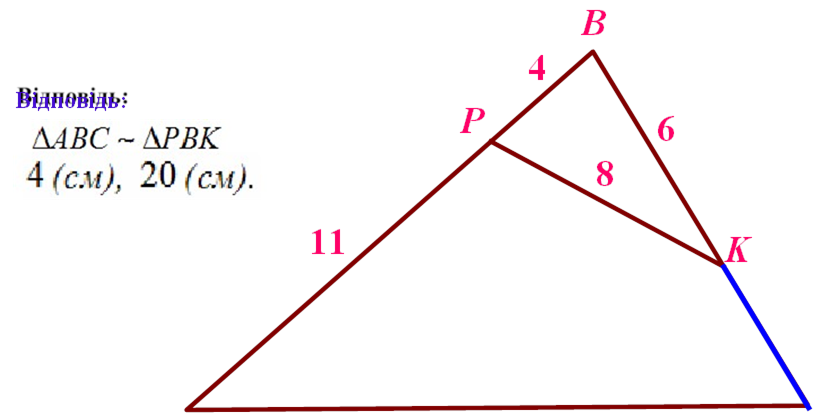
Найти: |
ÐÊ
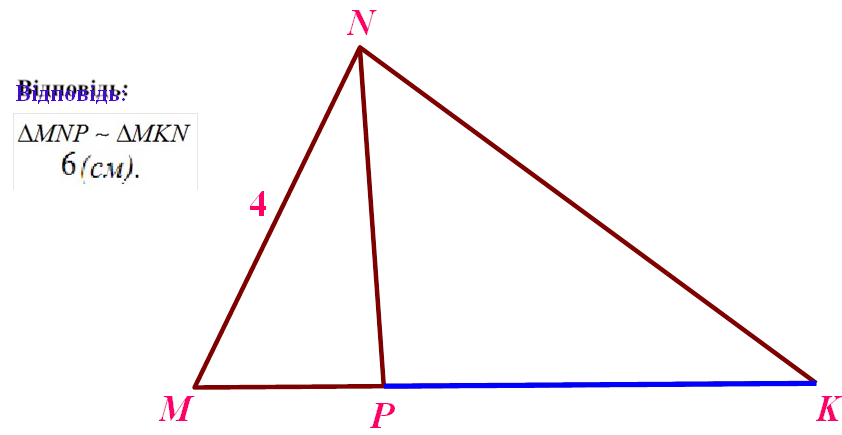
|
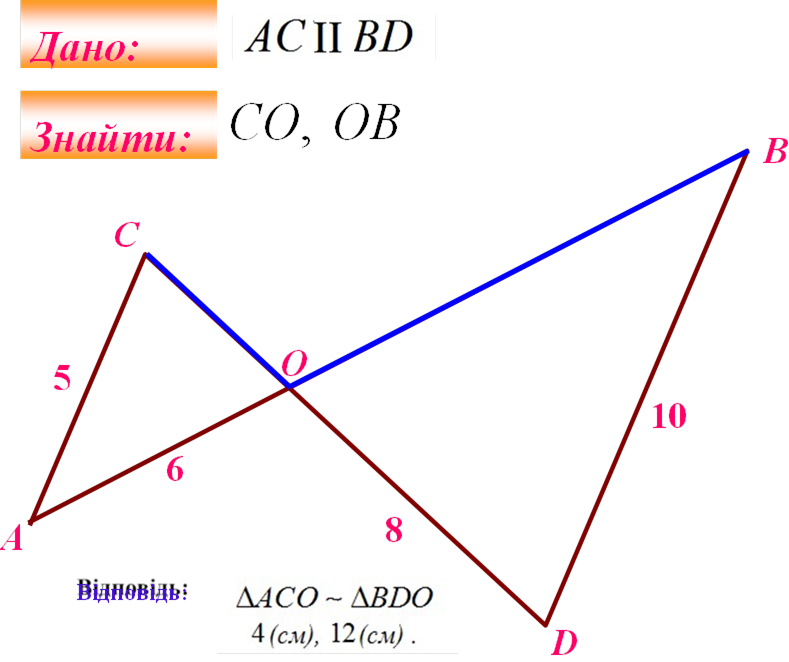
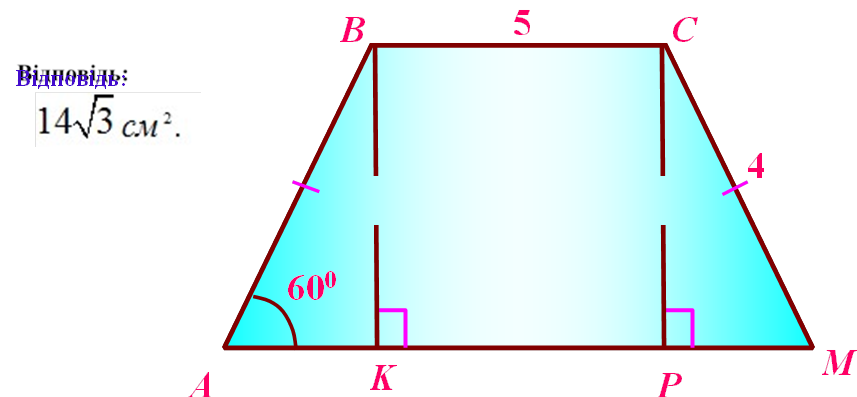
Знайти: |
SAÂCÌ
|
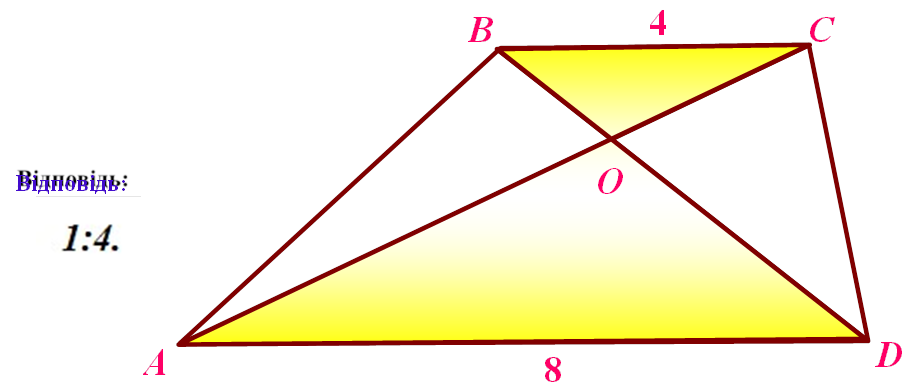
Знайти: |
SBOC
SAOB
|
|
|
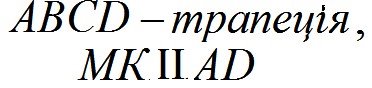
|
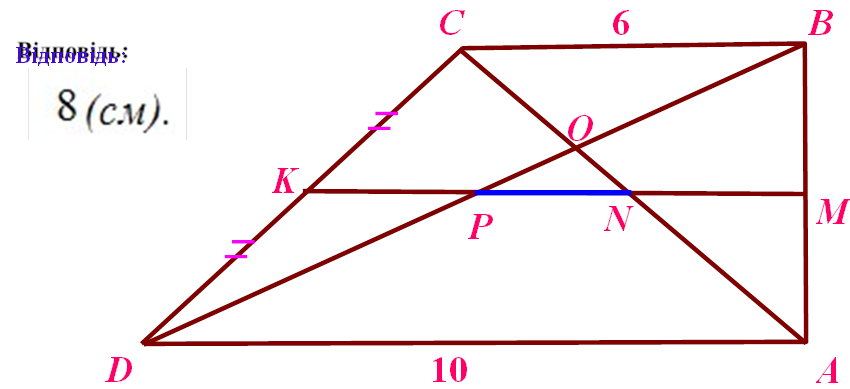
Знайти: |
NP
|
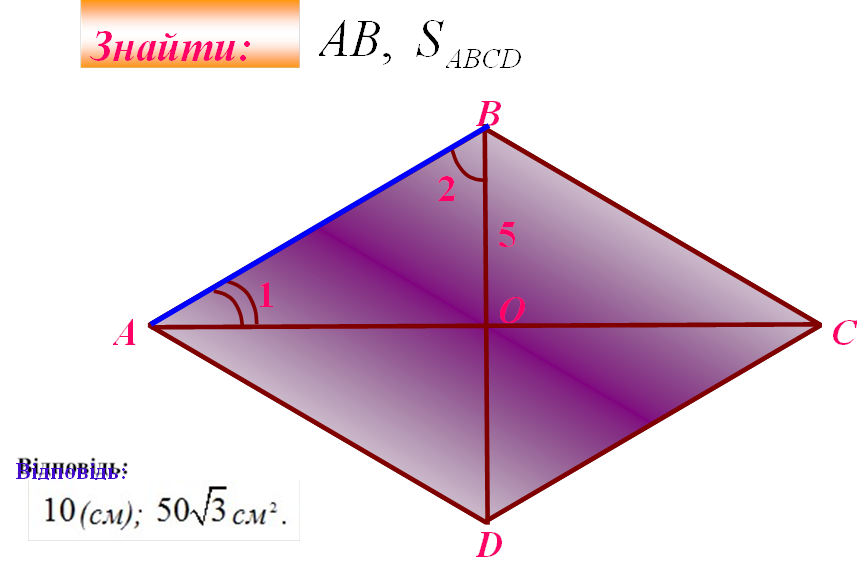
Знайти: |
PAÂÑD, SABCD
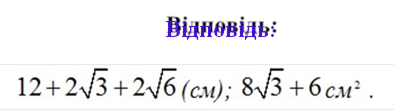
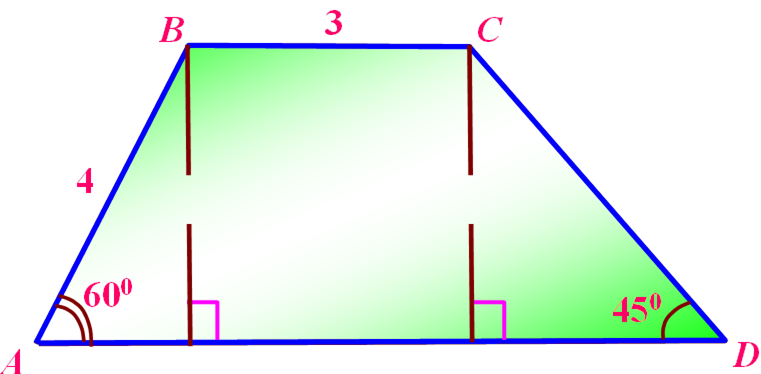
K Р
|
Знайти: |
|
Знайти: |
AOC, PAÂÑ
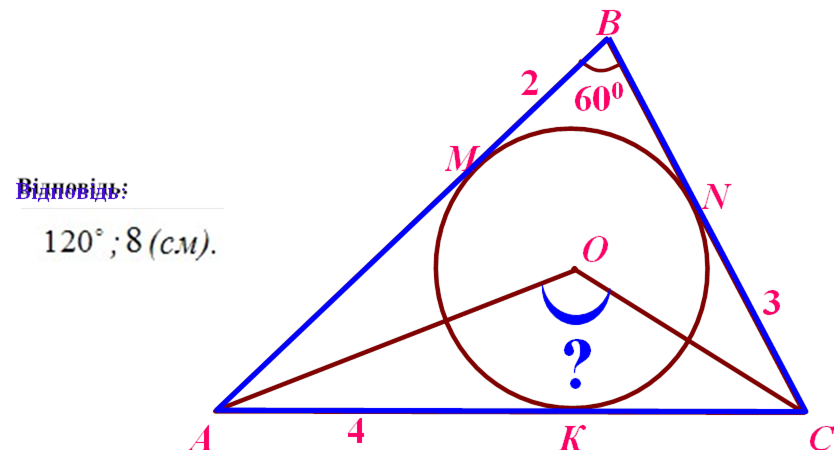
|
Знайти: |
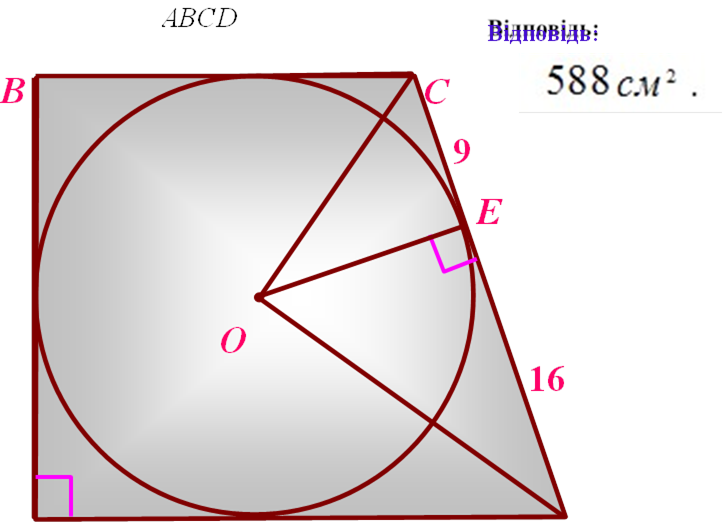 S
S
А D
|
Знайти: |
BòC
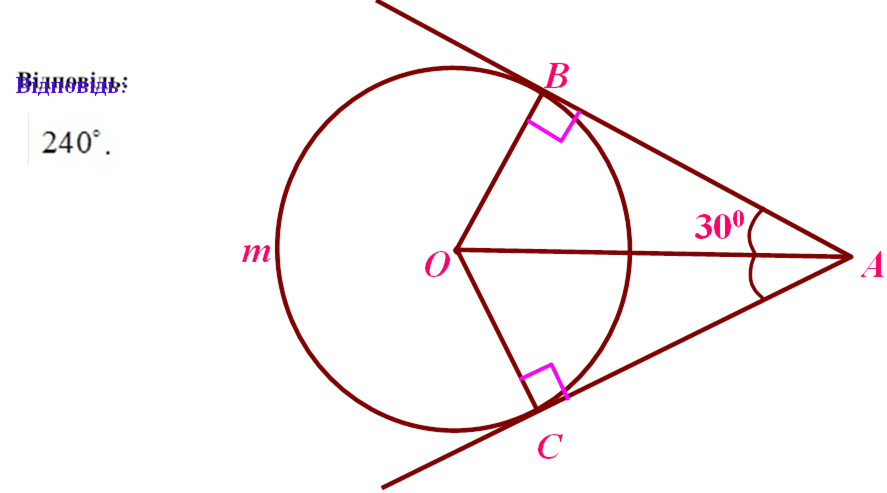
|
|
|
|
Знайти: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
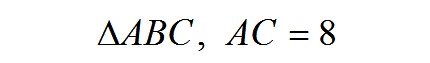
|
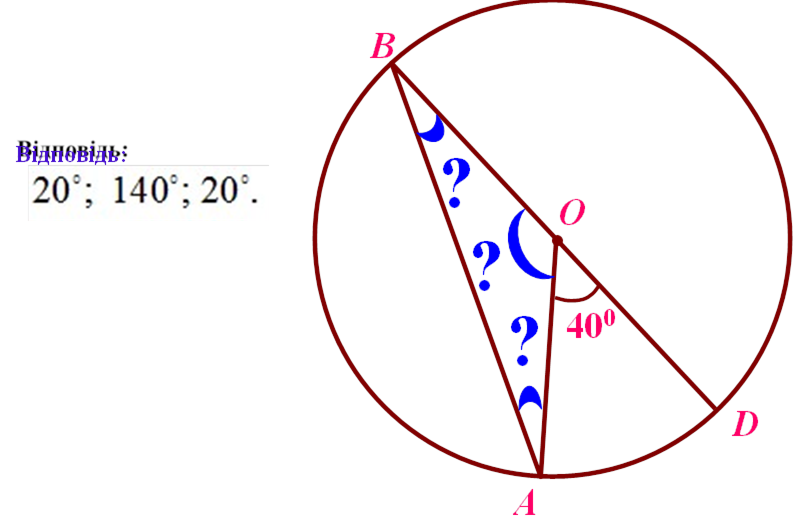
Знайти: |
AÎ , ÂÎ , ÑÎ
|
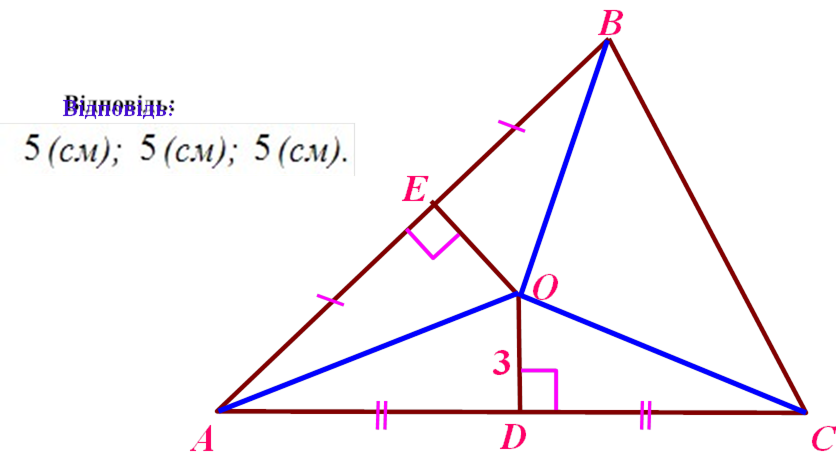
Знайти: |
AÂ
B
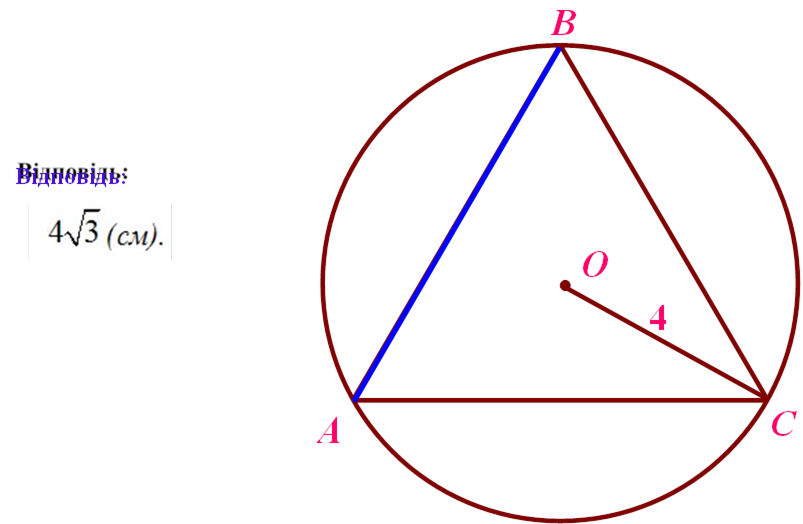
|
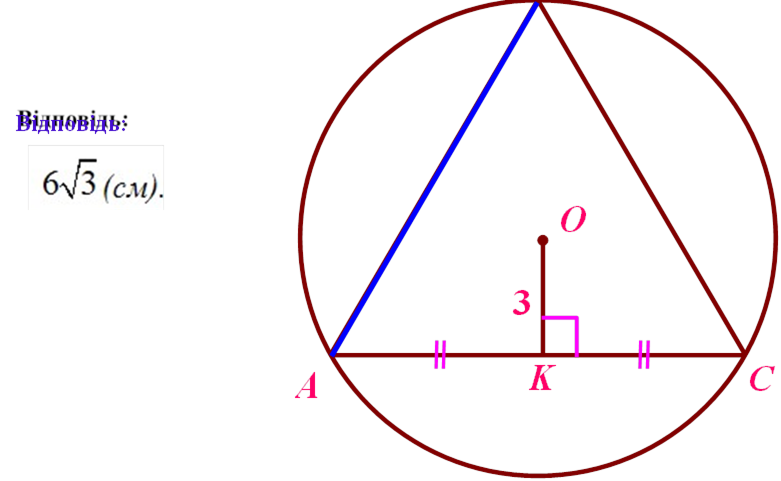
Знайти: |
AÂ
|
|
|
|
|
|
|
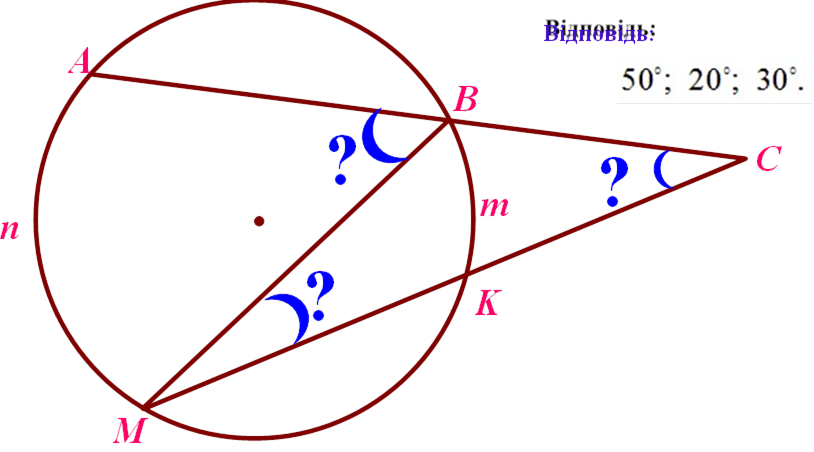
Знайти: |
ÀBM, BMK, ACM
|
|
|
|
|
|
|
Знайти: |
![]()
![]()
![]()
МЕТОД ПРОЄКТІВ
• Відхід від коротких, відокремлених уроків, зосереджених довкола вчителя
• Наголошує на навчальній діяльності, яка є:
– довготерміновою
– у центрі якої знаходиться учень
– пов'язана з проблемами та практикою реального життя і містить захоплюючи питання
• Зміцнює пізнавальні навички вищого рівня та удосконалює стратегії, спрямовані на вирішення проблем
Вчить учнів:
![]() ✓Мислити, застосовувати знання, бути технічно грамотними, здобувати навички ХХІ століття та впевненість у своїх силах
✓Мислити, застосовувати знання, бути технічно грамотними, здобувати навички ХХІ століття та впевненість у своїх силах
 МЕТОД ПРОЄКТІВ
МЕТОД ПРОЄКТІВ
• Заохочує до розвитку:
– Навичок роботи в групі (співпраця)
– Життєво важливих навичок
– Технічних навичок
– Пізнавальних навичок
– Навичок самоуправління
– Позитивного ставлення
• Але
– Не кожен урок повинен базуватися на НМП
– Застосовувати методику навчання методом проектів треба на тих уроках, де це найдоцільніше
КУРІННА ВЕРОНІКА АНАТОЛІЇВНА
МЕТОД ПРОЄКТІВ
Початкова школа: математика
• Мета: Розуміння простих економічних принципів
• Ключове запитання: Хто володіє, чим і чому?
![]() – Проект: Учні виконують роль підприємців, організувавши прості магазини роздрібної торгівлі у своїй школі. Вони розробляють план, який допомагає їм вирішити що продавати, за якою ціною, готують продукцію, здійснюють її маркетинг та обліковують прибутки й збитки.
– Проект: Учні виконують роль підприємців, організувавши прості магазини роздрібної торгівлі у своїй школі. Вони розробляють план, який допомагає їм вирішити що продавати, за якою ціною, готують продукцію, здійснюють її маркетинг та обліковують прибутки й збитки.
КУРІННА ВЕРОНІКА АНАТОЛІЇВНА
МЕТОД ПРОЄКТІВ
Середні класи: математика
• Мета: дізнатися, як математика застосовується у реальному житті
• Ключове запитання: Як я можу отримати те, що бажаю?
![]() – Проект: Учні виконують ролі працюючих дорослих та обирають свою професію, отримують зарплату, шукають будинок, вираховують кредит на придбання житла, складають власний бюджет, учні проектують свій будинок у масштабі, ведуть чекову книжку та облаштовують своє житло. Якщо дозволяє час, можна завершити проекти окремих будинків, спроектованих в масштабі, для забудови своєї місцевості.
– Проект: Учні виконують ролі працюючих дорослих та обирають свою професію, отримують зарплату, шукають будинок, вираховують кредит на придбання житла, складають власний бюджет, учні проектують свій будинок у масштабі, ведуть чекову книжку та облаштовують своє житло. Якщо дозволяє час, можна завершити проекти окремих будинків, спроектованих в масштабі, для забудови своєї місцевості.
МЕТОД ПРОЄКТІВ
Старші класи: Математика
• Мета: Зрозуміти, як працює фондовий ринок та як він впливає на його учасників
• Ключове запитання: Як мені потрібно вкладати гроші?
![]() – Проект: учні засновують компанії, стають інвесторами та брокерами, складають інвестиційні плани та відслідковують їх протягом року.
– Проект: учні засновують компанії, стають інвесторами та брокерами, складають інвестиційні плани та відслідковують їх протягом року.
КУРІННА ВЕРОНІКА АНАТОЛІЇВНА
![]()
STEM - підхід під час вивчення теми
«Коло. Круг»
Наскрізні лінії та предметні
компетентності
![]() Спілкування державною мовою: грамотно висловлюватися рідною мовою; доречно та коректно вживати в мовленні математичну термінологію, чітко, лаконічно та зрозуміло формулювати думку, аргументувати, доводити правильність тверджень Спілкування іноземними мовами: спілкуватися іноземною мовою використанням математичних понять і найуживаніших термінів;
Спілкування державною мовою: грамотно висловлюватися рідною мовою; доречно та коректно вживати в мовленні математичну термінологію, чітко, лаконічно та зрозуміло формулювати думку, аргументувати, доводити правильність тверджень Спілкування іноземними мовами: спілкуватися іноземною мовою використанням математичних понять і найуживаніших термінів;
Соціальна і громадянська компетентності оцінювати аргументи та змінювати думку на основі доказів; аргументувати та відстоювати свою позицію; ухвалювати аргументовані рішення в життєвих ситуаціях; співпрацювати в команді, виділяти та виконувати власну роль в командній
роботі
ДОСЛІДНИЦЬКА ДІЯЛЬНІТЬ УЧНІВ
Практична робота учнів
1. Обміряйте стрічкою по колу довжину отвору склянки.
2. Знайдіть діаметр кола склянки за допомогою лінійки.
3. Обчисліть відношення С/d
4. Повторіть вимірювання інших посудин. Дані запишіть у таблицю.
5. Зробіть висновок.
3.141592653589793238462643383279502884197169399375058209749445923078164062862089986280
3482534211706798214808651328230664709384460955058223172535940812848111745028410270193
8521105559644622948954930381964428810975665933446128475648233786783165271201909145648
5669234603486104543266482133936072602491412737245870066063155881748815209209628292540
9171536436789259036001133053054882046652138414695194151160943305727036575959195309218
![]() 6117381932611793105118548074462379962749567351885752724891227938183011949129833673362 4406566430860213949463952247371907021798609437027705392171762931767523846748184676694 0513200056812714526356082778577134275778960917363717872146844090122495343014654958537 10507922796892589235 Дослідницька робота учнів
6117381932611793105118548074462379962749567351885752724891227938183011949129833673362 4406566430860213949463952247371907021798609437027705392171762931767523846748184676694 0513200056812714526356082778577134275778960917363717872146844090122495343014654958537 10507922796892589235 Дослідницька робота учнів
1. Встановити, яка цифра зустрічається найчастіше серед десяткових знаків числа π.
2. Висновок: різні цифри у десятковому представленні числа π зустрічаються однаково часто (тобто π є нормальним числом), проте це не доведено.
3. Відшукайте номера телефонів мобільного зв'язку, що діють на
Україні.
ДОСЛІДНИЦЬКА ДІЯЛЬНІТЬ УЧНІВ
Цікаве історичне спостереження
Перший мільйон знаків числа π після коми становить:
- 99959 чисел "0"; - 99758 чисел "1";
- 100026 чисел "2"; - 100229 чисел "3";
- 100230 чисел "4"; - 100359 чисел "5"; - 99548 чисел "6"; - 99800 чисел "7"; - 99985 чисел "8"; - 100106 чисел "9".
Вправа «Візуалізація числа π»
![]() Зафарбуйте число 0 вишневим кольором, число 1 оранжевим кольором, число 2 жовтим кольором, число 3 салатовим кольором, число 4 зеленим кольором, число 5 блакитним кольором, число 6 синім кольором, число 7 рожевим кольором, число 8 фіолетовим кольором, число 9 коричневим
Зафарбуйте число 0 вишневим кольором, число 1 оранжевим кольором, число 2 жовтим кольором, число 3 салатовим кольором, число 4 зеленим кольором, число 5 блакитним кольором, число 6 синім кольором, число 7 рожевим кольором, число 8 фіолетовим кольором, число 9 коричневим
кольором.
 Інтеграція курсів математики та історії у 6 класі
Інтеграція курсів математики та історії у 6 класі
Задачі стародавнього Єгипту
Завдання з папірусу Ахмеса
Розділити 7 хлібин між 8 людьми. Якщо різати кожен хліб на 8 частин, доведеться провести 49 розрізів. По-єгипетські ця задача вирішувалася так: дріб 7/8 записували у вигляді часток
Отже, кожній людині треба дати півхліба, чверть хліба і восьмушку хліба; тому чотири хлібини розрізали навпіл, дві хлібини – на 4 частини і один хліб – на 8 частин, після чого кожному давали його частину.
• Відео
• Математика у стародавньому Єгипті https://www.youtube.com/watch?v=ixiYWI a3oro
• Математика Древнього Єгипту
https://www.youtube.com/watch?v=1mNAU915F8
• Як виконували множення стародавні єгиптяни
https://www.youtube.com/watch?v=nICHS BErVRI https://www.youtube.com/watch?v=V-
• Освіта і наука в Давній Греції (укр.) https://www.youtube.com/watch?v=_7QAE
HKKD-k
• З історії математики
https://www.youtube.com/watch?v=9xX33 3dcVME
• Розвиток Давньогрецької науки https://www.youtube.com/watch?v=KLZ5r
2mjr7w
ІНФОРМАЦІЙНІ ТЕХНОЛОГІЇ
![]() Використання мультимедійних технологій дає можливість досягнення наступних педагогічних цілей:
Використання мультимедійних технологій дає можливість досягнення наступних педагогічних цілей:
• Підтримка групових та індивідуальних форм вивчення математики в умовах класно – урочної системи організації навчального процесу;
• Створення комфортних умов комп’ютерної підтримки традиційних і новаторських технологій навчання математики;
• Підвищення пізнавального інтересу учнів до вивчення математики;
• Забезпечення диференційованого підходу до вивчення математики;
• Формування навичок розв’язування задач практичного та дослідницького характеру;
• Структуризація змісту навчання математики та активізації опорних знань.
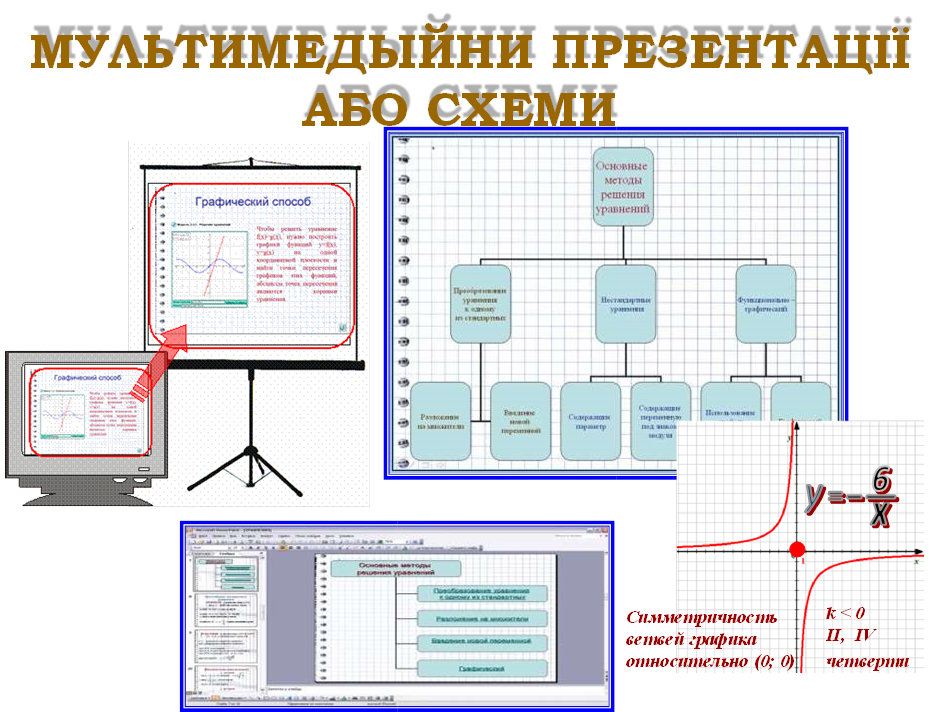
ПРОГРАМА Power Point
Таким чином, використання презентацій на уроках математики:
1. дозволяє враховувати індивідуальні особливості учнів
(оскільки з’являється більше часу на пояснення, вдосконалення вмінь та навичок)
2. ![]() розвиває творчі здібності учнів (учні можуть самі складати презентації,розвиваючи при цьому естетичний смак при оформленні, а також вміння працювати в групах)
розвиває творчі здібності учнів (учні можуть самі складати презентації,розвиваючи при цьому естетичний смак при оформленні, а також вміння працювати в групах)
3. виховує інтерес до предмету (при цікавому і яскравому оформленні навіть дуже важкої теорії)
4. забезпечує якісне засвоєння матеріалу
![]()
ПРОГРАМНОГО ПАКЕТУ GRAN2
Педагогічний програмний засіб "GRAN1" Засіб надає можливість зробити графічний аналіз функцій Педагогічний програмний засіб GRAN-2D Програма призначена для графічного аналізу систем геометричних об'єктів на площині Педагогічний програмний засіб
![]() GRAN-3D ППЗ дозволяє створювати та оперувати моделями геометричних об'єктів поданих нижче типів: точка, відрізок, ламана, площина, многогранник, поверхня обертання та довільна поверхня, при цьому можливе задання
GRAN-3D ППЗ дозволяє створювати та оперувати моделями геометричних об'єктів поданих нижче типів: точка, відрізок, ламана, площина, многогранник, поверхня обертання та довільна поверхня, при цьому можливе задання
об'єктів у різний спосіб
ПРОГРАМНОГО ПАКЕТУ GRAN
![]() Моделююча програма дозволяє будувати геометричні моделі досліджуваних об’єктів, маніпулювати ними (тобто інтерактивно змінювати їх параметри), спостерігати за динамікою змін параметрів цих моделей Моделюючі програми Пакет динамічної геометрії DG “Geometry” У 2000 році було розроблено пакет динамічної геометрії DG “Geometry” (науковий керівник к.ф.м.н. Раков С.А., програміст Осенков К.О., Харківський державний педагогічний університет ім.
Моделююча програма дозволяє будувати геометричні моделі досліджуваних об’єктів, маніпулювати ними (тобто інтерактивно змінювати їх параметри), спостерігати за динамікою змін параметрів цих моделей Моделюючі програми Пакет динамічної геометрії DG “Geometry” У 2000 році було розроблено пакет динамічної геометрії DG “Geometry” (науковий керівник к.ф.м.н. Раков С.А., програміст Осенков К.О., Харківський державний педагогічний університет ім.
Г.С. Сковороди)
Моделюючі програми Gran-
1, Gran-2D, Gran-3D
Пакети відповідають світовому рівню,
досягнутому пакетами динамічної геометрії Автори (c): проф. Жалдак М.І., доц. Горошко Ю.В.
ПРОГРАМНОГО ПАКЕТУ GRAN1
ПРОГРАМНОГО ПАКЕТУ GRAN1
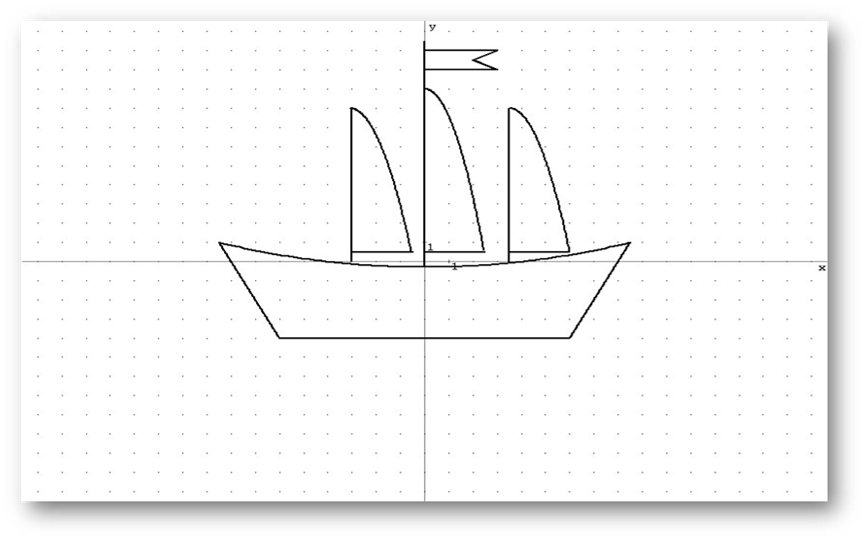
ВИКОРИСТАННЯ ПРИКЛАДНОГО ПРОГРАМНОГО ПАКЕТУ SMath Stidio
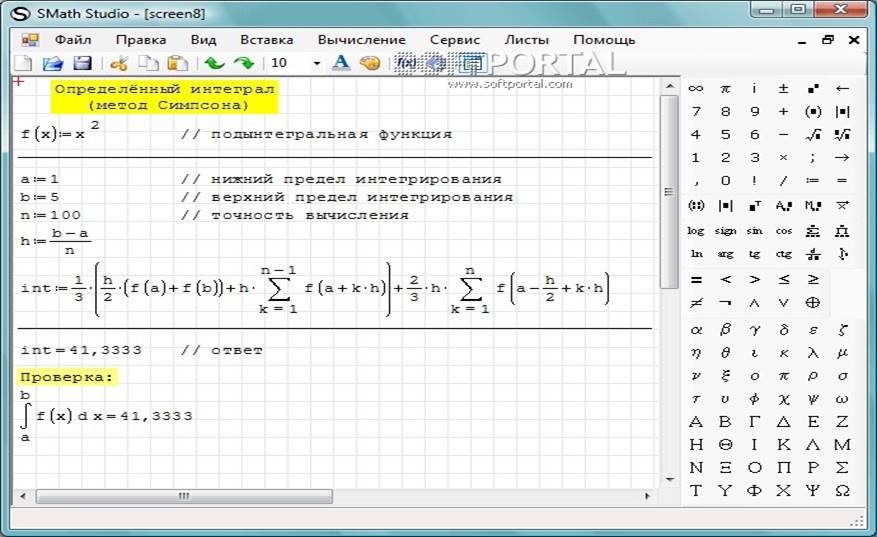
![]()
![]()
![]()
![]() РОБОТА З ЕЛЕКТРОННИМИ
РОБОТА З ЕЛЕКТРОННИМИ
ПІДРУЧНИКАМИ
Підручник Геометрія 9 клас - О. С. Істер
Шановні дев’ятикласники та дев’ятикласниці!
Розділ 1 МЕТОД КООРДИНАТ НА ПЛОЩИНІ
§2. СИНУС, КОСИНУС, ТАНГЕНС КУТІВ ВІД 0 ДО 180. ТРИГОНОМЕТРИЧНІ ТОТОЖНОСТІ
§3. КООРДИНАТИ СЕРЕДИНИ ВІДРІЗКА. ВІДСТАНЬ МІЖ ДВОМА ТОЧКАМИ ІЗ ЗАДАНИМИ КООРДИНАТАМИ §4. РІВНЯННЯ КОЛА
Вправи для повторення розділу 1
![]() Розділ 2 ВЕКТОРИ НА ПЛОЩИНІ
Розділ 2 ВЕКТОРИ НА ПЛОЩИНІ
§6. ВЕКТОР. МОДУЛЬ І НАПРЯМ ВЕКТОРА. КОЛІНЕАРНІ ВЕКТОРИ. РІВНІСТЬ ВЕКТОРІВ
§8. ДОДАВАННЯ І ВІДНІМАННЯ ВЕКТОРІВ
§10. СКАЛЯРНИЙ ДОБУТОК ВЕКТОРІВ Домашня самостійна робота № 2
Вправи для повторення розділу 2
Найвеличніший арифметик своєї епохи
Розділ 3 РОЗВ'ЯЗУВАННЯ ТРИКУТНИКІВ
§13. РОЗВ'ЯЗУВАННЯ ТРИКУТНИКІВ. ПРИКЛАДНІ ЗАДАЧІ
§14. ФОРМУЛИ ДЛЯ ЗНАХОДЖЕННЯ ПЛОЩІ ТРИКУТНИКА
Вправи для повторення розділу З
Розділ 4 ПРАВИЛЬНІ МНОГОКУТНИКИ
§15. ПРАВИЛЬНІ МНОГОКУТНИКИ. ФОРМУЛИ РАДІУСІВ ВПИСАНИХ І ОПИСАНИХ
§16. ДОВЖИНА КОЛА. ДОВЖИНА ДУГИ КОЛА
§17. ПЛОЩА КРУГА ТА ЙОГО ЧАСТИН
![]()
ВИКОРИСТАННЯ ІНТЕРАКТИВНИХ
ФОРМ НАВЧАННЯ ПІД ЧАС УРОКІВ МАТЕМАТИКИ
«Те, що я чую, я забуваю. Те, що я бачу і чую,
я трохи пам'ятаю. Те, що я бачу, обговорюю, я починаю розуміти. Коли я чую, бачу, обговорюю й роблю, я набуваю знань і навичок. Коли я передаю знання іншим, я стаю майстром»
Конфуцій
![]() Організація інтерактивного навчання передбачає моделювання життєвих ситуацій, використання рольових ігор, спільне вирішення проблеми на основі аналізу обставин та відповідної ситуації.
Організація інтерактивного навчання передбачає моделювання життєвих ситуацій, використання рольових ігор, спільне вирішення проблеми на основі аналізу обставин та відповідної ситуації.
![]()
ПРАВИЛА ДЛЯ УЧНІВ ПІД ЧАС
![]() ВИКОРИСТАННЯ ІНТЕРАКТИВНИХ МЕТОДІВ
ВИКОРИСТАННЯ ІНТЕРАКТИВНИХ МЕТОДІВ
Не бійся
Тільки Кожна думка висловитися!
обґрунтовані важлива! Ми всі –
докази! партнери!
Обговорюємо Обдумав, Говори чітко, сказане, а не сформулював, ясно,
людину! висловив! красиво!
Вмій
Вислухав, Важлива
погодитися і
висловився, кожна роль!
не вислухав! погодитися!
![]()
![]() УЧАСТЬ У КОНКУРСАХ
УЧАСТЬ У КОНКУРСАХ
Навчальний Конкурс Учні (ПІБ), клас Рівень, рік результат
2017 – 2018 Мiжнародний математичний Грігорян Сертифікат
Віталій
конкурс «Кенгуру» Жерздєв відмінний
Ілля
Огар
![]() Єва
Єва
Станкевич Софія
2018 – 2019Грігорян Сертифікат
Віталій відмінний
Жерздєв
Ілля
Огар
Єва
Станкевич Софія
2019 – 2020Грігорян Сертифікат
Віталій відмінний
Жерздєв
Ілля
Огар
Єва
Станкевич Софія
Сертифікат
2020-2021 Мiжнародний математичний 15 учныв відмінний конкурс «Кенгуру»
![]()
ВИСНОВКИ
Використання інноваційних технологій на уроках математики дає можливість доповнити
уроки різноманітною інформацією, а різні види
діяльності заохочують моїх учнів до роботи. Діти свідомо осмислюють положення (ситуацію):
![]() «відсидіти не вдається». Кожен учень зацікавлений у правильності своєї думки. Продуктивність уроків підвищується.
«відсидіти не вдається». Кожен учень зацікавлений у правильності своєї думки. Продуктивність уроків підвищується.
Те, що подобається, учень робить із задоволенням і натхненням, а значить – навчається
КУРІННА ВЕРОНІКА АНАТОЛІЇВНА


про публікацію авторської розробки
Додати розробку