План заняття № _____

 

Вид заняття  - лекція

Тема:  Теорія ймовірностей.

Мета заняття : познайомити учнів з операціями над подіями: подія, протилежна даній; сума подій; добуток подій. Вчити виражати складену подію через суму і добуток про­стих подій, вчити обчислювати ймовірності випадкових подій використовуючи формули комбінаторики та класич­не означення ймовірності. Розвивати комунікативні здібності, увагу, уміння лаконічно й математично грамотно висловлювати свою думку. Виховувати працелюбність, інтерес до предмету.

Методи : словесні, інтерактивний, особистісно-орієнтований, практичні. Матеріально-технічне забезпечення та дидактичні засоби, ТЗН: таблиця, роздатковий матеріал, геометричні приладдя

 

 

 Структура заняття                                    відведений час

1. Організаційна частина:  контроль відвідування                                     3 хв

2. Актуалізація опорних знань                                                                     25 хв

• Контроль виконання домашніх вправ
• Розв’язування задач усно.

• Скількома способами можна вибрати трьох чергових з класу, в якому 20 учнів? (Відповідь: =1140)
• В одній коробці лежать 5 олівців, в другій – 8 ручок. Скількома способами можна вибрати: а) або 1 олівець, або 1 ручку; б) один олівець і одну ручку. ( Відповідь: а) 13; б) 40)
• Скільки існує способів розмістити 5 гостей за столом, за яким 5 столових приборів? (Відповідь: 120)
• Скільки можна провести різних площин через 8 точок простору, якщо ніякі чотири не лежать в одній площині. (Відповідь:56)

• Фронтальне опитування теоретичного блоку за допомогою технології «Незакінчене речення».

3. Повідомлення теми, формування мети та основних                              2 хв

завдань

4. Мотивація навчальної діяльності                                                               5 хв

5. Вивчення матеріалу за планом:                                                                   30 хв

1. Операції на подіями.

2. Використання формул комбінаторики для  обчислен­ня ймовірностей подій.

- 1 -

Обчислювати ймовірність подій, будуючи кожний раз мно­жину елементарних подій і підраховуючи число подій, що спри­яють цій події, інколи важко. Тому для обчислення ймовірнос­тей користуються правилами, які дозволяють за відомими ймо­вірностями одних подій обчислювати ймовірності інших подій, які утворюються з них за допомогою деяких операцій.

На сьогоднішньому занятті ми познайомимося з операціями над подіями.

Сумою подій А і В називається подія С, що полягає в здійсненні під час одиничного випробування або події А, або події В, або обох подій одночасно.

Суму двох подій позначають так:

С = А + В або С = A U В.

Графічно суму подій можна зобразити як об'єднання множин (рис. 128). Суму подій А і В, як і суму множин, називають об'єднанням. На рис. 128, а зображено об'єднання (суму) сумісних подій А та В, на рис. 128, б зображено суму двох несумісних подій А і В, яка полягає в здійсненні або події А, або події В (одночасна поява подій А і В виключена).

  

Рис. 128

Приклад. Якщо подія А — «влучення в ціль з першого пост­рілу», подія В — «влучення в ціль з другого пострілу», то подія С = А + В — «влучення в ціль».

Виконання вправ

1. Проводиться випробування кидання двох монет. Розглядають­ся такі події:

А — «випав герб на першій монеті»;

В — «випала цифра на першій монеті»;

С — «випав герб на другій монеті»;

D — «випала цифра на другій монеті».

Що означають події:

а)А+С;     б) В + D;    в)A+D;     г) В + С.

Відповіді: а) випав хоча б один герб; б) випала хоча б одна циф­ра; в) випав герб на першій монеті або випала цифра на другій монеті; г) випала цифра на першій монеті або випав герб на другій монеті.

Подія називається протилежною до події А, якщо вона відбу­вається тоді і тільки тоді, коли подія А не відбувається. Чи­тається — «не А».

Приклад 1. Якщо подія А — «попадання в ціль при пострілі», то подія — «промах при пострілі».

Приклад 2. Якщо подія А — «взято стан­дартну деталь» при випробуванні — на­вмання взято деталь із ящика, то «взя­то нестандарту деталь».

Виконання вправ

1. Вкажіть події, протилежні до подій:

А — «випали два герба при киданні двох монет»;

В — «вийнято білу кульку при витягуванні однієї кульки з урни, в якій 2 білих, 3 чорних і 4 червоних кульки»;

С — «три попадання при трьох пострілах»;

D — «хоча б одне попадання при п'яти пострілах»;

Е — «не більше двох попадань при п'яти пострілах»;

F — «виграш одного гравця при грі в шахи».

Відповіді: — «випала хоча б одна цифра»;

— «вийнято чорну або червону кульку»;

               — «хоча б один промах»;

               — «всі п'ять промахів»;

— «більше двох попадань»;

— «виграш другого гравця або нічия».

2. По мішені проводиться два постріли. Розглядаються події:

А — «попадання при першому пострілі»;

В — «попадання при другому пострілі».

Що означають події:

а) А + ;     б) + В;     в) + ;     г) .

Відповіді: а) попадання при першому пострілі або промах при другому пострілі; б) промах при першому пострілі або попадан­ня при другому пострілі; в) хоча б один промах; г) промах при двох пострілах.

 

Добутком подій А і В називається подія С, що полягає в здійс­ненні обох подій А і В під час одиничного випробування.

Добуток двох подій А і В позначають так: С = А · В або С = АВ, або С = АВ.

Графічно добуток двох подій, як і двох множин, зображається так, як на рисунку 130:

Приклад. Якщо подія А — «перший стрілець влучив у ціль», подія В — «другий стрілець влучив у ціль», тоді подія С =А·В — «в ціль влучили обидва учасники».

Виконання вправ

1. Випробування полягає в тому, що кидається дві монети. Роз­глядаються події:

А — «випав герб на першій монеті»;

В — «випала цифра на першій монеті»;

С — «випав герб на другій монеті»;

D — «випала цифра на другій монеті»;

Е — «випав хоча б один герб»;

F — «випала хоча б одна цифра»;

G — «випали один герб і одна цифра»;

Η — «не випав ні один герб»;

Κ — «випало два герби».  

Визначте, яким подіям із даного списку рівносильні такі події:

а) А·С;      б) E·F;      в)G·E;       г) В · D.

Відповіді: а) А · С = К; б) Е · F = G; в) G · Е = G; г) В · D = Н.

У теорії ймовірності розрізняють прості і складені події.

Наприклад, під час кидання двох монет подія А — «на першій монеті випав герб» є простою.

Подія називається складеною, якщо поява її залежить від появи інших, простих подій.

Наприклад, під час кидання двох монет подія А — «випав хоча б один герб» — складена, бо вона складається з таких подій:

A₁ — «випав герб тільки на першій монеті»;

А₂ — «випав герб тільки на другій монеті»;

А₃ — «випав герб на обох монетах»,

тобто А = А₁ + A₂ + А₃.

Нехай А, В, С — деякі випадкові події. Знайдіть вирази для подій, які полягають у тому, що:

а) настала тільки подія А;

б) настали події А і В, але подія С не настала;

в) настала принаймні одна з цих подій;

г) не настала жодна з цих подій;

д) настали всі три події;

є) настало не більше двох подій.

Відповіді: а) А··;   б) А·В·;   в) А+В+С;  г) ··;  д)А·В·С;  є) ··.

-2-

Безпосередній підрахунок ймовірностей подій значно спро­щується, якщо використовувати формули комбінаторики. Пра­вильність розв'язання задачі залежить від уміння визначити вид сполуки, що утворюються сукупністю подій, про які йдеться мова в умові задачі. Згадаємо алгоритм визначення виду сполуки (таб­лиця 15). Розглянемо приклади розв'язування задач.

Задача 1. В урні лежать 20 кульок, з яких 12 білих, решта — чорні. З урни навмання виймають дві кульки. Яка ймовірність того, що вони білі?

Розв'язання

Загальна кількість елементарних подій випробування (вий­нято дві кульки) дорівнює числу способів, якими можна вийня­ти 2 кульки із 20, тобто числу комбінацій із 20 елементів по 2 (n = ). Підрахуємо кількість елементарних подій, які сприя­ють події «вийнято дві білих кульки». Ця кількість дорівнює числу способів, якими можна вийняти 2 кульки із 12 білих, тобто числу комбінацій із 12 елементів по 2 (т = ).

Отже, якщо подія А — «вийнято дві білі кульки», то

Відповідь: ·

Задача 2. В урні лежать 20 кульок, з яких 12 білих, решта — чорні. З урни навмання виймають три кульки. Яка ймовірність того, що серед вибраних дві кульки білі?

Розв'язання

Загальна кількість елементарних подій випробування (вий­нято три кульки) дорівнює n = .

Підрахуємо кількість елементарних подій, які сприяють події «серед трьох вибраних кульок дві білі». Дві білі кульки із 12 білих кульок можна вибрати способами, а одну чорну куль­ку можна вибрати 8 способами, тоді події «серед трьох вибраних кульок дві білі» сприяють т = ·8 елементарних подій.

Отже, якщо подія А — «серед трьох вибраних кульок дві білі», то

Відповідь: ·

Задача 3. В урні лежать 15 червоних, 9 синіх і 6 зелених кульок однакових на дотик. Навмання виймають 6 кульок. Яка ймо­вірність того, що вийнято: 1 зелену, 2 синіх і 3 червоних ку­льки?

Розв'язання

В цій задачі випробування полягає в тому, що із урни вийма­ють 6 кульок. Вийняти шість кульок із 15 + 9 + 6 = 30 кульок можна n = способами. Нас цікавить ймовірність події А — «вийнято 1 зелену, 2 синіх і 3 червоних кульки». Одну зелену кульку можна вийняти способами, 2 синіх кульки можна вийняти способами, 3 червоних кульки можна вийняти способами. Отже, події А сприяють т = ·· елементарних подій. Тоді

Відповідь: ·

 

6. Узагальнення матеріалу:                                                                           10хв

 Виконання вправ              

1. В урні знаходиться 12 кульок: п'ять білих і сім чорних. На­вмання виймають три кульки. Яка ймовірність того, що се­ред вийнятих кульок:

а) всі три чорні;    б) дві чорні і одна біла; 

в) одна чорна і дві білі;   г) всі три білі?

 Відповіді: а) 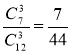; б) ; в) ; г) .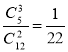

2. Набираючи номер телефону, абонент забув дві останні цифри і, пам'ятаючи лише, що ці цифри різні, набрав їх навмання. Яка ймовірність того, що номер набрано правильно?

Відповідь: .

3. При грі в «Спортлото» на спеціальній картці відмічається 6 номерів із 49. Під час тиражу визначаються 6 виграшних номерів. Яка ймовірність вгадати рівно 3 виграшних номера?

Відповідь: .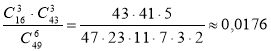

4. У ліфт 9-поверхового будинку на першому поверсі зайшли 6 чоловік. Знайдіть ймовірність того, що всі вийдуть на різних поверхах, якщо кожний з однаковою ймовірністю може вийти на будь-якому поверсі, починаючи з другого.

Відповідь:  ·

5. З 10 лотерейних білетів два виграшних. Знайдіть ймовірність того, що серед узятих будь-яких п'яти білетів: а) один ви­грашний; б) принаймні один виграшний?  

Відповіді: a) 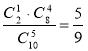;    б) .

6. 9 пасажирів сідають у 3 вагони. Знайдіть ймовірність того, що: а) у кожний вагон сяде по три пасажири; б) в один з ва­гонів сядуть 4, у другий — Зів третій — 2 пасажири.

Відповіді: а) ;    б) .

7. Знайдіть ймовірність того, що дні народження 12 чоловік при­падають на різні місяці року.

Відповідь: .

8. Гральний кубик підкидають двічі. Знайдіть ймовірність того, що:

а) у сумі випаде 6 очок;

б) у сумі випаде 7 очок;

в) за два кидки випаде однакова кількість очок;

г) за два кидки випаде різна кількість очок.

Відповіді: а) ;   б) ;    в) ;    г) .

9. У шаховому турнірі беруть участь 20 чоловік, які жеребкуван­ням розподіляються на дві групи по 10 чоловік. Знайдіть ймо­вірність того, що: 4 найсильніших гравці потраплять по два в різні групи.

Відповідь: .

Самостійна робота (оцінки за роботу будуть оголошені на наступному уроці)

Варіант 1

В скриньці лежать 12 білих і 8 червоних однакових на дотик кульок.

1.  Вийнято навмання одну кульку. Яка ймовірність того, що вона біла?

( Відповідь: ) (3 бали)

2. Вийнято навмання одну кульку. Яка ймовірність того, що вона не біла?

( Відповідь: ) ( 3 бали)

3. Вийнято навмання дві кульки. Яка ймовірність того, що вони білі?

(Відповідь: = ) ( 3 бали)

4. Вийнято навмання дві кульки. Яка ймовірність того, що вони одного кольору? ( Відповідь: = ) ( 3 бали )

Варіант 2

В скриньці лежать 12 білих і 8 червоних однакових на дотик кульок.

1. Вийнято навмання одну кульку. Яка ймовірність того, що вона червона?

( Відповідь: ) (3 бали)

2. Вийнято навмання одну кульку. Яка ймовірність того, що вона не червона?

( Відповідь: ) ( 3 бали)

3. Вийнято навмання дві кульки. Яка ймовірність того, що вони червоні?

(Відповідь: = ) ( 3 бали)

4. Вийнято навмання дві кульки. Яка ймовірність того, що вони різного кольору? ( Відповідь: = 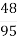) ( 3 бали )

 

 

7. Підведення підсумків:                                                                                 5хв

  Інтерактивна вправа «Незакінчене речення» у поєднання з «Мікрофоном». (викладач формулює незакінчене речення і пропонує студентам висловитися щодо підсумку уроку, закінчуючи його. Кожний наступний студент повинен починати свій виступ із запропонованої формули. Відповідають студенти по черзі за допомогою «мікрофону» (ручка, олівець).

Студенти працюють з відкритими реченнями:

«Сьогодні на занятті ми дізналися про…»

 «На занятті я відкрив для себе…»                                                                                                                     

8. Видача завдання для самостійної роботи студентів:    опрацювати матеріал по підручнику та зробити скрайб-презентацію по ньому