Урок "Лінійні нерівності та системи лінійних нерівностей".
Лінійні нерівності та системи лінійних нерівностей.
Тема: Розв’язання лінійних нерівностей та систем лінійних нерівностей.
Мета: продовжити, на основі компетентністного підходу у навчанні, формування понять нерівності, системи нерівностей, відпрацювати алгоритм розв’язання лінійних нерівностей, систем лінійних нерівностей. Поглибити знання учнів про сферу застосування властивостей нерівностей з однією змінною, розвивати вміння аналізувати, знаходити раціональний спосіб роз’язування лінійних нерівностей та їх систем для набуття сталих певних компетентностей, що можуть реалізовуватися на практиці.
Хід уроку.
І Організаційний момент.
Сьогодні ми працюємо в особливому режимі. Ви всі співробітники банків.
На території «М» сьогодні працюють:
банк «Мрія»
банк «Великі гроші»
банк «Довіра»
Усі банки знаходяться під наглядом Національного Банку.
ІІ Мотивація навчальної діяльності.
У період світової кризи всі ваші банки повинні не тільки зберегти свої капітали, а ще й примножити їх, боротися за кожного клієнта.
Над цим потрібно наполегливо працювати як кожному працівнику банка, так і всьому колективу в цілому.
ІІІ Повідомлення теми і мети уроку.
(дошка)
ІV Актуалізація опорних знань.
Для початку кожному банку необхідно придбати початковий капітал.
Перевірити домашнє завдання, виконавши тестування.
Візьміть тест (додаток)
На чистому аркуші вкажіть своє прізвище і оберіть в кожному завданні номер правильної відповіді, записавши його. Необхідно одержати відповідний кодовий номер.
Тест. Перевірка коду (244323432234)
Обведіть неправильні відповіді і по кількості правильних відповідей, виставте собі оцінку.
V Раунд переговорів щодо продажу акцій частого попиту.
(аналіз основних теоретичних фактів)
Кожний банк ставить по 2 теоретичних запитання своїм сусідам. Правильна відповідь приносить 1 бал.
- Що називається нерівністю?
- Який символ використовується для вислову «не більше»?
- Що означає розв’язати нерівність?
- Що називається розв’язком нерівності?
- Що означає розв’язати систему?
- Що означає розв’язати сукупність?
- Які нерівності називаються рівносильними?
- За допомогою якого символу записується система?
- За допомогою якого символу записується сукупність?
- Коли множина розв’язків нерівності є порожньою?
- Яка з нерівностей є наслідком для другої?
- Яка нерівність називається строгою?
- Формула лінійних нерівностей (задайте).
VI Застосування знань та вмінь.
Секційна робота з окремими банкірами.
Прошу президентів банків відправити у відрядження по одному працівнику.
Розв’язати нерівності.
![]()
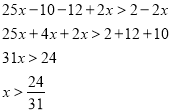
![]()
![]()
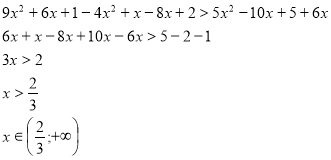
![]()
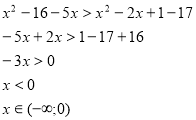
До банківських відділень надійшли запитання від постійних клієнтів, відповіді на які прохання надати у письмовому вигляді.
Відділу кредитів
Знайти всі цілі числа, які є розв’язками неравності ![]()
![]()
![]()
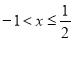
![]()
Відділу роботи з людьми похилого віку
Бабусі просили надати правильну відповідь на нерівності, щоб перевірити домашнє завдання в онуків.
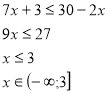
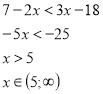
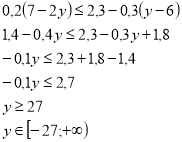
Відділу дружби
Чи можуть бути однакові відповіді для нерівності і системи нерівностей?
![]()
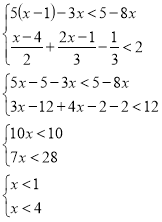
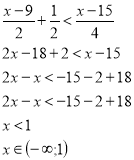
![]()
Недостатньо вміти розв’язувати нерівності, потрібно ще й уміти застосовувати ці вміння для практичних потреб.
Відділу практичних застосувань
Скільки потрібно долити 50% оцтової есенції до 6% оцту, щоб одержати для консервації оцет з концентрацією не менше від 9% і не більше за 10%? (Розрахувати для 1 л розчину)
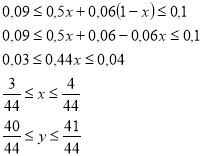
Відділу довіри
(Віриш? Чи не віриш? Що розв’яжеш?)
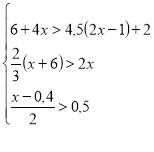
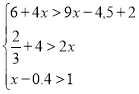
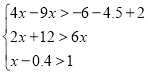
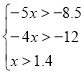
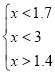
![]()
![]()
Відділу безпеки
Чи були допущені помилки при розв’язуванні нерівностей? У якому місці? (підкресліть, якщо вони є).
Прошу завершити роботи, передати президентам банків.
Переходимо до раунду переговорів щодо обміну досвідом. (обмін роботами, перехресна перевірка).
Додаткові завдання (для бажаючих):
- При яких b рівносильні нерівності:
![]()
![]()
![]()
![]()
- Розв’язати графічно
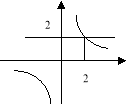
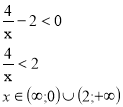
- Розв’яжіть нерівність:
![]()
![]()
-
Які нерівності є наслідками нерівності
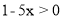
-
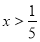 ; 2.
; 2. 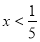 ; 3.
; 3. 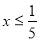 ; 4.
; 4. 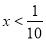 ; 5.
; 5. 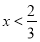 ; 6.
; 6. 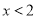
Підсумки уроку.
Додаток
Тест
1) Розв’язати нерівність: 0x ≥ 0
|
1) 0 |
2) (-∞; +∞) |
3) Ø |
4) [ 0; +∞ ) |
2) Розв’язати нерівність: 3x < 0
|
1) (-∞; +∞) |
2) (-∞; 0 ] |
3) (0; +∞) |
4) (-∞; 0) |
3) Запишіть множину розв'язків системи, зображену на малюнку.
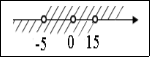
|
1) (-∞; +∞) |
2) (-5; 15 ) |
3) (0; 15) |
4) (-5; 0) U ( 0; 15) |
4) Розв'яжіть систему: ![]()
|
1) (-∞; +∞) |
2) (-∞; 0 ] |
3) [ 0; +∞ ) |
4) Ø |
5) 1) Розв’язати нерівність: (x – 5)2 > 0
|
1) (-∞; +∞) |
2) (-∞; 5) U ( 5; +∞) |
3) ( 5; +∞) |
4) [ 5; +∞) |
6) Назвіть найбільше ціле число на проміжку: (-∞; -6)
|
1) - 5 |
2) - 6 |
3) - 7 |
4) - 8 |
7) Назвіть цілі розв'язки нерівності: - 2 ≤ y < 3
|
1) - 1; 0; 1; 2 |
2) - 2; - 1; 0; 1; 2; 3 |
3) - 1; 0; 1; 2; 3 |
4) - 2; - 1; 0; 1; 2 |
8) При яких х нерівність – х > 0 правильна?
|
1) (-∞; +∞) |
2) Ø |
3) (-∞; 0 ) |
4) ( 0; +∞ ) |
9) Чи правильна нерівність: | х | < 0
|
1) так |
2) ні |
10) Розв’язати нерівність: - 2x > 8
|
1) (-∞; 4) |
2) (-∞; - 4) |
3) ( - 4; +∞) |
4) ( 4; +∞) |
11) Що більше: а чи – а?
|
1) а |
2) - а |
3) відповідь залежить від числа |
12) При яких значеннях m система не має розв'язку?
![]()
|
1) (-∞; 7) |
2) (-∞; 6) |
3) ( 7; +∞) |
4) ( 6; +∞) |


про публікацію авторської розробки
Додати розробку
