Урок "Логарифмічні рівняння"
11 клас.
Тема уроку. Логарифмічні рівняння.
Формування компетентностей:
предметна компетентність:сформувати поняття логарифмічного рівняння; сформувати вміння розв’язувати найпростіші логарифмічні рівняння за означенням логарифма; ознайомити зі способами розв’язання логарифмічних рівнянь шляхом використанням властивостей логарифма й логарифмічної функції та зведенням до алгебраїчних рівнянь шляхом заміни змінних;
спілкування державною мовою: аргументувати, доводити правильність тверджень;
інформаційно –цифрова компетентність: діяти за алгоритмом та складати алгоритми.
Тип уроку: засвоєння нових знань і вмінь.
Обладнання та наочність: презентація.
Хід уроку.
І. Організаційний етап.
ІІ. Перевірка домашнього завдання, повторення матеріалу.
1. Надайте означення логарифма.
2. Пригадайте основну логарифмічну тотожність.
3. Встановіть відповідність між логарифмом та його значенням:
|
Логарифм |
Значення логарифма |
|
|
А. 3 |
|
|
Б. |
|
3) |
В. - 1 |
|
|
Г. 2 |
|
|
Д. - 6 |
ІІІ. Вивчення нового матеріалу.
1). Означення логарифмічного рівняння.
2). Приклади розв’язання логарифмічних рівнянь.
1. Означення . Рівняння називають логарифмічним, якщо його змінні входять лише під знак логарифмів.
Рівняння виду ![]() = b, де a > 0, a ≠ 1, називають найпростішим логарифмічним рівнянням.
= b, де a > 0, a ≠ 1, називають найпростішим логарифмічним рівнянням.
Приклади. ![]() = 3;
= 3; ![]() = - 2;
= - 2; ![]() = - 5;
= - 5; ![]() - 2x ) = 0.
- 2x ) = 0.
Оскільки графіки функцій y = ![]() і y = b перетинаються в одній точці, то найпростіше логарифмічне рівняння
і y = b перетинаються в одній точці, то найпростіше логарифмічне рівняння ![]() = b має єдиний корінь при будь якому значенні b. Цей корінь можна знайти, використовуючи означення логарифма x =
= b має єдиний корінь при будь якому значенні b. Цей корінь можна знайти, використовуючи означення логарифма x = ![]()
![]()
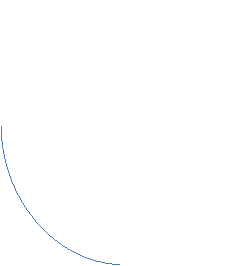
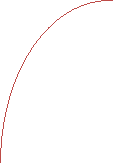 y y =
y y = ![]() , a > 1 y y =
, a > 1 y y = ![]() , a< 1
, a< 1
![]()
![]()
![]()
![]()
![]() b b
b b
y = b y= b
![]()
![]() 0 1
0 1 ![]() x 0
x 0 ![]() 1 x
1 x
1. Найпростіші логарифмічні рівняння ![]() = b
= b
Приклад . Розв’яжіть рівняння 1). ![]() = -1; 2).
= -1; 2). ![]() = 1.Розв’язання . 1). За означенням логарифма
= 1.Розв’язання . 1). За означенням логарифма ![]() = -1 маємо x =
= -1 маємо x = ![]() ; x =
; x = ![]() 2). Так саме
2). Так саме ![]() = 1 будемо мати, що x - 1 =
= 1 будемо мати, що x - 1 = ![]() , х = 3.
, х = 3.
Відповідь. 1) ![]() ; 2) 3.
; 2) 3.
2. Рівняння виду ![]() =
= ![]() .
.
Оскільки функція y = ![]() – монотонна при х > 0 ( зростає при a > 1 і спадає при 0< а < 1 ) і кожного свого значення набуває лише при одному значенні аргументу, то отримуємо, що на області визначення рівняння виду
– монотонна при х > 0 ( зростає при a > 1 і спадає при 0< а < 1 ) і кожного свого значення набуває лише при одному значенні аргументу, то отримуємо, що на області визначення рівняння виду ![]() =
= ![]() рівносильне рівнянню f (x) = g (x). Можна зробити висновок, що рівняння
рівносильне рівнянню f (x) = g (x). Можна зробити висновок, що рівняння![]() =
= ![]() рівносильне системі
рівносильне системі
![]() f (x) = g (x),
f (x) = g (x),
f (x) > 0,
g (x) > 0.
Наслідок. Нехай а > 0, а ≠ 1. Рівняння виду ![]() =
= ![]() рівносильне будь – якій із систем
рівносильне будь – якій із систем
![]()
![]() f (x) = g (x), або f (x) = g (x),
f (x) = g (x), або f (x) = g (x),
f (x) > 0. g (x) > 0.
Вибір відповідної системи, як правило пов’язаний з тим , яку з нерівностей ,
f (x) > 0 або g (x) > 0, розв’язати легше. Якщо обидві нерівності є складними, то алгоритм розв’язання буде таким: записуємо систему, розв’язуємо рівняння f (x) = g (x) та перевіряємо корені.
Приклад . Розв’яжіть рівняння: 1). ![]() ;
;
2). ![]() .
.
Розв’язання. 1). ![]() ;
;
![]()
![]()
![]() 3х – 5 = х – 3; 2х = 2; х = 1;
3х – 5 = х – 3; 2х = 2; х = 1;
х – 3 > 0; х > 3; х> 3. Відповідь. Розв’язків немає.
2). ![]() .
.
![]()
![]()
![]() х + 7 =
х + 7 = ![]() + 5; х2 – х – 2 = 0; х1 = - 1 ;
+ 5; х2 – х – 2 = 0; х1 = - 1 ;
х + 7 > 0 х > - 7 х2 = 2;
х > - 7 . Відповідь. – 1; 2.
3. Рівняння виду ![]() .
.
Рівняння виду ![]() рівносильне рівнянню f(x) =
рівносильне рівнянню f(x) = ![]() . Вираз
. Вираз ![]() > 0 тож умова f (x) > 0 виконується автоматично.
> 0 тож умова f (x) > 0 виконується автоматично.
Приклад № 6.30.
Розв’яжіть рівняння 1). ![]() ) = 3 – x.
) = 3 – x.
Розв'язання. ![]() ) = 3 – x;
) = 3 – x;
6 + ![]() =
= ![]() ; 6 +
; 6 + ![]() =
= ![]() ;
; ![]() + 6·
+ 6·![]() – 27 = 0;
– 27 = 0;
нехай ![]() = t, t > 0 тоді
= t, t > 0 тоді ![]() + 6t – 27 = 0 ,
+ 6t – 27 = 0 , ![]() = - 9,
= - 9, ![]() = 3.
= 3.
Тож ![]() = - 9 і
= - 9 і ![]() = 3. Рівняння
= 3. Рівняння ![]() = - 9 – немає розв’язків, а розв’язком рівняння
= - 9 – немає розв’язків, а розв’язком рівняння ![]() = 3, x = 1.
= 3, x = 1.
Відповідь. 1.
4. Рівняння, які зводяться до простих за допомогою властивостей логарифмів.
При розв’язанні складних логарифмічних рівнянь можна дотримуватися наступного алгоритму розв’язання рівнянь:
1). Знаходимо область допустимих значень рівняння.
2). За допомогою властивостей логарифмів зводимо рівняння до одного раніш розглянутих типів.
3). Розв’язуємо отримане рівняння, перевіряємо належність коренів області допустимих значень.
4). Даємо відповідь.
Приклад №6.23 Розв’яжіть рівняння:
1). ![]() = 2.
= 2.
Розв’язання.
![]() 1). Область допустимих значень знайдемо із системи:
1). Область допустимих значень знайдемо із системи:
![]() х + 1> 0, х > 1,
х + 1> 0, х > 1,
2х - 1> 0; х > ![]() ; х > 1.
; х > 1.
2). Використовуючи формулу ![]() +
+ ![]() =
= ![]() рівняння приймає наступний вигляд:
рівняння приймає наступний вигляд: ![]() = 2.
= 2.
3). Тоді ![]()
![]() ; 2
; 2![]() + х – 10 = 0;
+ х – 10 = 0; ![]() = - 2,5;
= - 2,5; ![]() = 2.
= 2.
Області допустимих значень задовольняє лише другій корінь.
Відповідь. 2.
2). ![]() = 2
= 2 ![]() -
- ![]() .
.
Розв’язання.
![]()
![]() 1). Область допустимих значень знайдемо із системи : 2х – 1 > 0, х >
1). Область допустимих значень знайдемо із системи : 2х – 1 > 0, х > ![]() ,
,
х – 4 > 0; х > 4;
х > 4
2). ![]() +
+ ![]() = 2
= 2 ![]() ;
;
![]() =
= ![]() ;
;
(2х – 1)( х – 4) = 9; 2![]() - 9 х – 5 = 0;
- 9 х – 5 = 0; ![]() = -
= -![]() ;
; ![]() =5
=5
Області допустимих значень задовольняє лише другій корінь.
Відповідь. 5.
5. Заміна змінних у логарифмічних рівняннях.
Часто логарифмічні рівняння зводяться до алгебраїчних заміною t = ![]()
Приклад. № 6.25(1) Розв’яжіть рівняння : log72(x + 1) - 2![]() – 3= 0.
– 3= 0.
Розв’язання.
1) Нехай ![]() = t, тоді маємо рівняння
= t, тоді маємо рівняння
![]() – 2t – 3 = 0;
– 2t – 3 = 0; ![]() = -1;
= -1; ![]() = 3.
= 3.
2) ![]() = - 1; х + 1 =
= - 1; х + 1 = ![]() ; х =
; х = ![]() – 1;
– 1; ![]() = -
= - ![]() або
або
![]() = 3; х +1 =
= 3; х +1 = ![]() ; х = 343 – 1;
; х = 343 – 1; ![]() = 342.
= 342.
Відповідь. - ![]() ; 342.
; 342.
ІV. Застосування нових знань і способів дій.
Розв’яжіть рівняння за допомогою означення логарифма ( усно):
-
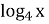 = 3; 2).
= 3; 2). 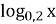 =- 2; 3).
=- 2; 3). 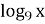 =
= 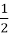 ; 4).
; 4). 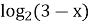 =0;
=0;
5) ![]() = -2
= -2
Розв’яжіть рівняння :
№ 6.9(1) log32x + 2 ![]() – 3 = 0.
– 3 = 0.
Розв’язання.
log32x + ![]() – 3 = 0.
– 3 = 0.
Нехай ![]() = t , тоді маємо рівняння
= t , тоді маємо рівняння ![]() + 2t – 3 = 0,
+ 2t – 3 = 0, ![]() = -3 ,
= -3 , ![]() = 1.
= 1.
![]() = -3; x =
= -3; x = ![]() ; x1 =
; x1 = ![]() або
або ![]() = 1; x =
= 1; x = ![]() ; x2 = 3.
; x2 = 3.
Відповідь. ![]() ; 3.
; 3.
№6.15(2) 5 ![]() -
- ![]() = 9.
= 9.
Розв’язання.
5 ![]() -
- ![]() = 9.
= 9.
Використовуючи формулу ![]() = p
= p![]() рівняння приймає наступний вигляд:
рівняння приймає наступний вигляд: ![]() - 4
- 4![]() = 9;
= 9;
- 3![]() =9;
=9; ![]() = - 3; x =
= - 3; x = ![]() ; x =
; x = ![]() .
.
Відповідь. ![]() .
.
V. Домашнє завдання: §6 опрацювати матеріал.
Виконати завдання №6.8, №6.10, №6.20.


про публікацію авторської розробки
Додати розробку
