Урок алгебри в 11 класі на тему; Логарифмічна функція"

Тема уроку:  Логарифмічна функція.

(Для класів з поглибленим вивченням математики)

Мета уроку:

освітні: сформувати у учнів поняття логарифмічної функції, навчитись будувати її графік;

развиваючі: развивати увагу, пам'ять і логічне мислення;

виховні: виховувати акуратність при побудові графіків, інтерес до предмету.

Знання і вміння:
 

• 
  учні повинні знати означення логарифмічної функції;
• 
  вміти будувати її графік;
• 
  знати історію створення логарифмів.

Тип уроку: комбінований.

 

Хід уроку
 

1. 
   Вчитель: Добрий день, діти! Сьогодні ми дізнаємось, що є логарифмічна функція, який вигляд має її графік.
2. 
   Вчитель: Давайте з вами згадаємо, що називається логарифмом числа?

Учень: Логарифмом числа b за основою а называется показник степеня, до якого потрібно піднести основу а, щоб отримати число b.

^ Вчитель: Як називають формулу = b (де b > 0, а > 0, a  l)?

Учень: Формулу = b (где b > 0, а > 0, a  l) називають основною логарифмічною тотожністю.

Вчитель:Які ви знаєте властивості логарифмів?

Учень: (пише на дошці):

1 = 0

2 = 1

3 

4 

5 

Вчитель: Як виглядає формула переходу від однієї основи логарифма до іншого?

Учень: (пише на дошці): 
 

3. 
   Запишіть в зошиті тему сьогоднішнього уроку «Логарифмічна функція».

Діти, ознайомтесь з історією створення логарифмів. 

Протягом XVI с. різко виріс об’єм роботи, пов'язаний з проведенням наближених обчислень при розв’язанні різних задач, і в першу чергу задач астрономії, яка має безпосереднє практичне застосування(зокрема, при визначенні положення судів по зіркам і Сонцю). Найбільші проблеми виникали, як неважко зрозуміти, при виконанні операцій множення і ділення. Спроби часткового спрощення цих операцій шляхом зведення їх до додавання (була складена, наприклад,таблиця квадратів цілих чисел від  1 до 100 000, яка дозволяла обчислювати добутки за формулою ab=(a + b)² – (a – b)²) великого успіху не мали. Тому відкриття логарифмів, яке зводило ділення і множення чисел до додавання і віднімання їх логарифмів, подовжило, по висловленню, Лапласа,життя обчислювачів.

логарифми надзвичайно швидко ввійшли в практику. Винахідники логарифмів не обмежились розробкою нової теорії. Було створено практичний засіб-таблиці логарифмів,- які стрімко підвищили продуктивність праці обчислювачів. Уже в 1623 р., тобто всього через 9 років після видання перших таблиць, англійським математиком Д. Гантером була винайдена перша логарифмічна лінійка, ставша робочим інструментом для багатьох поколінь. (До останнього часу, коли на наших очах широке розповсюдження отримала електрона обчислювальна техніка і роль логарифмів як засобу обчислення різко знизилась.)

Перші таблиці логарифмів складені незалежно один від одного шотландським математиком Дж. Непером (1550-1632) і швейцарцем И. Бюрги (1552-1632). В таблиці Непера,видані в книгах под назвами «Описання вражаючої таблиці логарифмів» (1614 г.) і «Будова вражаючої таблиці логарифмів» (1619 р.), увійшли значення логарифмів синусів, косинусів и тангенсів для кутів від 0 до 90° з кроком в 1 минуту. Бюрги підготував свої таблиці логарифмів чисел,очевидно, до 1610 р., але вийшли в світ вони в 1620р., вже після видання таблиць Непера,і тому залишились непоміченими.

Одна з важливих ідей, яка лежала в основі винаходу логарифмів, була вже відома. Штифель (1487-1567) і ряд інших математиків звернули увагу на те, що множенню і діленню членів геометричної  прогресії

..., а^–3, а^–2, а^–1, 1, а, а², а³, ...

відповідають додавання і віднімання показників, які утворюють арифметичну прогресію

..., –3, –2, –1, 0, 1, 2, 3, ... .

Але однієї цієї ідеї недостатньо. Наприклад, «сіть» цілих степенів числа 2 занадто рідка; багато чисел «залишаються без логарифмів», тому необхідна була ще одна ідея: підносити до степеня числа, дуже близькі до одиниці. Помітивши, що, що степені і  при великих значеннях п близкі, Непер і Бюрги прийняли аналогичне рішення: Непер брав в якості основи число , а Бюрги – число .

Подальший хід їх думки і опис схем обчисленб переказати досить важко тому, що маємо багато непростих деталей і тому, що взагалі тексти XVI с.досить туманні. Уточню лише, що фактично надалі Непер переходить до основи . а Бюрги – до основик . Це не змінило суті справи (як вам відомо, , і тому вказані переходи приводять лише до перенесення коми в логарифмі), але дозволило достатньо спростити обчислення і самі таблиці.

Таким чином, по суті обидва винахідника логарифмів прийшли до висновку про доцільність розглядання степенів вигляду , ге ^М дуже велике число. Розгляд чисел такого виду приводить до відомого вам числа е, яке визначається як . Залишилось вже недовго до ідеї прийняття в якості основи логарифма числа е (основа таблиці логарифмів Бюрги співпадає з точністю до третього знаку з е,  основа таблиці логарифмів Непера близке до  числа .

Перші таблиці десяткових логарифмів (1617 г.) були складені за порадою Непера англійським математиком Г. Бриггсом (1561-1630). Багато з них були знайдені за допомогою виведеної Бриггсом наближеної формули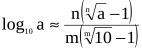



достатньо точної при великих значення т и п. Бриггс брав значення т і п у вигляді степенів двійки: це давало йому можливість звести обчисленн  і до послідовного виділення квадратних коренів.

Друга ідея Бриггса дозволяє знаходити значення десяткових логарифмів деяких чисел самостійно, без допомоги таблиць. Ціла частина логарифма цілого числа на одиницю менше кількості цифр в самому числі. Тому, наприклад, для знахождення lg 2 з точністю до трьох знаків достатньо знайти число цифр . Це не дуже важко.

х і у.При складанні таблиць логарифмів важливу роль зіграло знайдене Непером и Бюрги співвідношення між приростом у вдовільній точці х₀ для функції y = log_ax. Не вдаючись в деталі їх системи викладення, основний результат можна подати так: , де k – деяка константа. Якщо основа логарифмів– степінь J , де п – достатньо велике число, то .

Спрямовуючи х до нуля, приходимо до диференціального рівняння у'=, розв’язанням якого, як ви знаєте, являється функція ln x + C. Існує система викладення, при якій ln х₀ з самого початку визначається як , тобто ln х₀ – площа криволінійної трапеції, обмеженої гіпербдлдю, віссю абсцис і прямими х = 1 и х = x₀. Виведення відомих вам властивостей логарифмів, виходячи з цього означення, не дуже проста, але доступна вам задача.

Нехай а – додатне число, яке не дорівнює 1.

Визначення. Функцію, задану формулою 

y = log_a x, (1)

называють логарифмічною функцією з основою а.

Перечислимо основні властивості логарифмічної функції.
 

1. 
   Область визначення логарифмічної функції– множина всіх додатних чисел R₊, тобтоD(log_a) = R₊.
2. 
   Область значень логарифмічної функції – множина всіх дійсних чисел.
3. 
   Логарифмічна функція на всій області визначення зростає (при a > 1) або спадає (при 0 < a < 1).

Справедливе наступне твердження:

Графіки показникової і логарифмічної функцій, які мають одну основу, симетричні відносно прямої у = х (див. рис. 1).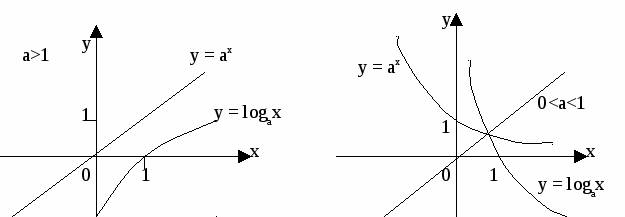


a) б)

Рис. 1. Графіки показникової і логарифмічної функцій
Приклад 1. Знайти область визначення функції f(x) – log₈(4-5x).

Область визначення логарифмічної функції множина R₊. Тому задана функція визначена тільки для тих х, при яких 4 – 5х > 0, тобто при x <  0,8. Тому областю визначення заданої функції являється інтервал (–;0,8).

Приклад 2. Порівняти числа log₃5 і log₃7. Логарифмічна функція з основою, більшою за 1, зростає на всій числовій прямій. Оскільки 7 > 5, то log₃7 > log₃5.
 

4. 
   Виконаємо деякі вправи:
   №1. Знайти область визначення виразу:
   
   а) log₅(9 – х²) б)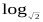 (х² – 2х – 3)
   
   Ррозв’язання:
   
   а) Вираз визначено при всіх тих х, при яких 9 – х² > 0. Ррозв’язуючи цю квадратну нерівність, маємо, що ррозв’язанням являється (– 3; 3).
   
   
   
   б) аналогічно а) х² – 2х – 3 > 0
   
   
   
   Відповідь: (– ;–1)) (3;+
   
   №2. Порівняти числа:
   
   а) log₂3,8 і log₂4,7 б)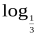 0,15 і 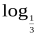0,2 в) log₂10 і log₅30.
   
   Розв’язання
   
   а) Оскільки 2>1, то log₂3,8 < log₂4,7
   
   б) Оскільки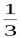 <1, то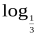0,15 > 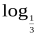0,2
   
   в) 
   
   
    

5. 
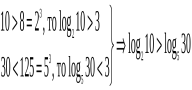
   Отже, ми з вами познайомились з історією створення логарифмів, дізнались, що є логарифмічною функцією, який її графік, навчились виконувати вправи, пов’язані з логарифмічною функцією.
6. 
   Домашнє завдання: 

1) знати область визначення логарифмічної функції, її властивості; 

2)знайти область визначення виразів:

а) (6 + х – х²) б) log_0,3(х² – 16)

3) Порівняти числа:

а) log₃5,1 і log₃4,9 б) 1,9 і 2,5 в) log₃10 і log₈57.