Урок "Математика і мистецтво"

Математика і мистецтво. Точність, гармонія і краса.

                             ( для учнів 9 класу )

Епіграф уроку:

«... Геометрія володіє двома скарбами - теоремою Піфагора і золотим перерізом , і якщо перше з них можна порівняти з мірою золота , то друге - з коштовним каменем ... »    Йоганн Кеплер.

МЕТА:  

- Розширити кругозір учнів , сприяти розвитку пізнавального інтересу .

-Показати школярам загально - інтелектуальне значення математики .

- Сприяти пізнання законів краси і гармонії навколишнього світу.

.ОБЛАДНАННЯ: роздатковий матеріал (задачі про золотий переріз)

                               Презентація «Золотий переріз у мистецтві»

                             „Правильні многокутники”;

           фотографії пам”яток архітектури;

І. Організаційний момент.

ІІ. Перевірка д/з

ІІІ. Розв’язування задач

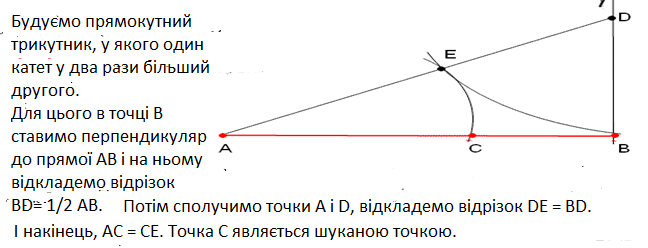
Задача1.  Поділити відрізок АВ точкою С так, щоб

Побудова

Задача2. Виміряємо у см довжини відрізків і знайдемо відношення

Висновок: У нас вийшло число ɥ ≈1,62.

Таке відношення і буде золотим, а такий переріз – золотим перерізом.

Вчитель математики                                                                                                                        Навколишній світ різноманітний ...

Ви, напевно, звертали увагу, що ми неоднаково ставимося до предметів і явищ навколишньої дійсності. Безладність, безформність, неспівимірність сприймаються нами як потворне і виробляють відразливе враження. А предмети та явища, яким властива міра, доцільність і гармонія сприймаються як гарне й викликають у нас почуття захоплення, радості, піднімають настрій. Людей з давніх часів хвилювало питання, чи підкоряються такі  речі, як краса і гармонія, яким-небудь математичним розрахункам. Чи можна « перевірити алгеброю гармонію». Звичайно, всі закони краси неможливо вмістити в кілька формул, але, вивчаючи математику, ми можемо відкрити деякі складові прекрасного.

Сьогодні на уроці ми познайомимся з одним з таких математичних співвідношень, і там, де воно присутнє, відчувається гармонія і краса. Теорему Піфагора знають багато людей, а от що таке              «золотий переріз» - далеко не всі.

Що ж таке золотий переріз ? Слово „переріз” означає поділ відрізка на дві частини. Золотим же назвали його тому, що там де він присутній відчувається гармонія і краса.

Учень. Під золотим перерізом мають на увазі знаходження на даному відрізку АВ такої точки С, щоб виконувалось співвідношення

АВ:АС=АС:СВ, щоб більша частина відрізка, яка відтинається точкою С, була середньою пропорційною величиною між усім відрізком та меншою його частиною.

Вчитель мистецтва. (Презентація)

Золотий переріз в мистецтві

   На перший погляд такий поділ відрізка здається дуже складним і рідкісним, але це не так.

 Золотий переріз широко використовується в теорії і практиці мистецтва скульптури, в живописі.

  Середньовічний монах і математик Лука Пачоллі у 1509 році написав трактат „Про божественну пропорцію”, а ілюстрації до книги виконав Леонардо да Вінчі. Він переконаний, що пропорція існує скрізь: у математиці і механіці, у медицині та географії, в усіх інших науках. Особливу роль відіграє золотий переріз у мистецтві, живописі, скульптурі. Розглянемо скульптуру Аполона, яку вважають еталоном чоловічої краси. Якщо її висоту поділити у відношенні золотого перерізу і це ж саме проробити з кожною частиною тіла, то точки ділення попадають на анатомічно важливі місця: початок шиї, талію, коліно. Ця ж закономірність поширюється на руки і обличчя.

Золотий переріз в архітектурі

 Тільки дотримуючись законів геометрії, архітектори змогли створити свої шедеври. Пропорція в архітектурі-це ніби її внутрішня краса. Вона невидима безпосередньо, але завжди відчутна як і краса духовна. Особливо велику роль відіграє золотий переріз в архітектурі. Фасад одного з найкращих витворів давньогрецьких архітекторів-Парфенона-храм богині Афіни, побудований у 5 ст. до н. е. в Афінах.

На основі золотого перерізу створена Капелла Пацци у Флоренції. Золотий переріз використано при побудові багатьох споруд з колонадами, фрагментів архітектури у Києві

(Можна дати учням фотографії).

Вчитель математики.

Давайте повторимо з вами про багатокутники.

1. Назвіть відомі вам багатокутники.
2. Завдання. Знайти внутрішній кут правильного п’ятикутника.

Сума внутрішніх кутів: 180·(5-2) = 540.

Кожен кут: 540:5=108 градусів.

(Тут можна використати як за допомогою орігамі зробити п’ятикутник).

Чудовий приклад «золотого перерізу» являє собою пентаграма - правильний п'ятикутник. Зірка – вона відома. Форму п'ятикутної зірки мають багато квітів, морські зірки і їжаки, віруси і т. д.  Людське тіло також можна розглядати як п'ятипроменеву фігуру, де променями служать голова, руки і ноги. Перші згадки про пентаграму  відносяться до Стародавньої Греції. У перекладі з Грецького пентаграма означає дослівно п'ять ліній ( leuta - п'ять , gramma - риса, лінія). У еллінському світі наука і мистецтво розвивалися в так званих філософських школах.

Однією з найвідоміших серед них була школа Піфагора, а відмінним знаком її членів була пентаграма. Піфагорійці відрізнялися винятковою вірністю своєму братству.

Учень розповідає легенду.

Збереглася легенда, згідно з якою один з піфагорійців, тяжко захворівши на чужині, і залишившись без засобів існування, попросив господаря будинку, залишити його, намалювавши на воротах пентаграму. Коли повз будинку проходив інший  піфагорієць, і на воротах він побачив пентаграму він щедро розплатився з господарем.

Звичайно, піфагорійці не випадково вибрали пентаграму. Вони вважали, що цей красивий багатокутник має багато  містичних  властивостей. Саме пентаграма була символом життя і здоров'я, їй присвоювалась здатність захищати людину від злих духів.

Вчитель математики. Чим же цікавий цей символ з точки зору математики? Пентаграма представляє собою вмістилище золотих пропорцій! З подібності трикутників ACD і ABE можна вивести відому пропорцію. Цікаво, що всередині п'ятикутника можна продовжити будувати п'ятикутники, і золоті відношення будуть зберігатися.

Практична робота. (можна дати цю практичну роботу учням виконати вдома ще напередодні уроку, а на уроці тільки зробити висновки.)

У 1855 р. німецький дослідник золотого перерізу професор Цейзінг опублікував свою працю «Естетичні дослідження». Він виміряв близько двох тисяч людських тіл і дійшов висновку, що пропорції золотого перерізу проявляються в відношенні частин тіла людини - довжина плеча , передпліччя і кисті, кисті і пальців і т.д. Ділення тіла точкою пупа - найважливіший показник золотого перерізу .

Результати вимірювань учнів класу.

Учням класу було запропоновану роботу, вони повинні були провести вимірювання висоти і довжину від пупа до ніг, результати заносимо у  таблицю .

Висновок: пропорції тіла людини приблизно дорівнює показнику золотого перерізу, що підтверджує теорію Цейзинга .

Підсумки уроку:

Отже:

Що найбільше сподобалося?

Що запам'яталося найбільше?

Я думаю, що ви запам'ятали, де використовується золотий переріз в мистецтві, і як результат, зможете побачити золоту пропорцію в оточуючих нас предметах.

Вчитель мистецтва.

У книзі "Математика і мистецтво" А. В. Волошинов пише: "Мистецтво - самостійна галузь культури, воно виткане з діалектично протилежних начал - матеріального і духовного, розрахованого та вгаданого. Воно доступне точному математичному аналізу в першій частині. Але у другій - до неї треба прислухатися душею. Але краса є не лише в мистецтві. Краса - усюди. Є вона і в науці, і особливо в її перлини - математики. Пам'ятайте, що наука на чолі з математикою відкриє перед нами казкові скарби краси.

Перегляд відеоролика «Що спільного?»

Домашнє завдання.

Знайти в інтернеті ще використання золотого перерізу (музика, анатомія людини, природа, тощо).

Дякуємо за урок.