Урок математики у 6 класі "Пропорція. Основна властивість пропорції."
Тема уроку. Пропорція. Основна властивість пропорції.
Мета уроку. Ознайомити учнів з означенням та властивістю пропорції; формувати вміння й навички застосування її до розв'язування вправ; розглянути приклади використання пропорції у практичному житті.
Розвивати в учнів пізнавальний інтерес, інформаційні компетенції, формувати навички взаємоконтролю і самоконтролю.
Виховувати інтерес до предмету; працьовитість, наполегливість, охайність ведення записів; вміння об'єктивно оцінювати результати індивідуальної роботи.
Математика, 6 клас
Тема уроку. Пропорція. Основна властивість пропорції.
Мета уроку. Ознайомити учнів з означенням та властивістю пропорції; формувати вміння й навички застосування її до розв’язування вправ; розглянути приклади використання пропорції у практичному житті.
Розвивати в учнів пізнавальний інтерес, інформаційні компетенції, формувати навички взаємоконтролю і самоконтролю.
Виховувати інтерес до предмету; працьовитість, наполегливість, охайність ведення записів; вміння об’єктивно оцінювати результати індивідуальної роботи.
Тип уроку: урок засвоєння нових знань.
Очікувані результати: учні повинні
знати означення пропорції і члени пропорції; основну властивість пропорції;
вміти складати пропорції; знаходити невідомий член пропорції.
Хід уроку.
І. Повторення вивченого.
1. Усне опитування (слайди презентації)
- Що вивчали на минулому уроці? Давайте заповнимо пропуски:
Відношенням двох чисел називається______________________________;
Відношення показує, у скільки ___________________________________;
Відношення _______________, якщо кожне з чисел помножити ____________ на відмінне від 0 число.
Щоб знайти відношення двох чисел, треба ці числа ___________.
2. Перевірка домашнього завдання.
№ 515 Знайти відношення чисел:
-
3 км : 4 км =
 ;
;
-
18 ц : 6 ц =
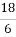 = 3;
= 3;
-
100 м : 1 км = 100 м : 1000 м =
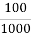 =
= 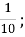
- 1 год : 10 хв = 60 хв : 10 хв = 6;
-
15 кг : 250 г =
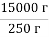 = 60 ;
= 60 ;
-
20 см2 : 1 дм2 = 20 см2 : 100 см2 =
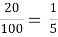
Питання до класу:
Що треба було згадати, щоб виконати приклади 3, 4, 5, 6?
№ 521 Замінити відношення дробових чисел відношенням натуральних чисел:
-
4 :
 =
= 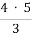 =
= 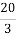 = 20 : 3;
= 20 : 3;
-
 :
:  =
=  =
=  = 4 : 5;
= 4 : 5;
- 1,8 : 0,4 = 18 : 4 = 9 : 2;
-
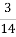 : 1
: 1  =
= 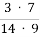 =
=  = 1: 6
= 1: 6
Питання до класу: як поділити дріб на дріб?
3. Усні вправи.
1)Прочитати відношення та назвати його члени: 8 : 9; 3 : 4; ![]()
2)Спростити відношення: 24 : 36; 35 : 105; 1800 : 100
3)Знайти відношення чисел: 2,4 : 1,2; 10 : 20; 15 : 60; 3,5 : 0,7; ![]() :
: ![]()
4)Як зміниться відношення, якщо попередній член відношення збільшити у 2 рази? Наступний член відношення збільшити у 3 рази?
4. Самостійна робота (індивідуальні картки )
а) знайти відношення чисел: 1,8 : 7,2
2,8 : 0,07
4 дм : 8 см
б)замінити відношенням цілих чисел: а) 2 : ![]() ; б)
; б) ![]() :
: ![]() ; в)
; в) ![]() :
: ![]()
ІІ. Мотивація навчальної діяльності
На дошці записано декілька відношень:
![]()
![]()
![]()
![]()
![]()
![]() Знайти рівні відношення та записати рівності у зошит.
Знайти рівні відношення та записати рівності у зошит.
У математиці рівним відношенням дали назву – пропорція . Слово «пропорція» означає відношення частин між собою. Стародавні греки називали вчення про відношення і пропорції музикою, яку вважали галуззю математики. Вони дуже полюбляли грати на різних музичних інструментах. Особливо на тих, які мають струни. І щоб ці струни звучали узгоджено, приємно для нашого слуху, треба, щоб їх довжина і товщина перебували у певному відношенні, тобто у певній пропорції. Тому вчення про відношення вони називали музикою.
Інший приклад. Один чоловік вирішив побудувати будинок. Ось перед вами два проекти, виконані архітекторами. Матеріальні затрати однакові, а зовнішньо вони відрізняються. Допоможіть вибрати кращий будинок. У якому з них ви б хотіли жити? Чому? Чи змогли б ви жити у будинку, де вікна різної форми та розмірів, димохід встановлено похило? Кажуть, що в такому будинку немає гармонії і немає пропорції. Отже, тема нашого уроку «Пропорція». Ми навчимося читати пропорцію, знати назву її членів, знаходити члени пропорції.
ІІІ.Засвоєння нових знань
- Пояснення матеріалу
Запишемо пропорцію в загальному вигляді ![]() =
= ![]() або а : b = c : d
або а : b = c : d
Сучасний запис пропорції ввів німецький математик Лейбніц, який жив 300 років тому. А тепер запишемо наші пропорції у рядок:
49 : 7 = 35 : 5
3 : 6 = 15 : 30
6 : 18 = 10 : 30
Із скількох чисел складається пропорція?
Чи порушиться пропорція, якщо я переставлю числа у будь-якій парі (лівій чи правій)? Отже, кожне число у пропорції знаходиться на своєму місці. І тому вони мають свої назви. Члени пропорції, які знаходяться по краям пропорції, називаються крайніми членами, а ті, що знаходяться у середині пропорції – середніми. Називаємо члени пропорцій, які ми щойно записали.
2.Формування первинних вмінь та навичок
а) Записати пропорції: 7 : 2 = 14 : 4
2 : 3 = 10 : 15
2 : 5 = 8 : 20
Назвати члени пропорції.
Учні називають, вчитель вписує їх у таблицю:
|
Крайні члени пропорції |
Середні члени пропорції |
|
7 і 4 |
2 і 14 |
|
2 і 15 |
3 і 10 |
|
2 і 20 |
5 і 8 |
Уважно придивіться на ці пари. Що цікавого є у цих парах? Так, помітили, що добутки кожної пари з пропорції однакові. Зробимо висновок: у пропорції добуток середніх її членів дорівнює добутку крайніх. Це і є основна властивість пропорції.
б) Користуючись основною властивістю пропорції, зясувати, чи можна з даних відношень скласти пропорцію:
6 : 4 та 0,3 : 0, 2
1 : 6 та 5 : 30
4 : 7 та 6 : 5
Чи порушиться пропорція, якщо я поміняю місцями крайні члени? Середні члени?
3.Дослідницька робота
Складемо правило для знаходження невідомого члена пропорції:
Х : 12 = 5 : 10 скористаємося основною властивістю пропорції
10х = 60
Х = 60 : 10
Х = 6 (над числами пишемо букви к і с) учні роблять висновок та складають правило знаходження невідомого крайнього. Аналогічно
![]() =
= ![]() Складаємо правило, промовляємо разом, потім проговорюємо один одному у парах.
Складаємо правило, промовляємо разом, потім проговорюємо один одному у парах.
ІV. Підсумок уроку.
Як багато цікавого і корисного ми дізналися.
Розгадування кросворда. 1. Як називаються члени пропорції, які знаходяться скраю?
- Скільки чисел утворюють пропорцію?
- Стародавні греки порівнювали пропорцію з чим? (музика)
- Як називаються члени пропорції, які знаходяться в середині? (середні)
- Яким словом можна замінити слово «відношення»? (частка)
|
|
1 |
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
|
||||
|
3 |
|
|
|
|
|
|
|||||
|
|
4 |
|
|
|
|
|
|
||||
|
5 |
|
|
|
|
|
|
|||||
Чому ж ми пов’язуємо слово «краса» з темою уроку?
Правильно, адже пропорція – це краса в музиці, в архітектурі, у техніці, скрізь, де дотримано правильного відношення, де досягається справжня гармонія.


про публікацію авторської розробки
Додати розробку
