ДАТА                                                                                                          група/клас

Тема уроку: Властивості тригонометричних функцій.

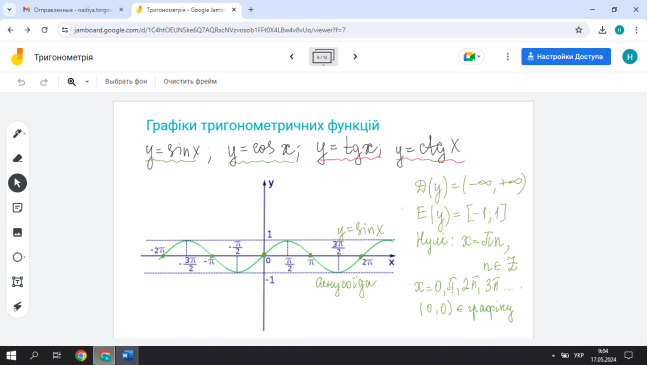
Мета уроку: Вивчення властивостей тригонометричних функцій у = sin х,         у = cos х, у = tg х, у = ctg x, а саме: область визначення; область значень; парність (непарність); симетричність графіків; періодичність; нулі; проміжки спадання (зростання); проміжки знакосталості; найбільші і найменші значення.

Форма проведення: дистанційно, синхронний режим, конференція в Google Meet.

Обладнання: Ноутбук, мобільні пристрої в здобувачів освіти.

І. Перевірка домашнього завдання. Вибірково перевірити з поясненнями здобувачів.

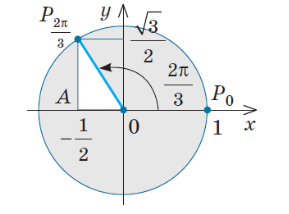II. Вивчення властивостей тригонометричних функцій.

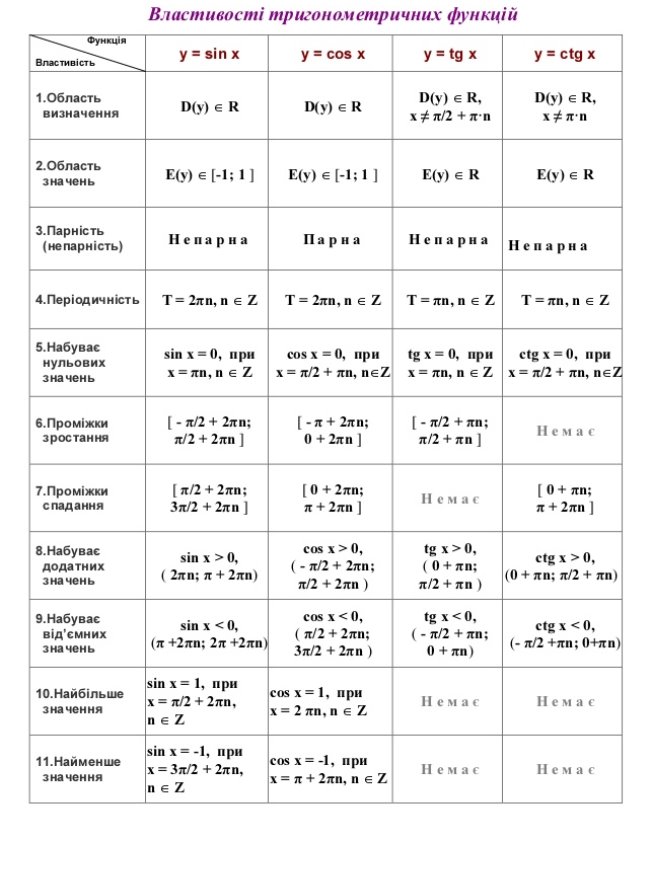
Властивості вивчених тригонометричних функцій зручно за­писати в таблицю. При заповненні таблиці мож­ливі такі коментарі:

1. Вирази sin х і cos х визначені для будь-яких x, оскільки для будь-якого числа х можна знайти координати точки , оди­ничного кола.

Вираз tg х має смисл при будь-якому x, крім чисел виду х = , n Ζ.

Вираз ctg x має смисл при будь-якому x, крім чисел виду х = πп, n Ζ.

2. Оскільки sin х і cos х — це ордината і абсциса точки одиничного кола, то областю значення синуса і косинуса є про­міжок [-1; 1].

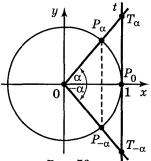
Оскільки tg α — це ордината точки лінії тангенсів, то обла­стю значень тангенса є R.

Оскільки ctg α — це абсциса точки лінії котангенсів, то областю значень котангенса є R.

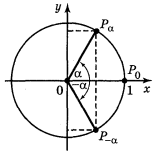
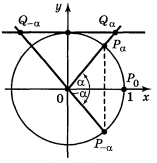
3. Оскільки точки Р_α і Р_-α одиничного кола симет­ричні відносно осі ОХ, то ці точки мають однакові абсциси і про­тилежні ординати, тобто       sin (-α) = -sin α; cos (-α) = cos α.

III. Застосування властивостей тригонометричних функцій до розв'язування вправ (робота з дошкою Jamboard, посилання: https://jamboard.google.com/d/1C4htOEUNSke6Q7AQRscNVzvosob1FFt0X4LBw4v8vUo/edit?usp=sharing

Виконання вправ

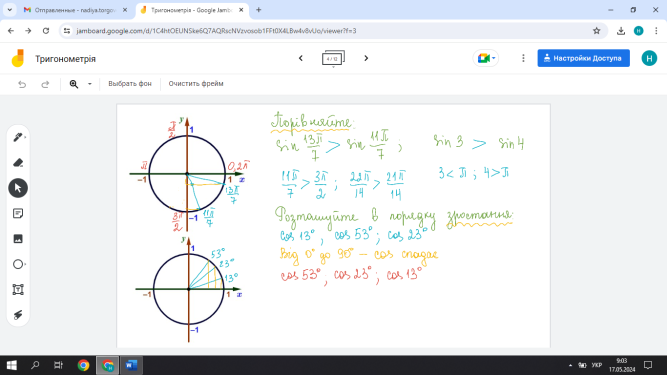
1. Використовуючи властивості функції у = sin x, порівняйте числа:

a) sin і sin ;  б) sin і sin ;  в) sin 3 і sin 4;   г) sin 1° і sin 1.

Відповідь: a) sin > sin ;  б)  sin > sin ;

   в) sin 3 > sin 4;           г) sin 1° < sin 1.

2. Розташуйте числа в порядку зростання:

a) sin 20°; sin 85°; sin 30°;

б) sin 0,2; sin 0,3; sin 0,1; в) sin 2; sin (-2); sin (-1); sin 1.

Відповідь: a) sin 20°; sin 30°; sin 85°;

  б) sin 0,1; sin 0,2; sin 0,3;  в) sin (-2); sin (-1); sin 1; sin 2.

3. Використовуючи властивості функції у = cos x, порівняйте числа:

1.      cos 2,52 і cos 2,53; б) cos (-4,1) і cos (-4); в) cos 1 і cos 3; г) cos 4 і cos 5.

Відповідь: a) cos 2,52 > cos 2,53;   6) cos (-4,1) > cos (-4);

   в) cos 1 > cos 3;          г) cos 4 < cos 5.

4. Розташуйте числа в порядку зростання:

a) cos 13°; cos 53°; cos 23°;   б) cos 0,3; cos 0,6; cos 0,9; в) cos 2; cos 4; cos 6. Відповідь: a) cos 53°; cos 23°; cos 13°; б) cos 0,9; cos 0,6; cos 0,3;

в) cos 4; cos 2; cos 6.

5. Використовуючи властивості функції у = tg x, порівняйте чис­ла:

а) tg (-2,6π) і tg (-2,61π);  б) tg 2,7π і tg 2,75π; в) tg 2 і tg 3; г) tg 1 і tg 1,5.

Відповідь: а) tg (-2,6π) > tg (-2,61π);   б) tg 2,7π < .tg 2,75π;

   в) tg 2 < tg 3;    г) tg 1 < tg 1,5.

6. Розташуйте числа в порядку зростання:

a) tg 25°; tg 65°; tg 15°;     б) tg (-1); tg (-2); tg (-3);     в) tg (-5); tg (-3); tg 3.

Відповідь: а) tg 15°; tg 25°; tg 65°;   б) tg (-1); tg (-3); tg (-2);

  в) tg 3; tg (-3); tg (-5).

IV. Підсумок уроку.

V. Домашнє завдання.

§ 9, ст. 84-90, виконати № 9.8, 9.10. Посилання на підручник:  https://cutt.ly/jCpzrRN