Урок "Медіана, бісектриса, висота трикутника"

Тема уроку: Медіана, бісектриса, висота трикутника.
Мета:  ознайомити учнів із поняттями: медіана, бісектриса, висота трикутника; сформувати вміння   зображувати ці відрізки та розрізняти їх, виходячи з умов задачі; розвивати логічне мислення, увагу, пам’ять, уміння чітко та математично грамотно виражати свою думку; виховувати працьовитість, акуратність.

Обладнання і наочність: презентація до уроку, заготовки трикутників.

Тип уроку: засвоєння нових знань та формування вмінь.

Хід уроку

1. Організаційний етап.

2. Перевірка домашнього завдання.

Учні здійснюють самоперевірку домашнього завдання . Розв'язання завдань подано на слайді.

№368

12>6+5 – неможливо ;11=6+5-неможливо

№391

1.7+9=16(см),  20-16=4(см) , 9<7+4 –можливо.

2.32-16=16(см), 16= 9+7- неможливо

3.18-16=2(см),  9=7+2- неможливо.

№415

х<2,8+0,6, х=3(см).

3. Актуалізація опорних знань.

Фронтальне опитування за технологією «Мікрофон».

1)Сформулювати означення трикутника.

2)На зображенні трикутника вказати вершини, сторони, кути трикутника.

3)У трикутнику ABC назвіть:

а) кути, прилеглі до сторони BC;

б) кут, протилежний стороні AC;

в) сторону, протилежну куту А;

г) сторону, протилежну куту С;

д) сторони, прилеглі до кута В.

3)Назвати види трикутників за сторонами та кутами.

4) Сформулювати теорему нерівності трикутників.

4.Мотивація навчальної діяльності.

Слово вчителя:

Окрім сторін та кутів трикутника існують інші елементи трикутника, які використовуються для розв’язування задач.

Отже, мета цього уроку: вивчити означення нових елементів трикутника та навчитися їх розпізнавати на рисунках та вміти будувати.

5.Сприйняття та усвідомлення  нового матеріалу.

Цікаво, що  відрізок, що з'єднує вершину трикутника з деякою точкою на протилежній стороні колись називали чевіаною. Тоді наприклад, висота – чевіана, опущена під прямим кутом  на протилежну сторону трикутника.

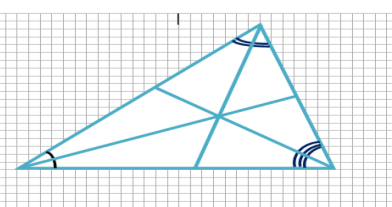
Інцентром трикутника називається точка перетину трьох його бісектрис.

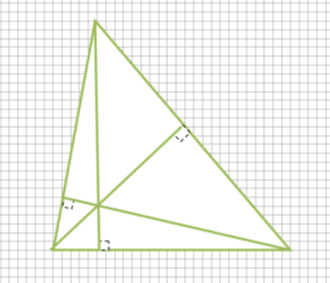
Точка перетину висот трикутника називається ортоцентром.

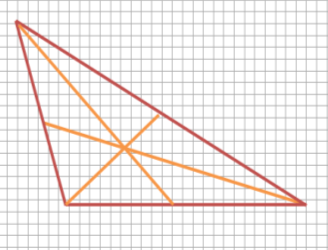
    Центроїдом трикутника називається точка перетину            його  медіан.

ЗАГАДКА МЕДІАНИ АБО ЗАДАЧА АРХІМЕДА

Твердження про те,що у кожному трикутнику три медіани перетинаються в одній точці було доведено ще Архімедом. Вчений показав, що центроїд трикутника – це точка, де зосереджена уся його маса. Тому цю точку ще називають центром мас, або центром ваги.

Давньогрецький математик,

фізик,інженер, винахідник

та астроном Архімед

6.Розв'язування вправ.

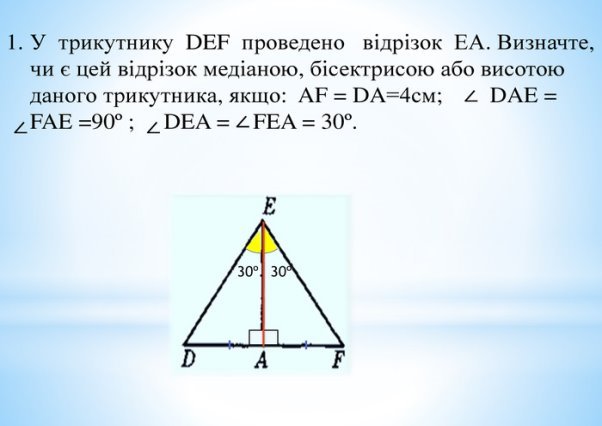
Колективне розв'язування задач під керівництвом учителя.
1.Практичні вправи. №132 , №135,136.
№140

5х+11х=80

16х = 80

х=5

5*5=25 (см), 7*5=35 (см), 11*5 =55 (см).

Відповідь: 25см, 35 см, 55см.

№149

ВD – спільна сторона для двох трикутників. Р∆АВС=(32+36)-20=48(см).

2.Практичне завдання: у моделі трикутника, щоб перевірити твердження Архімеда проведіть медіани. Якщо правильно виконали побудову усі три відрізки перетнуться в одній точці. Тут зосереджена уся маса фігури, тому цю точку називають центром мас фігури.

Якщо паперовий трикутник закріпити у цій точці або підвісити на нитці за неї, то фігура буде розташована горизонтально.

7. Підбиття підсумків уроку.
Фронтальне опитування .

1.Що таке медіана, бісектриса, висота трикутника?

2.Як обчислити периметр трикутника?

3.Де зосереджений центр маси трикутника?
8. Домашнє завдання.
Опрацювати §2 п.7  , №.134,№138,№141.

Давньогрецький математик,

фізик,інженер, винахідник

та астроном Архімед