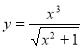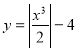Урок "Монотонність, парність і непарність функції.Неперервність функції".

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тема  уроку:  Монотонність, парність і непарність функції.

                         Неперервність функції.

 

Мета  уроку: Ознайомити учнів з поняттям зростання (спадання) функції, розуміти проміжки монотонності, користуючись графіком. Навчити досліджувати функцію на парність та монотонність і неперервність на заданому відрізку. Розвивати просторову уяву, логічне мислення, виховувати акуратність та зосередженість при виконанні досліджень та побудові графіків.

 

Тип уроку:   Комбінований

 

 

Х і д    у р о к у

І.  Організаційний момент.

     Повідомляю тему, мету уроку

 

ІІ. Актуалізація опорних знань. Перевірка д/з

 

  Функція  та  її  властивості

1. Дати означення функції

  Функцією  називається залежність  змінної  у  від  змінної  х,  якщо кожному значенню х відповідає  єдине  значення  у.

2. Як позначається функція, її складові?

  Позначення:  , де х – незалежна  змінна (аргумент);  у – залежна  змінна (функція) .

 3. Область визначення та множина значень функції

 Множина значень, яких набуває змінна  х називається

      областю визначення функції.      Позначення 

№	Функція	Область  визначення
1	(Многочлен  n-го степеня)
2	(дріб)
3
4

 

4. Множина  значень  залежної  змінної  у, яких  вона набуває при всіх значеннях х  називається  областю значень функції. Позначення:

 

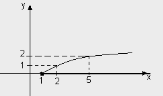
а) Яка область визначення функцій, графіки яких зображено на рис. ?

  область визначення функції  - це проміжок

, тому, що вираз       має  зміст при 

  ,   тобто  .

 

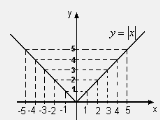
      область визначення функції  - вся  координатна

пряма       .      

б) Яка область значень функцій, графіки яких зображено на рис. ?

                   Область значень функції

                  множина  ;

 

             Область значень функції

                  множина .

 

 

 

ІІІ.  Сприйняття і усвідомлення нового матеріалу

 

 

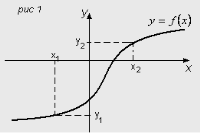
    Зростання, спадання, парність  та  непарність  функції.

 

• Якщо  для  будь-яких  двох  значень аргументу 

    більшому значенню аргументу  відповідає більше

   значення функції, то таку функцію називають зростаючою.

   ( ).  Рис 1.

 

 

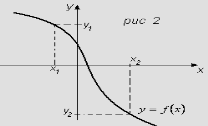
• Якщо  для  будь-яких  двох  значень аргументу 

    більшому значенню аргументу  відповідає менше

   значення функції, то таку функцію називають спадною.

   ( ).  Рис 2

 

 

 

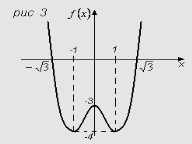• Функція  називається  парною, якщо для  будь-яких

     двох протилежних значень аргументу отримуємо  рівні 

     значення  функції, тобто . Графік парної

    функції симетричний відносно осі  Оу.

 

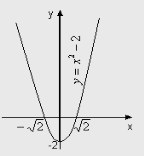
 Приклад. Функція є парною:

 . Рис 3  

 

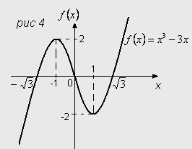• Функція  називається  непарною, якщо для  будь-яких

     двох протилежних значень аргументу отримуємо  протилежні 

     значення  функції, тобто . Графік непарної

    функції симетричний відносно початку координат.

 

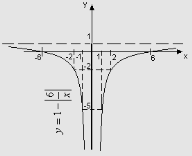
Приклад. Функція є непарною:

 . Рис 4

 

 

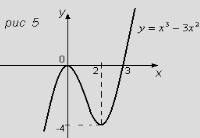
•        Велика кількість функцій не належить ні до парних ні до

                                                 непарних. Прикладом такої функції є функція

                                                  Рис 5.

 

 

 

 

 

ІV.  Вироблення  умінь  і  навичок

 

1.  Вказати область визначення та область значень, проміжки монотонності, дослідити на парність функції задані графіками

 

              

 

     

 

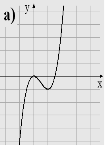
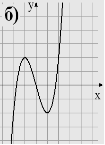
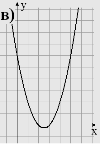
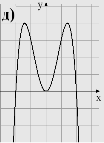
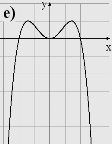
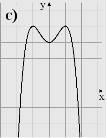
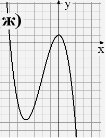
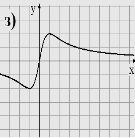
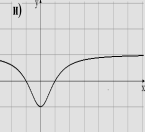
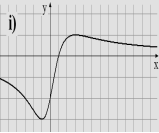
2.  В и к о н а н н я   в п р а в

1. Знайти область визначення  функцій:

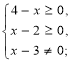
  Приклад: .   Р о з в 'я з а н н я. Арифметичний корінь існує лише для невід'ємних чисел, дріб існує при .  Маємо    

 

 Відповідь: .

 

а)	в)	д)
б)	г)  .	е)

 

2. Дослідити  на  парність і непарність  функції:        

а)

б)

в)

г)

 

3. Побудувати  графіки  функцій:

а)

б)

в)

г)

 

V.  Підсумок  уроку

       На цьому уроці ми навчились визначати область визначення функції та область значення функції, виконувати дослідження функцій на монотонність та парність, вивчили послідовність даних досліджень, перевіряти правильність виконання завдань за допомогою графічної інтерпретації, будуючи графіки функцій на комп’ютері

  VІ.  Домашнє  завдання

 

Знайти область визначення  функцій
Дослідити  на  парність і непарність  функції
Побудувати  графіки  функцій