Урок на тему "Дії над векторами, що задані координатами"
Тема уроку: Дії над векторами, що задані координатами.
Мета уроку:
Навчальна: навчити знаходити координати вектора, його абсолютну величину; домогтися засвоєння властивостей дій над векторами, вдосконалити вміння виконувати дії над векторами, що задані координатами.
Розвивальна: розвивати вміння практично реалізувати систему знань в систему вмінь; розвивати логічне мислення , творчі здібності учнів.
Виховна: виховувати культуру мови, дисциплінованість, увагу , інтерес до знань, прагнення їх здобувати.
Тип уроку: засвоєння нових знань та вмінь.
Наочність та обладнання: презентація, індивідуальні картки; картки – завдання для самостійної роботи.
Очікувані результати: учні виконують операції над векторами; знають визначення суми, різниці та добутку векторів; вміють виконувати дії над векторами, що задані координатами; можуть застосовувати властивість для доведення колінеарності двох векторів, чи перпендикулярності векторів.
Хід уроку
- Організаційний момент уроку.
Епіграф нашого уроку: « Тисячі шляхів ведуть до помилки,
але лише один – до істини.»
Жан-Жак Руссо
- Перевірка домашнього завдання
Перевірити якість виконаних домашніх завдань, зібравши зошити в кінці уроку у зазначених учнів. (вибірково)
- Актуалізація опорних знань . Робота з випереджувальним домашнім завданням: повторити тему «Вектори на площині». Вправа «Мікрофон».
Вчитель задає перше питання і передає уявний мікрофон учню, той відповідає, передає мікрофон іншому і задає наступне питання. Питання у кожного на парті.
- Що таке вектор? Як позначається вектор?
- Що таке довжина або модуль вектора?
- Які вектори рівні?
- Як знайти довжину вектора, якщо відомі його координати?
- Що називають різницею двох векторів?
- Що називається добутком вектора на число?
- Як додати вектори, коли відомо їх координати?
- Які координати мають рівні вектори? Колінеарні вектори?
- Як помножити вектор на число?
- Формулювання теми, мети і завдань уроку
Діти, ми продовжуємо вивчення нового розділу курсу геометрії 10 класу «Вектори у просторі». Ми з вами уже вивчили тему «Координати у просторі». Яку різницю ви помітили при вивченні цієї теми від координат на площині?
Отже сформулюємо основні задачі сьогоднішнього уроку.
- пригадати поняття вектора на площині,
- навчитися знаходити координати та абсолютну величину вектора у просторі,
- навчитися виконувати найпростіші дії з векторами (додавання, віднімання, множення на число тощо).
- Формування знань.
Перед вивченням нової теми нам необхідно згадати поняття вектора , координати вектора, абсолютну величину вектора, дії над векторами, ознаку колінеарності векторів, рівності векторів. Для цього давайте заповнимо таку таблицю. (таблиця підготовлена на ватмані і прикріплена на дошці).
Отже сформулюйте основні поняття в координатній формі, пов’язані з векторами у просторі. (учні по черзі заповнюють таблицю)
|
Вектори у просторі |
|
|
Для запису формул використовуємо |
А(х1;у1;z1), В(х1;у1;z1), |
|
напрямлений відрізок |
|
|
|
або |
|
якщо вони співнапрямлені і маютьрівні
довжини |
|
|
|
|
|
|
- Засвоєння знань. Сприймання і усвідомлення нового матеріалу.
Виконання письмових завдань «Зрозумів сам – поясни товаришу»
Завдання.
А) Дано точки А(3;4;5), В(2;2;2). Які координати векторів ![]() ;
; ![]() ?
?
Б) Які координати вектора ![]() , якщо А(6;2;-5), точка О – початок координат?
, якщо А(6;2;-5), точка О – початок координат?
В) Коли вектор ![]() відклали від початку координат, то дістали вектор
відклали від початку координат, то дістали вектор ![]() . Які координати точки А?
. Які координати точки А?
Г) Знайти ![]() , якщо А(3;7;9), В(5;4;3).
, якщо А(3;7;9), В(5;4;3).
Д) Дано точки А(2;-3;6), В(-3;5;4), С(-5;-2;-8), D(x;y;z). Знайдіть x;y;z, якщо ![]() .
.
Е) Абсолютна величина вектора ![]() дорівнює 7. Знайдіть z.
дорівнює 7. Знайдіть z.
Є) дано вектори ![]() . знайдіть
. знайдіть ![]() .
.
- Осмислення і усвідомлення вивченого матеріалу.
Вправа: «Векторні змагання» (біля дошки одночасно працюють три учні), інші працюють одночасно.
Завдання за підручником: №№ 1333(а,б,в)
Після виконання кожного – перевірка.
- Удосконалення вмінь і навичок. Самостійна робота
І рівень (2 бали)
-
Координати вектора
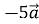 , якщо
, якщо 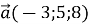 дорівнюють…
дорівнюють…
А) (9;3;24) Б) (9;-15;-24) В) (15;-25;-40) Г) (-9;5;8)
-
Який вектор дорівнює сумі векторів
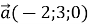 і
і 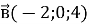 ?
?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]()
ІІ рівень (4 бали)
-
Якщо А(-3;6;2), В(2;-5;5), то координати вектора
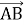 …
…
![]() , Б)
, Б) ![]() , В)
, В) ![]() , Г)
, Г) ![]() ,
,
-
Знайдіть довжину вектора
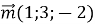 ?
?
А)![]() Б)
Б) ![]() В) 14 Г)
В) 14 Г) ![]()
ІІІ рівень (6 балів)
-
Дано вектори
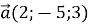 і
і 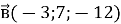 . Знайти абсолютну величину вектора
. Знайти абсолютну величину вектора 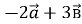 .
.
Відповіді: 1б; 2в; 3в; 4а; 5) ![]()
- Узагальнення отриманих знань. Повторимо питання , вивчені на уроці. Виконаємо вправу «Заповніть пропуски»
- Вектор – це………
- Щоб задати вектор , необхідні …….точки.
- Перша точка – це ……..вектора, а друга - ………. вектора.
- Якщо початок і кінець вектора збігаються, то вектор називається …….
- Щоб знайти координати вектора, треба від координати ……..вектора……. координату ……….вектора.
- Якщо у двох векторів……… координати рівні, то вектори називаються……..
- Довжиною вектора є ………між його початком і кінцем.
- За напрямком вектори бувають…………. і ……………., разом - …………..
- Якщо вектори колінеарні, то їх………….координати ……………………..
- Домашнє завдання.Опрацюватипараграф 36 . повторити правило трикутника і правило паралелограма. Виконати №№ 1319(а),1322,1334, 1338(а)
- Підсумки уроку. Оцінювання.
Підсумок уроку за схемою:
Важливо знати: формулу для обчислення довжини вектора; що є сумою, різницею та добутком векторів.
Важливо вміти: оперувати векторами, тобто виконувати дії над координатами даних векторів.
Зауважте: на запис виконання дій над координатами векторів.
Під час всього уроку належно працювали: ……..
Особливої похвали заслуговують такі учні: ………
Оцінювання (не менше 3-х оцінок)
- Рефлексія (осмислення результатів уроку). Вправа «Східці успіху»


про публікацію авторської розробки
Додати розробку
