Перпендикуляр і похила

  «Перпендикуляр і похила»

 Мета уроку:

• Сформувати поняття похилої; проекції похилої на площину; відстань від точки до площини; установити взаємозв’язок між довжинами похилих, проведених з однієї точки до площини, і довжинами їхніх проекцій на площину; формувати вміння застосовувати здобуті знання для розв’язування задач.
• Розвивати просторову уяву та  логічне мислення учнів.
• Виховувати розуміння ролі математики в житті, уважність, спостережливість. 
•  Тип уроку: урок засвоєння нових знань

 І. Організаційний момент уроку

 Хвилина мовчання, перевірка готовності до уроку.

ІІ. Перевірка домашнього завдання

1. Перевірити наявність виконаних завдань та відповісти на запитання, які виникли в учнів під час їх виконання.

  Опитування

1. Сформулюйте означення перпендикулярних прямих.

2. Дайте   означення   прямої,  перпендикулярної   до площини.

3. Сформулюйте   ознаку    перпендикулярності   прямої  та площини.

4. Скільки     прямих,    перпендикулярних    до      даної площини,     можна     провести    через    дану   точку?

ІІІ. Актуалізація опорних знань

    Щоб перейти до вивчення нової теми, ми повторимо теоретичний матеріал, який нам буде потрібний при вивченні нової теми .

Сформулюйте теорему Піфагора.

Як знайти невідомий катет за відомим катетом і гіпотенузою?

 IV. Формулювання теми, мети й завдань уроку.
Мотивація навчальної діяльності.

  Сьогодні ми повторимо властивості перпендикуляра і вивчимо, що таке похила і ії проекція.

Властивості перпендикуляра і похилої  застосовуються   на практиці.   Наприклад,   якщо встановлюють    щоглу (антену на радіостанції або на вітрильнику),  то стяжки беруть рівної довжини. Нижні кінці їх закріпляють   на    однакових відстанях  від  основи  щогли (рівномірно по колу). Це сприяє стійкості щогли.

V. Формування знань.

Перпендикуляр і похила до площини

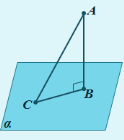Перпендикуляром,  проведеним  з даної  точки    до   даної   площини, називається відрізок,   що сполучає дану   точку    з    точкою   площини   і    лежить    на     прямій, перпендикулярній до площини.

 АВ – перпендикуляр

 Точка В – основа    перпендикуляра

Відстанню від даної  точки  до площини називається довжина  перпендикуляра,  проведеного з даної точки до даної площини.

 Похилою, проведеною з даної точки до даної площини, називається будь-який  відрізок,  який  сполучає  дану точку   з   точкою   площини   і   не   є перпендикуляром   до   площини.

 АС - похила

Точка С – основа похилої

Відрізок, який сполучає основи перпендикуляра та похилої,  проведених з однієї і тієї самої точки, називають проекцією похилої ВС – проекція похилої

         Властивості перпендикуляра й похилої

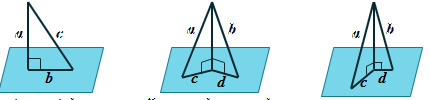
Якщо з точки, взятої поза площиною, проведено до

 площини перпендикуляр і похилі, то:

1.      перпендикуляр коротший за будь-яку похилу;
2.      проекції рівних похилих є рівними й, навпаки, похилі, що мають рівні проекції, є рівними;
3.     з двох похилих більша та, проекція якої більша.

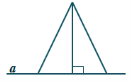
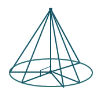
4)На відміну  від  площини, де  з  даної    точки   до   прямої можна   провести   тільки дві рівні   похилі,   у  просторі   з точки   до площини   можна провести         нескінченну множину   рівних    похилих, основи    яких     утворюють коло.

Теорема про три перпендикуляри

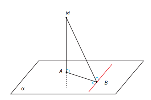Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна і до похилої.

VІ. Формування вмінь і відпрацьовування навичок

- усні вправи 35.7; 35.11

- письмові   вправи з підручнику № 35.3; 35.5;

VІІ. Підведення підсумків уроку. Рефлексія

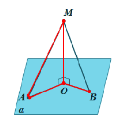З точки М, що не належить площині, проведені дві похилі МВ і МА та перпендикуляр МО.

 1. Назвіть відрізок, довжина якого дорівнює відстані від точки М до площини α?

 2. Якщо МА = 9 см, МВ = 12 см, то яка    проекція   буде більша?

 3. Якщо АО = 3 см, ОВ = 1 см, то яка похила більша?

 4. Якщо МА : МВ = 5 : 6, то яка  проекція    буде   менша?

VІІІ. Домашнє завдання

 Опрацювати п. 35 ст. 185-189.

                       Вправи 34.10; 35.4; 35.6