Урок на тему "Елементарні геометричні фігури та їх властивості"

Урок № 54                                                                                     Дата    05.05.2020р.

Я рада вас привітати, любі мої учні!

Все ближче кінець навчального року і ми з вами повині гідно його закінчити. Наберіться ще трохи сил, та згадайте матеріал, який ви вже вивчили.

Натхнення вам та доброго здоров´я, бережіть себе!

Тож, до роботи, шановні мої семикласники!

Нагадую!

• Все, що прописано курсивом, повино обов´язково бути записано у вашому  зошиті;
• Ті учні, які не можуть працювати разом з нами та виконувати запропановані домашні роботи (з різних причин), будь ласка, кожного уроку відкривайте “ Робочий зошит” або підручник та переписуйте повністю всі правила і приклади (згідно теми уроку) із рубрики “Розв´язуємо разом”. За сумлінне виконання отримаєте - 5 балів.

Відкрийте зошит і записуйте:

П´яте травня

Класна робота

Тема уроку   Повторення і систематизація навчального матеріалу. Елементарні

                       геометричні фігури та їх властивості.

Мета уроку: удосконалити знання означеннь  елементарних геометричних фігур; удосконалити вміння застосовувати це означення та властивості до розв’язування задач; розвивати вміння виділяти головне в досліджуваному матеріалі; вибирати  і використовувати необхідну інформацію для розв’язування  задач; виховувати впевненість у власних силах, принциповість та старанність.

Тип уроку: удосконалення знань, умінь та навичок

Хід уроку

І. Організаційний етап

Підготуйте необхідні інструменти для креслення , зошит і починаємо згадувати попередній матеріал.

IІ. Актуалізація опорних знань

1. Що означає слово «геометрія»?
2. Що вивчає геометрія?
3. Що таке планіметрія?
4. Як позначаються точки?
5. Як позначаються прямі?

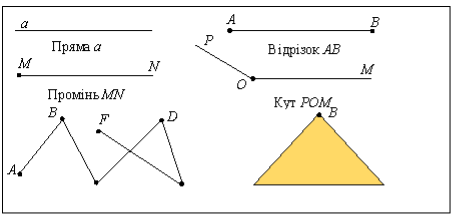
Перегляньте, будь ласка, таблиці та запишить у зошит головне:

Завдання 1. Точка Р не належить прямій MN. Точка К – середина відрізка PN, точка Q – середина відрізка NM. Як розміщені прямі MN і QК?

Розв’язання:

Відповідь: В

Завдання 2. Точка Р належить відрізку CD. Чому дорівнює відстань СР, якщо CD = 78 см, DP = 24 см?

Розв’язання:

СР = CD – DP;

СР = 78 – 24 = 54 (см).

Відповідь: В

Завдання 3. Точка А – середина відрізка КР, точка В – середина відрізка АР. Знайдіть довжину відрізка КВ, якщо ВР = 12 см.

Розв’язання:

АР = 2 АВ, оскільки точка В середина відрізка АР.

АР = 2 · 12 = 24 (см);

КР = 2 АР, оскільки точка А середина відрізка КР.

АР = 2 · 24 = 48 (см);

КВ = КР – ВР;

КВ = 48 – 12 = 36 (см).

Відповідь: Б

Завдання 4. Промінь РК проходить між сторонами кута МРN. Яка з наведених рівностей неправильна?

Відповідь: Г

Завдання 5. Промінь ОК проходить між сторонами кута АОВ. Встановіть відповідність між видом кута (1 – 4) та його градусною мірою (А – Г).

Відповідь: 1 – Г; 2 – В; 3 – Б; 4 – А.

Завдання 6. Промінь СМ – бісектриса кута АСВ. Чому дорівнює кут ВСА,

                     якщо МСВ = 34º?

Відповідь: А

Завдання 7. Точка Р належить відрізку MN. Чому дорівнює відстань між точкою Р і серединою відрізка MN, якщо МР = 18 см, NP = 6 см?

Розв’язання:

Точка К – середина відрізка MN.

Точка Р – належить відрізку MN.

MN = МР + NP;

За умовою задачі, МР = 18 см, NP = 6 см, тоді MN = 18 + 6 = 24 (см).

Оскільки точка К – середина відрізка MN, то МК = KN = MN.

МК = KN = · 24 = 12 (см);

КР = MN – NP – МК;

КР = 24 – 6 – 12 = 6 (см).

Відповідь: 6 см.

Завдання 8. Промінь ділить розгорнутий кут на два кути, один з яких на 30º більший за другий. Знайдіть утворені кути.

Розв’язання:

АСВ – розгорнутий, АСВ = 180º.

Нехай РСВ = х, АСР = х + 30º.

За умовою задачі, АСВ = 180º і АСВ = АСР + РСВ, тоді складемо і розв’яжемо рівняння:  х + х + 30º = 180º;

                                      2х + 30º = 180º;

                                      2х = 180º – 30º;

                                      2х = 150º;

                                      х = 150º : 2;

                                      х = 75º.

Отже,  РСВ = 75º, АСР = 75º + 30º = 105º.

Відповідь: 75º; 105º.

Завдання 9. Прямий кут поділено на три кути, градусні міри яких відносяться

                      як 4 : 1 : 4. Знайдіть величини цих кутів.

Розв’язання:

Нехай х – коефіцієнт пропорційності, тоді величина першого кута становить 4хº, другого – хº, а третього – 4хº. За умовою задачі, градусна міра прямого кута становить 90º, тоді складемо і розв’яжемо рівняння:

4х + х + 4х = 90;

9х = 90;

х = 90 : 9;

х = 10.,

Отже, градусна міра першого кута становить 4 · 10 = 40º, другого – 10º, а третього – 4 · 10 = 40º.

Відповідь: 40º; 10º; 40º. 

V. Підсумки уроку

Дидактична гра «Вірю – не вірю»

Чи правильне твердження?

Запитання 1. Геометрія – це наука про геометричні фігури та їх властивості.

Запитання 2. У перекладі з грецького слово «геометрія» означає землемірство.

Запитання 3. Розділ геометрії, у якому вивчають фігури на площині, називають планіметрією.

Запитання 4. Наука геометрія виникла на початку ХХІ століття.

Запитання 5. Промінь і відрізок – це різні назви однієї і тієї самої фігури.

Запитання 6. Пряма не має довжини.

Запитання 7. Геометричні фігури позначаються латинськими буквами.

Запитання 8. Не існує кута величиною 1º.

Запитання 9. Усі сторони квадрата рівні.

Запитання 10. У трикутнику не може бути тупого кута.

Запитання 11. Кут, величина якого дорівнює 90º, називають кривим.

Запитання 12. Коло і круг – це різні геометричні фігури.

Я сподіюсь, що сьогодні, працюючи дистанційно разом, ви з радістю та  впевнено йшли до успіху. Дякую за урок!

Від класної роботи пропустили чотири клітинки вниз і записуємо:

                                            П´яте  травня

Домашня  робота

VІІ. Домашнє завдання

• Повторити: § 1, пункт 1 – 3;
• Завдання 1. Точка D не належить прямій AO. Точка C – середина відрізка

                AD, точка O – середина відрізка AB. Як розміщені прямі CВ і AD?

Завдання 2.

Точка Т належить відрізку КР. Чому дорівнює відстань РТ, якщо КР = 48 см, КТ = 16 см?

Завдання 3. Точка Р – середина відрізка МК, точка К – середина відрізка MN.  

                      Знайдіть довжину відрізка МР, якщо КN = 18 см.

Відправити на Google – диск  відповіді гри «Вірю – не вірю» та домашню роботу.