Урок "Зовнішній кут трикутника 7 клас"

Геометрія, 7 клас

 

Тема. Зовнішній кут трикутника.

Мета уроку: забезпечити розуміння вивчення поняття «зовнішній кут трикутника»,засвоєння властивостей зовнішнього кута трикутника;

формувати логічні вміння при доведенні теореми, вміння творчої діяльності учнів самостійно застосовувати знання до розв’язування задач;

виховувати почуття краси естетикою фракталів, формувати правильні уявлення, пов’язані з умовами і причинами, що викликали виникнення фракталів, які дали поштовх розвитку різних галузей математики.

Тип уроку: комбінований.

Обладнання: мультимедійна дошка, диск з презентацією, косинець або лінійка.

 

Хід уроку

(Слайд №1)

Слово учителя.   У великому саду геометрії

кожний може підібрати собі букет за смаком

                                              Д. Гільберт

 

На сьогоднішньому уроці кожний з вас буде складати свій букет.

Ви будете розв’язувати задачі, доводити теорему, познайомитесь з новим поняттям. Геометрія - це не тільки теореми та задачі, це і архітектура, мистецтво. Ми ще раз переконаємось, що геометрія «красива наука».

I. Актуалізація опорних знань, навичок і умінь.

 Учням роздаються карточки для усного рахунку із задачами з тем «Сума кутів трикутника» та «Суміжні кути». На мультимедійній дошці записані відповіді. Якщо усі учні правильно розв’язують приклади, то на мультимедійній дошці відкривається картинка із фракталом. Керівник групи робить невелике повідомлення про фрактали. ( Керівники груп одержали випереджаюче домашнє завдання з даної теми.)  Першими починають працювати учні 1 групи .

 

Робота у групах.

1 група.

(Слайд 2)

Знайти невідомий кут  трикутника, якщо два кути його дорівнюють:

  1) 55⁰ і 70⁰;

Розв’язування:

55⁰  + 70⁰ = 125⁰

180⁰  - 125⁰ = 55⁰  

Відповідь: 55⁰

2) 53⁰ і 47⁰

Розв’язування:

53⁰  + 47⁰ = 100⁰

180⁰  - 100⁰ = 80⁰  

Відповідь: 80⁰

  3) 20⁰ і 69⁰

Розв’язування:

20⁰  + 69⁰ = 89⁰

180⁰  - 89⁰ = 91⁰  

Відповідь: 91⁰

4) 41⁰ і 39⁰

Розв’язування:

 41⁰  + 39⁰ = 80⁰

180⁰  - 80⁰ = 100⁰  

Відповідь: 100⁰

 

 Керівник 1 групи.  Фрактал -  геометрична фігура, певна частина якої повторюється знову і знову, змінюючись в розмірах. Звідси випливає принцип самоподібності. Всі фрактали подібні самим собі, тобто вони схожі на всіх рівнях.
    2 група.

(Слайд 3)

Знайти  гострий кут прямокутного трикутника, якщо інший  дорівнює:

1) 55⁰; 

Розв’язування:

 90⁰  - 55⁰ = 35⁰

Відповідь:  35⁰

 2) 53⁰;

Розв’язування:

 90⁰  - 53⁰ = 37⁰

Відповідь:  37⁰

 3) 21⁰;

Розв’язування:

 90⁰  - 21⁰ = 69⁰

Відповідь:  69⁰

 4) 57⁰

Розв’язування:

 90⁰  - 57⁰ = 33⁰

Відповідь:  33⁰

 

Керівник 2 групи.  Приблизні фрактали можна легко знайти в природі. Як приклади можна назвати хмари, сніжинки, гори, мережі річок.
Подивіться на дерево, потім виберіть певну гілку і вивчіть її ближче. Тепер виберіть зв’язок з декількох листів. Для вчених, що займаються фракталами, всі ці три об’єкти представляються ідентичними.

3 група.      

 (Слайд 4)

Якого виду трикутник, якщо два кути його дорівнюють:

  1) 21⁰ і 49⁰;

Розв’язування:

180⁰ – ( 21⁰  + 53⁰ ) = 106⁰

Відповідь: тупокутний .

   2) 60⁰ і 60⁰;

Розв’язування:

180⁰ – ( 60⁰  + 60⁰ ) = 60⁰

Відповідь:  рівносторонній  .

 3) 55⁰ і 70⁰;

Розв’язування:

180⁰ – ( 55⁰  + 70⁰ ) = 55⁰

Відповідь:  гострокутний.

 4) 30⁰ і 60⁰.

Розв’язування:

180⁰ – ( 30⁰  + 60⁰ ) = 90⁰

Відповідь:  прямокутний.

Керівник 3 групи. Фрактали завжди асоціюються зі словом  хаос. Фрактали проявляють хаотичну поведінку, завдяки якій вони здаються такими безладними і випадковими. Але якщо поглянути досить близько, можна побачити багато аспектів самоподібності всередині фрактала.

 

4 група.

(Слайд 5)

Знайдіть кут суміжний з кутом:

1) 35⁰;

Розв’язування:

180⁰ –  35⁰  = 145⁰

Відповідь:  145⁰

 2) 108⁰;

Розв’язування:

180⁰ –  108⁰  = 72⁰

Відповідь:  72⁰

 3) 29⁰;

Розв’язування:

180⁰ –  29⁰  = 151⁰

Відповідь:  151⁰

 4) 138⁰.

Розв’язування:

180⁰ –  138⁰  = 42⁰

Відповідь:  42⁰   .

Керівник 4 групи.  Для багатьох вчених, вивчення хаосу і фракталів не просто нова область пізнання, яка об’єднує математику, теоретичну фізику, мистецтво та комп’ютерні технології – це революція.  Це відкриття нового типу геометрії, тієї геометрії, яка описує світ навколо нас і яку можна побачити не тільки в підручниках, а й у природі і скрізь в безмежній всесвіту.

ІІ.  Перевірка домашнього завдання

Слово вчителя. Ви познайомились із новим геометричними фігурами які називаються фракталами і розв’язували задачі, аналогічні до тих, які ви виконували вдома (фронтальна перевірка домашнього завдання).

Які теореми ми використовували при розв’язуванні задач?

(Відповіді учнів супроводжуються показами слайдів).

  Теорема про суму кутів у трикутнику.

( Слайд 6)

 Теорема про суміжні кути.

( Слайд 7)

ІІ. Мотивація навчальної діяльності.

Слово вчителя. Побудуємо довільний трикутник і продовжимо його сторони. Які кути утворилася ? Чому дорівнює їх сума?

Для того, щоб відповісти на ці запитання ми сьогодні будемо вивчати нову тему, яка називається “Зовнішній кут трикутника ”.

 

ІІІ.  Пояснення нового матеріалу.

 ( Слайд 8)

Слово вчителя. При побудові малюнка ми дістали кут суміжний з кутом трикутника. Такий кут називається зовнішнім кутом. Назвіть всі зовнішні кути, які ви бачите на екрані. 

Теорема (властивість зовнішнього кута трикутника).

Зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів не суміжних з ним.

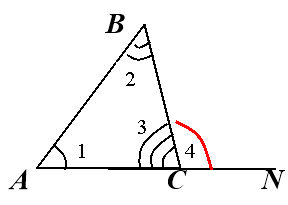Дано: ,    або  – зовнішній кут       трикутника АВС.                                                            Довести:    .  

Доведення:

-  як сума  кутів  трикутника.        -  як сума суміжних кутів.

                 Отже, .

     Теорему доведено.

2. Мозковий штурм.

 ( Слайд 9)

1. Назвіть внутрішні кути не суміжні з зовнішнім кутом ВСN.

2. Який кут є суміжним до кута ВСN ?

3. Чому дорівнює сума кутів у трикутнику ?

4. Чому дорівнює сума суміжних кутів ?

5.  Чому дорівнює ?

6. Яким буде зовнішній кут трикутника, порівняно з внутрішнім кутом, не суміжним з ним ?

ІV. Засвоєння вивченого матеріалу.

1.  Робота з підручником по групах.

1 група Знайдіть зовнішній кут трикутника АВС при вершині даного кута, якщо   .

Розв’язування:  180⁰ - 57⁰ = 123⁰

Відповідь:  123⁰

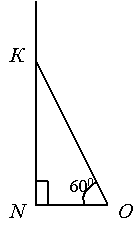
2 група За даними наведеними на малюнку, знайдіть зовнішній кут при вершині К трикутника   КОN.

 Розв’язування:  90⁰  + 60⁰ = 150⁰

Відповідь: 150⁰

 

 

 

 

 

 

 

 

 

 

 

 

3 група Скільки зовнішніх кутів у трикутника? 

Відповідь: три

4 група  Знайдіть зовнішній кут трикутника АВС при вершині даного кута, якщо   .

Розв’язування:  180⁰  - 34⁰ = 146⁰

Відповідь:  146⁰

2.  Розв’язування задач на слайдах

( Слайд 10)

Роз’язування:

1) 180⁰  - 140⁰ = 40⁰

2) 180⁰  - 70⁰ = 110⁰

3) 110⁰  + 40⁰ = 150⁰

4) 180⁰  - 150⁰ = 30⁰

Відповідь:  30⁰

( Слайд 11).

 

Роз’язування:

1) 180⁰  - 120⁰ = 60⁰

2) 50⁰ + 60⁰ = 110⁰

3) 180⁰  - 110⁰ = 70⁰

Відповідь:  70⁰

3.  Самостійна робота по групах. Учні виконують малюнки і роблять скорчений запис розв’язування задач. Один учень з кожної групи розв’язує задачу біля дошки. 

1 група. Зовнішній кут трикутника дорівнює 100⁰, Знайдіть кути трикутника, якщо один із них дорівнює 40⁰.

Роз’язування:

1) 180⁰  - 100⁰ = 80⁰

2) 100⁰ - 40⁰ = 60⁰

Відповідь:  80⁰  і 60⁰

2 група. Зовнішній кут трикутника дорівнює 100⁰, Знайдіть кути трикутника, якщо один із них дорівнює 55⁰.

Роз’язування:

1) 180⁰  - 100⁰ = 80⁰

2) 100⁰ - 55⁰ = 45⁰

Відповідь:  80⁰  і  45⁰

3 група. Знайдіть гострі кути прямокутного  трикутника, якщо його зовнішній кут дорівнює 120⁰.

Роз’язування:

1) 180⁰  - 120⁰ = 60⁰

2) 90⁰ - 60⁰ = 30⁰

Відповідь:  60⁰  і  30⁰

4 група.  Знайдіть гострі кути прямокутного  трикутника, якщо його зовнішній кут дорівнює 132⁰.

Роз’язування:

1) 180⁰  - 132⁰ = 48⁰

2) 90⁰ - 48⁰ = 42⁰

Відповідь:  48⁰  і  42⁰

V. Формування навичок практичного використання.

Задача на фракталі

( Слайд 12).

Дано  трикутник АВС у фракталі. Зовнішній кут трикутника дорівнює 120⁰. Знайдіть кути трикутника не суміжні з ним, якщо вони пропорційні числам 3 і 5.

Роз’язування:

Нехай х градусна міра, що припадає на одну частину кута, тоді

3х + 5х = 120⁰

8х = 120⁰

 х = 120^{0 :} 8

х = 15⁰

 15⁰ * 5 = 75⁰

15⁰ * 3 = 45⁰

Відповідь:  45⁰  і  75⁰

(Учням пропонується скласти свої задачі, використовуючи даний малюнок).

VІ. Підсумок уроку.

Кросворд

( Слайд 13).

 

		3
		Г
		О					8	9
		С				7	Ч	Ф
	2	Т		5		Л	О	Р
1	П	Р	4	Т	6	І	Т	А
Т	Р	И	К	У	Т	Н	И	К
Р	Я	Й	У	П	Р	І	Р	Т
И	М		Т	О	И	Й	И	А
	О			К	Н	К		Л
	К			У	А	А
	У			Т	Д
	Т			Н	Ц
	Н			И	Я
	И			Й	Т
	Й				Ь

 

1. Скільки зовнішніх кутів у трикутнику?
2. Трикутник, у якого зовнішній кут дорівнює 90⁰.
3. Зовнішній кут трикутника – тупий. Яким є внутрішній кут, суміжний з ним?
4. Геометрична фігура, яка вимірюється в градусах.
5. Трикутник, у якого один з внутрішніх кутів більший за 90⁰.
6. Зовнішній кут трикутника дорівнює 167⁰_.  Знайти величину внутрішнього кута, суміжного з ним?
7. Креслярський інструмент.
8. Один із суміжних кутів дорівнює 176⁰. Скільки градусів становить інший кут?
9. Геометрична фігура, певна частина якої повторюється знову і знову, змінюючись в розмірах. 

 

VІІ. Домашнє завдання.