Урок на тему "Функції y = sinx та y = cosx, їх графіки та властивості"

Клас: 10

Урок № 10/3.

Профільний рівень

Тема. Функції та , їх графіки та властивості.

Мета.

Дидактична: удосконалювати вміння й навички будувати графіки тригонометричних функцій та , проводити дослідження тригонометричних функцій, формувати компоненти дослідницької компетентності.

Розвивальна: розвивати просторову уяву, логічне мислення, графічну культуру.

Виховна: виховувати культуру математичного мовлення та сумлінне ставлення до навчання.

Тип уроку: узагальнення та систематизації знань.

Обладнання: картки «Властивості функцій».

Підручник: Мерзляк А. Г. Алгебра і початки аналізу: підруч. для 10 кл. загальноосвіт. навч. закладів: проф. рівень / А. Г. Мерзляк,
Д. А. Номіровський, В. Б. Полонський, М. С. Якір. – Х.: Гімназія,
2010. – 416 с.

Структура уроку

1. Організаційний момент (3 хв).

2. Перевірка домашнього завдання (4 хв).

3. Актуалізація опорних знань та мотивація навчальної діяльності (6 хв).

4. Узагальнення та систематизація знань (27 хв).

5. Підсумки уроку та повідомлення домашнього завдання (5 хв).

Хід уроку

1. Організаційний момент (3 хв).

Привітання. Повідомлення теми та мети уроку.

2. Перевірка домашнього завдання (4 хв).

Учні обмінюються зошитами та здійснюють взаємоперевірку.

3. Актуалізація опорних знань та мотивація навчальної діяльності (6 хв).

Фронтальне опитування.

Учні відповідають на питання вчителя

1. Назвіть область визначення функції .

2. Назвіть область значень функції .

3. Чи періодична функція ?

4. Чи парна функція ?

5. Назвіть область визначення функції

6. Назвіть область значень функції .

7. Чи періодична функція ?

8. Чи парна функція ?

9. Які найбільші та найменші значення приймають функції та

?

Відповіді:

1. Область визначенняя – множина всіх дійсних чисел.

2. Область значень [-1; 1].

3. Так. Період .

4. Так. Функція парна.

5. Область визначенняя – множина всіх дійсних чисел.

6. Область значень [-1; 1].

7. Так. Період .

8. Ні. Функція непарна.

9. Функція  приймає:  найбільше значення, рівне 1, при
; найменше значення, рівне −1, при  .

Функція  приймає:  найбільше значення, рівне 1, при
; найменше значення, рівне −1, при  .

Вчитель пропонує до обговорення проблемне питання: «Що може пришвидшити процес дослідження функції»?

Учні приймають активну участь в обговоренні та висувають припущення: «графік функції дуже виразно її характеризує. На графіку функцій відразу видно як ті проміжкизростання та спадання функції, найбільші і найменші значення функції – як на всій області визначення, так і на окремих її проміжках. На графіку можна прослідкувати періодичність, симетричність функції».

4. Узагальнення та систематизація знань (27 хв).

Робота у групах. Учні об’єднуються в мікрогрупи та отримують наступні завдання (навчально-теоретичні задачі III рівня):

1. Запишіть алгоритм дослідження та побудуйте графік функції
.

2. Запишіть алгоритм дослідження та побудуйте графік функції
– 1.

Розв’язання.

Алгоритм дослідження функції

і побудови її графіка

1. Знайти період заданої функції. .

2. Описати, за допомогою яких перетворень на площині з графіка функції можна отримати графік функції .

2.1. Стиснемо графік функції до осі ординат в 2 рази, отримаємо графік функції .

2.2. Стиснемо графік функції в 2 рази до осі абсцис, отримаємо графік функції .

3. Записати проміжки зростання даної функції.

, .

4. Записати проміжки спадання даної функції.

, .

5. Указати найбільше та найменше значення функції.

Найбільше: , найменше:.

6. Побудувати графік функції.

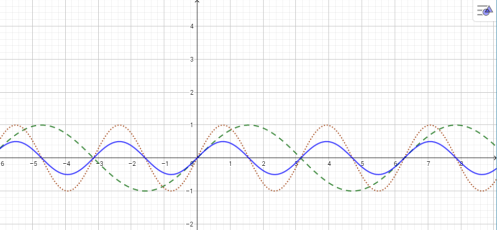
Рис. 2.9. Графік функції .

Алгоритм дослідження функції – 1

і побудови її графіка

1. Знайти період заданої функції. .

2. Описати, за допомогою яких перетворень на площині з графіка функції можна отримати графік функції .

2.1. Виконаємо паралельне перенесення вздовж осі абсцис графіка функції на одиниць у від’ємному напрямку, отримаємо графік функції

2.2. Симетрично відобразими графік функції відносно осі ординат, отримаємо графік функції .

2.3. Виконаємо паралельне перенесення вздовж осі ординат графіка функції на 1 одиницю у від’ємному напрямку, отримаємо графік функції .

3. Записати проміжки зростання даної функції.

4. Записати проміжки спадання даної функції.

5. Указати найбільше та найменше значення функції.

Найбільше:0, найменше:.

6. Побудувати графік функції.

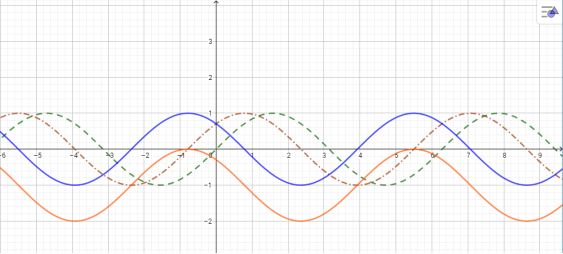
Рис. 2.10. Графік функції .

Робота за підручником. Учні виконують біля дошки та в зошитах номери: № 750, № 752.

№ 750. Серед чисел укажіть

1) нулі функції ;

2) значення аргументу, при яких функція набуває найбільшого значення;

3) значення аргументу, при яких функція набуває найменшого значення.

Відповідь:

1) ; 2) ; 3) .

№ 752. На яких з наведених проміжків функція є спадною ?

1) ; 2) ; 3) ; 4)

Відповідь: ;.

Вчитель роздає учням картки, які вони мають заповнити.

5. Підсумки уроку та повідомлення домашнього завдання (5 хв).

Вправа « «Так» чи «ні»» ?

1. Функція парна.

2.Область визначення функції проміжок .

3. Функція періодична з періодом 5π.

4. Функція періодична з періодом 2π.

5. Область значень функції : [-1; 1].

Відповіді:

1. Ні.

2. Ні.

3. Ні.

4. Так.

5. Так.

Домашнє завдання. §4 с. 244 - 248 (опрацювати), виконати №749, № 751.

№ 749.

Відповідь: 1); ; ; 0; ; 6; . 2) ; . 3) ; ; .

№ 751

Відповідь: ; .

Задачі, які пропонуються учням на уроці, сприяють розвитку різних компонент дослідницької компетентності, зокрема мотиваційно-ціннісного та когнітивного.