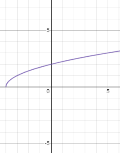
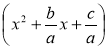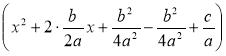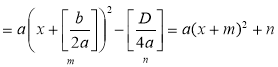Урок на тему:"Функція у = ax2 + bx + c, її властивості та графік."

Про матеріал

Метою даного уроку: формування знань учнів про означення, вид графіка та алгоритм побудови графіка квадратичної функції, сформувати первинні вміння розпізнавати квадратичну функцію серед інших елементарних функцій; навчитись знаходити координати вершини та напрям віток графіка квадратичної функції; виконувати побудову графіка квадратичної функції за ви-вченими алгоритмами та повторити загальні властивості функцій, а також схеми виконання основних видів геометричних перетворень графіків функцій.

Перегляд файлу

Клас : 9

УРОК 23

Тема уроку. Функція у = ax² + bx + c, її властивості та графік.

сформувати знання учнів про означення, вид графіка та алгоритм побудови графіка квадратичної функції;
сформувати первинні вміння розпізнавати квадратичну функцію серед інших елементарних функцій;
знаходити координати вершини та напрям віток графіка квадратичної функції;
виконувати побудову графіка квадратичної функції за вивченими алгоритмами;
повторити загальні властивості функцій, а також схеми виконання основних видів геометричних перетворень графіків функцій.

Мета уроку:

Тип уроку: формування знань, вироблення первинних умінь.

Наочність та обладнання: опорний конспект, роздавальний матеріал, презентація.

Хід уроку

І. Організаційний етап

Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.

II. Перевірка домашнього завдання . Актуалізація опорних знань

1. Опишіть перетворення, за допомогою якого з графіка y = f(x) можна побудувати графік функції g(x), якщо:

1) g(x) = -f(x);

2) g(x) = 2f(x);

3) g(x) = f(x - 2);

4) g(x) = f(x) – 2.

2. Установіть відповідність між функцією та її графіком.

А $C:\Users\админ\Downloads\saveaspng.png$

Б $C:\Users\админ\Downloads\saveaspng (7).png$

1. у=х²+3

2. у= -х²+3

3. у=

4. у=(х-2)²-4

5. у= - – 2

6. у=х-5.

В $C:\Users\админ\Downloads\saveaspng (6).png$

Г $C:\Users\админ\Downloads\saveaspng (3).png$

Ґ $C:\Users\админ\Downloads\saveaspng (4).png$

Д $C:\Users\админ\Downloads\saveaspng (5).png$

Відповідь: 1-А. 2- Ґ. 3-Д. 4-Г. 5-В. 6-Б.

3. Назвіть коефіцієнти квадратного тричлена:

1) 3х²– 5х + 2; 2) х² – 5х; 3) -х²– 2;

4) -х²; 5) х².

4. Розв'яжіть рівняння:

1) х² + х = 0; 2) х²+ 2x + 1 = 0;

3) x²– 3x + 2 = 0; 4) 2х² – 5х + 2 = 0.

Відповідь: 1) -1;0. 2) -1. 3)1; 2. 4) ; 2.

III. Формулювання мети і завдань уроку.

Мотивація навчальної діяльності учнів

Учень 1:

Між планетами, між породами,

Між рослинами, між народами

Випадково чи з необхідності –

Скрізь простежуються відповідності.

Поміж зграями і кошарами,

Між суспільствами і державами,

І в конструкціях, і в інструкціях -

Відповідності, тобто функції.

Від мікробини до безмежності

Скрізь залежності і залежності.

Від ціни на газ, на одежину

Ми залежимо, ще й як залежимо!

Там – від долара, там – від унції…

А залежності – також функції.

Учень 2: ( Історична довідка)

Функція – одне з найважливіших понять сучасної математики . Воно виникло в

ХVII ст. . Поняття змінної величини і функції вперше ввів Р. Декарт . Термін

функція походить від латинського слова funktio , що означає діяльність ,

виконання . Його ввів німецький математик Г. Лейбніц у 1694 році .

Учитель. Вивчивши способи геометричних перетворень графіків функцій, можна побудувати графік будь-якої алгебраїчної функції, рівняння якої утворене з найпростіших рівнянь функцій: y = kx; у = ; у =х²; у = х³; у = . Тому цілком логічно після вивчення способів перетворень графіків елементарних функцій вивчити питання про інші, крім названих, види функцій та їхні графіки. Однією з таких функцій є функція, графік якої можна утворити з графіка функції у = х² шляхом виконання одного або кількох геометричних перетворень, — квадратична функція. Це завдання і визначає основну дидактичну мету уроку.

IV. Формування знань

План вивчення нового матеріалу

Означення квадратичної функції.
Графік квадратичної функції.
Алгоритм побудови графіка функції y = ax² + bx + c.

Опорний конспект

*Функція виду у* = ax² + bx + c, де а *0, називається квадра**тичною.*
Наприклад: — квадратичні функції.
Графік квадратичної функції — парабола, вітки якої напрямлені вгору, якщо а > 0, і вниз — якщо а < 0 .
Координати вершини (х₀; у₀) параболи графіка у = ах² + bх + с обчислюються за формулами:
; або
Наприклад: у функції у = х²+ 2х – 3, яка є квадратичною, графік — парабола. Вітки параболи напрямлені вгору (а = 1 > 0), а координати вершини:
;
або y₀ = f (-1) = (-1)²+ 2 ∙ (-1) – 3 = 1 – 2 – 3 = -5 + 1 = -4.
Тобто вершина параболи (-1; - 4).

Побудова графіка функції у = ах² + bх + с, а 0.

Спосіб 1

Спосіб 2

1. Обчислити абсцису вершини

1. Виділити повний квадрат:

ах² + bх + с = а=

2. Підставити х₀ у рівняння і знайти у₀.

3. Побудувати параболу у = ах²з вершиною в точці (х₀; у₀). Якщо а > 0, вітки параболи напрямлені вгору, якщо а < 0 — вниз.

4. Для більшої точності побудови знайти точки перетину графіка з координатними осями.

= а= .

2. Використавши схему геометричних перетворень графіків функцій, виконати побудову параболи у = х², потім її розтягнення (або стиснення) до параболи у = ах², а потім виконати паралельне перенесення у = ах²вздовж осі Ох на – т і вздовж осі Оу на п.

Учитель : А яке ж практичне застосування квадратичної функції ? ( на слайді картинки с зображенням параболічних дзеркал , прожекторів , мостів , арок тощо.)

Інженерні розрахунки і практика засвідчують , що споруди та конструкції (ферми мостів, арки), обриси яких нагадують параболу або гіперболу , мають підвищену міцність. Властивості квадратичної функції враховують при виготовлені параболічних дзеркал, прожекторів, шаблонів для виробництва деталей тощо.

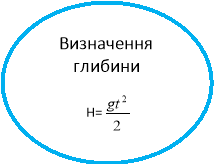
За допомогою квадратичної функції можна описати низку різноманітних процесів , явищ у природі , в побуті , на виробництві . На приклад , рух тіла , що вільно падає, описує функція виду y=4,9x² , яка дає , зокрема , можливість знайти відстань у ( в метрах ), яку пролетить тіло за x секунд.

Застосування квадратичної функції

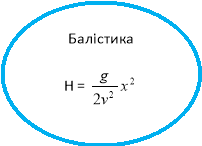
V. Формування первинних умінь

Усні вправи

Яка з наведених функцій є квадратичною:
1) у = х²; 2) у = х²+ 2; 3) у = -х²– 2х + 1; 4) у = х² – х + х³?
На рисунку зображено графік функції у = ах² + bх + с. Використавши подані на

рисунку умови, укажіть:

а) знак числа а в рівнянні у = ах²+bх + с;

б) координати вершини параболи;

в) вісь параболи.

3. Визначте координати точок перетину з осями Ох і Оу графіка функції:

1) у = х² – 2х + 1; (Відповідь (1;0), (0;1) )

2) у = х² – 3х + 2; (Відповідь (1;0), (2;0), (0;2) )

3) у = х² + х + 2. (Відповідь (0;2) )

Письмові вправи

1. Визначити значення функції у= x²+4x-5, якщо значення аргументи дорівнює -1; 3; 0.

Відповідь: f(-1)= -8; f(3)= 16; f(0)= -5.

2. Визначити напрямок віток параболи та координати вершини:

а) у = -х²+ 2х + 8; б) у = 2х²+ 6х + 7; в) у= 2х²+ х – 6.

Відповідь: а)(х₀;у₀)=(1;11); б) )(х₀;у₀)=(1,5;20,5); в) )(х₀;у₀)=(- ;-6).

3. Побудувати графік функції:

а) у =2х²+ 8х + 4;

б) у = -х²+ 4х – 3.

в) у =2х²- х + 3.

Відповідь:

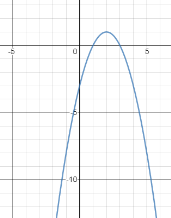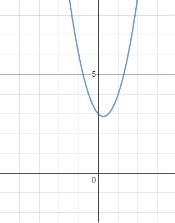
а) б) $C:\Users\админ\Downloads\saveaspng (19).png$ в) $C:\Users\админ\Downloads\saveaspng (20).png$

VII. Підсумки уроку

Контрольні запитання

Опишіть, що являє собою графік функції:
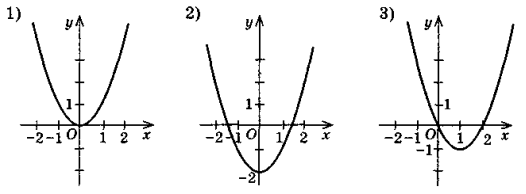
1) y = х²; 2) у = 2х²; 3) y = 2(x – 1)² + 1; 4) у = 2х²– 4х + 1.
Який із наведених графіків відповідає рівнянню у = х²– 2х? Відповідь обґрунтуйте.

VIII. Домашнє завдання

Вивчити означення квадратного рівняння, алгоритм побудови графіка квадратичної функції (див. опорний конспект).
Розв'язати вправи різного рівня складності на застосування вивченого алгоритму: №№ 11.3, 11.7.
Повторити властивості функції, формулу коренів квадратного рівняння.