Урок на тему: "Квадратична функція"

Тема: Квадратична функція

 

Мета: Закріпити вміння будувати графіки квадратичної функції і за графіком визначати її основні властивості ,  використовуючи властивості квадратичної функції розв'язувати завдання  підвищувати рівень навчальної мотивації з використанням комп'ютерних технологій , розвивати логічне мислення.

 

Обладнання:  ​​комп’ютери, планшети, смартфони, ПЗ  Advanced Grapher

 

Хід уроку:

 

         - Сьогодні у нас з вами не зовсім звичайний урок. Ми спробуємо об'єднати знання, отримані на уроках алгебри та інформатики і залучити комп'ютер до вирішення математичних завдань.

    - Отже , тема нашого уроку « Квадратична функція ». Ми вдосконалимо знання про квадратичну функцію

I. Заповни пропуски ... / повторення властивостей квадратичної функції / .

Отже, переходимо до першого етапу нашого уроку . Ви повинні заповнити пропуски , щоб вийшло вірне твердження або правильне формулювання визначення , правила.

 1 . Функція у = aх^2 + bx + c , де а , b , c - задані дійсні числа , а ≠ 0 , х - дійсна змінна, називається ... функцією.

2 . Графік функції у = aх^2 + bx + c при будь-якому а ≠ 0 називають ...

3 . Функція у = х^2 є ... ( зростаючою, спадною) на проміжку х < 0 .

4 . Значення х , при яких квадратична функція дорівнює нулю , називають ... функції .

5 . Точку перетину параболи з віссю симетрії називають ... параболи .

6 . При а > 0 вітки параболи у = aх^2 + bx + c спрямовані ....

II . Подумай ...

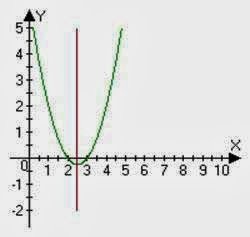
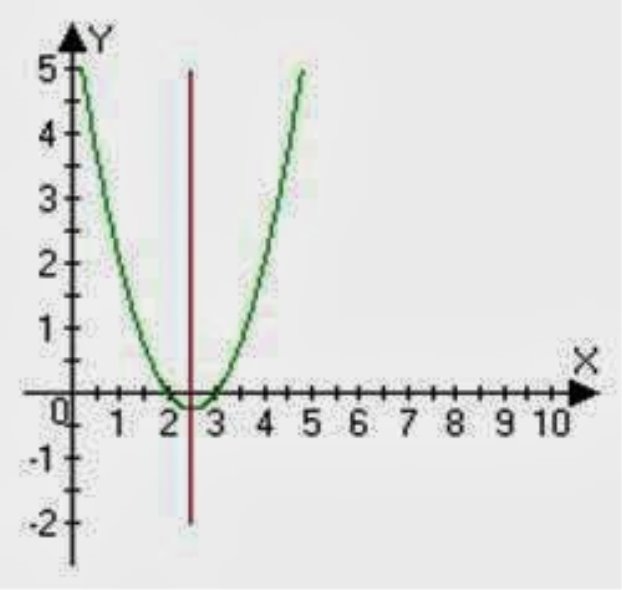
1 . Знайдіть координати вершини параболи у = х^2 -4х +4

2 . Знайдіть нулі квадратичної функції у = х^2 + х - 2

3 . Не виконуючи побудова графіка , визначте , найбільше або найменше значення приймає квадратична функція у = 2 - 5х- 3х^2

4 . За графіком знайдіть значення х , при яких значення функції

 у = х^2 - 5х + 6 додатні, від’ємні, дорівнюють нулю. Знайдіть проміжки зростання та спадання функції .

  III . Розв’яжи ... / робота в групах / .

 1 група: Знайти значення х , при яких квадратична функція

у = 2х^2 - 5х +3 приймає значення, рівне 1 .

 2 група: Знайдіть координати точок перетину параболи у = х^2 + х - 12 з осями координат.

 3 група: Не виконуючи побудова графіка функції у = х^2 - 4х + 6 , знайти її найбільше або найменше значення .

IV . Робота з програмою Advanced Grapher ...

Вам пропонується вирішити графічно нерівність x^2+ 2х - 3 > 5 .

V. Тест .

 

Варіант І: https://naurok.com.ua/test/kvadratichna-funkciya-35466.html

 

 

 

VI . Підсумок уроку . Д / з .  п. 11

 

Варіант ІІ: https://naurok.com.ua/test/kvadratichna-funkciya-variant-ii-35726.html

 

 

 

 

 

 

 

 

 

 

 

 

 

ДОДАТКИ :

Завдання по групах:

1 . Знайти значення х , при яких квадратична функція у = 2х2 - 5х +3 приймає значення, рівне 1 . Перевірити за допомогою програми Advanced Grapher

2 . Знайдіть координати точок перетину параболи у = х2 + х – 12 з осями координат. Перевірита за допомогою програми Advanced Grapher

3 . Не будуючи графік функції у = х2 - 4х + 6 , знайти її найбільше або найменше значення .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 . Знайти значення х , при яких квадратична функція у = 2х^2 - 5х +3 приймає значення, рівне 1 . Перевірити за допомогою програми Advanced Grapher

 

2 . Знайдіть координати точок перетину параболи у = х^2 + х – 12 з осями координат. Перевірити за допомогою програми Advanced Grapher

 

3 . Не будуючи графік функції у = х^2 - 4х + 6 , знайти її найбільше або найменше значення . Перевірити за допомогою програми Advanced Grapher

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 . Функція у = aх^2 + bx + c , де а , b , c - задані дійсні числа , а ≠ 0 , х - дійсна змінна, називається ............................................... функцією.

 

2 . Графік функції у = aх^2 + bx + c при будь-якому а ≠ 0 називають ..........................................

 

3 . Функція у = х2 є .......................... ( зростаючою, спадною) на проміжку х < 0 .

 

4 . Значення х , при яких квадратична функція дорівнює нулю , називають ........................ функції .

 

5 . Точку перетину параболи з віссю симетрії називають ............................. параболи .

 

6 . При а > 0 вітки параболи у = aх^2 + bx + c  спрямовані ...............................

 

 

 

 

 

 

 

 

 

 

 

1 . Знайдіть координати вершини параболи у = х2 -4х +4

 

 

 

 

 

 

 

 

 

 

2 . Знайдіть нулі квадратичної функції у = х2 + х – 2

 

 

 

 

 

 

 

 

 

 

 

 

3 . Не виконуючи побудова графіка , визначте , найбільше або найменше значення приймає квадратична функція у = 2 - 5х- 3х2

 

 

 

 

 

 

 

 

 

4 . За графіком знайдіть значення х , при яких значення функції

 у = х2 - 5х + 6 додатні, від’ємні, дорівнюють нулю. Знайдіть проміжки зростання та спадання функції