Урок на тему : "Нерівність трикутників"

Конспект уроку

Тема:  Нерівність трикутників

Мета: засвоєння змісту теореми, що виражає нерівність трикут­ника, і наслідок з неї; навчитися застосовувати теорему й наслідок під час розв'язування задачі; розвиток логіко-дидактичного мислення , вміння аналізувати, узагальнювати, виконувати дії за аналогією, створювати ситуацію успіху; виховувати почуття відповідальності, інтерес до предмета, уміння організовувати свою роботу.

Тип уроку:  засвоєння нових знань та вмінь.

Обладнання: набір креслярських інструментів, підручник геометрія 7 клас

(О.С.Істер).

Хід уроку

I. Організаційний етап

Учитель запрошує учнів до самоперевірки готовності до уроку.

II. Перевiрка домашнього завдання

  На даному етапі вчитель проходить і перевіряє наявність і правельність відповідей домашнього завдання.

III. Актуалізація опорних знань

Завдання класу(метод фронтального опитування)

 (використаємо метод «задачі за готовими малюнками»)

1. Визначте більший кут трикутника на малюнку. (слайд 1)

 

 

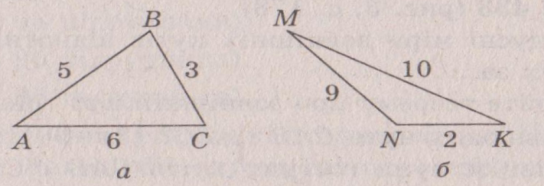
Відповідь: ∠В, ∠N.

 

 

 

 

 

 

2. Визначте більшу сторону трикутника на малюнку.(слайд 2)

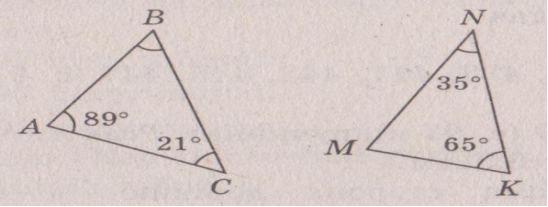
Відповідь: ВС,NK.

IV.Мотивація навчальної діяльності

Запропонуємо задачу.

Задача. Використавши циркуль та лінійку, побудуйте трикутник зі сторонами:

а) 3 см, 4 см, 5 см;

б) 3 см, 4 см, 1 см;

в) 3 см, 4 см, 8 см.

 

Порівняйте умови задач та виконані побудови. Що ви помітили?

 

Якщо учні володіють алгоритмом побудови трикутника за трьома сторонами, то вони швидко впораються із завданням а), а спроба виконання завдань б) і в) приведе їх до усвідомлення неможливості побудови трикутників з такими сторонами. Порівнявши дані задачі, учні помітять, що довжини двох сторін не змінюються, а значення довжини третього відрізка приводить у першому випадку до побудови трикутника, у другому — до виродженого трикутника, у третьому — до неможливості закінчити побудову. Із здобутого протиріччя формулюємо гіпотезу про існування певного зв’язку між трьома сторонами трикутника.

Пошук цього зв’язку — і є основною дидактичною метою уроку.

 

V.Пояснення нового матеріалу(з елементами евристичної бесіди)

(слайд 3)

Т е о р е м а  (нерівність трикутника). Кожна сторона трикутника      менша за суму двох інших сторін.

 

 

(слайд 4,5)

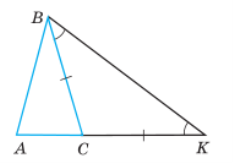                    Дано: ∆АВС

                    Довести : AB < AC + BC.

 

 

 

 

Д о в е д е н н я.

  Розглянемо довільний трикутник ABC і доведемо, що сторона трикутника, наприклад AB,  менша за суму двох інших сторін AC і CB.

1) Відкладемо на продовженні сторони AC відрізок CK, що дорівнює стороні BC. У рівнобедреному трикутнику BCK ∠ CBK = ∠ CKB.

2) ∠ ABK > ∠ CBK, тому ∠ ABK > ∠ AKB. Оскільки у трикутнику проти більшого кута лежить більша сторона, то AB < AK. Але ж AK = AC + CK = AC + BC. Отже,

AB < AC + BC.

Аналогічно можна довести, що AC < AB + BC, BC < AB + AC.

Теорему доведено.

 

(Слайд 6)

Н а с л і д о к. Кожна сторона трикутника більша за різницю двох інших сторін.

 

Д о в е д е н н я.

Віднявши від обох частин нерівності

AB < AC + BC, наприклад AC, матимемо AB – AC < BC. Отже, BC > AB – AC. Аналогічно маємо: AC > BC – AB, AB > BC – AC. Оскільки, наприклад, BC > AB – AC і BC > AC – AB, то, узагальнюючи, отримаємо BC > | AB – AC |.

З теореми про нерівність трикутника та наслідка з неї дістаємо важливе

співвідношення між сторонами трикутника:

кожна сторона трикутника менша за суму двох інших сторін, але більша від модуля їх різниці.

Наприклад, | AB – AC | < BC < AB + AC.

VI.Закріплення ЗУН

(Усно ) №495

Відповідь : 1)ні; 2)так; 3) так.

(Письмово )

 

 

 

№497 (слайд 7)

Дві сторони трикутника дорівнюють 2,9 см і 8,3 см. Якому найбільшому цілому числу сантиметрів може дорівнювати третя сторона?

Розв’язання :

 Нехай невідома сторона дорівнює а см. Тоді

<а<2,9+8,3

5,4<а<11,2

а= 11

Відповідь : 11 см.

№499

Чи можуть сторони трикутника бути пропорційними числам:

1)2,3,4

2)7,8,15

3)5,3,7

 

Розв’язання :

Нехай  коефіцієнтом пропорційності буде х см.

1)2х+3х>4х

   5х>4х-існує

Оскільки найменша сторона трикутника очевидно менша від суми двох інших сторін, то нерівність трикутника достатньо перевірити для найбільшої сторони.

2)Визначимо найбільшу сторону(15)

  Нехай  коефіцієнтом пропорційності буде х см.

  15х=5х+3х

  15х=15х-сторони не можуть бути пропорційні числам 7,8,15

3) Нехай  коефіцієнтом пропорційності буде х см.

    7х<5х+3х

    7х<8х-трикутник існує.

 

№501

Периметр рівнобедренного трикутника дорівнює 12 см. Чи може бічна сторона дорівнювати 3 см?

Розв’язання :

Ні,бо основа 12-(3+3)=6(см)

(Вчитель)

-Трикутник із сторонами 3 см,3 см і 6 см існує?

-Ні.Тому виконуватиметься рівність 6см=3см+3см

Відповідь: ні.

 

(слайд 8)

№502

Дві сторони рівнобедренного трикутника дорівнює 5 см і 11 см.Знайти периметр цього трикутника.

 

                                           Дано: ∆АВС,АВ=ВС

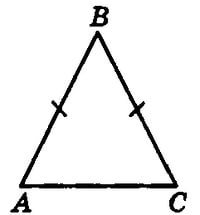           АВ=ВС= 11 см, АС=5 см

   Знайти :.

 

Розв’язання :

Бічна сторона дорівнює 11 см, оскільки ,якщо бічна сторона 5 см,а основа 11 см,то 11>5+5-виконується

Отже,=11+11+5=27(см)

Відповідь: 27 см.

 

№504

Периметр трикутника 80 см. Чи може  одна з його сторін дорівнювати :

1. 14 см;   2) 15 см;  3) 16 см?

                                          Розв’язання :

1)може,бо сума двох дорівнює

30-14=16(см)

І виконується нерівність 14<16,при умові, що сторона  14 см

найбільша.

2)не може,бо сума двох інших сторін теж 15 см.

3)не може,бо 30-16=14(см) і не виконується нерівність ,бо 16>14(одна сторона більша від суми двох інших).

Відповідь: 1)може; 2) не може; 3) не може.

 

 

 

VII. Домашнє завдання.

 Повторити §17-19 ,вивчити §20 ; виконати завдання на ст.117-18  (самостійна домашня робота№4 (1-12)).

Самостійна домашня робота №4

1.50°,60°,70°.                            В.

2.В.

3.90°-40°=50°                           В.

4.х+72°=180°

   х=108°                                   Б.

5.70°                                         Г.

6.<а<2,7+4,2

      1,5<а<6,9 А.

7.(х+30°)+х=90°

    2х=60°

     х=30°

90°-30°=60°

АС=4(см) (як катет проти кута 30°)

8.                                                                А.

9.Р=16 СМ

    А)16-8=8(см)        -

    Б)16-7,5=8,5(см)   -

    В)16-7=9(см)        +

    Г)16-2=14(см)        -

10.60°   А.

11.3х+5х+7х=180°

      15х=180°

       х=12°

∠1=3*12°=36°

∠2=5*12°=60°

∠3=7*12°=84° Г.

12.А.

VIII. Підведення підсумків. (слайд 9)

1.Сформулюйте теорему про нерівність трикутників(Кожна сторона трикутника      менша за суму двох інших сторін).

2.Сформулюйте наслідок з теореми (Кожна сторона трикутника більша за різницю двох інших сторін).