Урок на тему "Перетворення графіків функції"
Інтегрований урок з алгебри та інформатики
Тема уроку: Перетворення графіків функції
Мета уроку:
Навчальна:
- формувати розуміння змісту поняття «перетворення графіків функції» та вміння виконувати нескладні перетворення для побудови графіків функцій y=f(x)+b, y=f(x+a);
- навчити будувати графіки функцій однієї змінної, заданих у прямокутній системі координат, знаходити точки перетину двох графіків.
Розвивальна:
- Розвивати логічне мислення, увагу, уяву та навики самоконтролю;
Виховна:
- Виховувати графічну та алгоритмічну культуру.
Тип уроку: урок формування знань, умінь і навичок.
Обладнання та наочність: мультимедійний проектор, презентація, шаблони функцій ![]() , опорний конспект, програмне середовище «Graph».
, опорний конспект, програмне середовище «Graph».
Хід уроку
Математика – це мова природи
Дж. Гоббс
І. Організаційний момент
Доброго дня! Розпочинаємо наш урок. Урок нестандартний, інтегрований: математика та інформатика.
Епіграфом нашого уроку є слова «Математика – це мова природи».
ІІ. Повідомлення теми та мети уроку
Тема нашого уроку «Перетворення графіків функції». Постановка мети .
Мета нашого уроку: навчитись будувати графіки функцій однієї змінної, заданих у прямокутній системі координат, знаходити точки перетину двох графіків.
ІІІ. Мотивація навчальної діяльності
Розглянемо зображення мосту. В конструкції цієї інженерної споруди використані елементи у вигляді графіків відомих елементарних функцій: прямі лінії, параболи, гіперболи. Саме такі форми за інженерними розрахунками забезпечують міцність і надійність цієї споруди. В сучасній математиці вивченню функцій приділяється особлива увага, адже з їх допомогою можна змоделювати явища, які відбуваються в природі, на виробництві та в суспільстві. Побудова графіків значно полегшує процес вивчення функцій. А спробуємо навчитись будувати графіки деяких функцій швидко і легко.
В 7 класі ви вивчали такі теми: функція, графік функції, лінійна функція, її графік та властивості і т.д. Під час вивчення цих тем в основному виникає потреба в побудові графіків лінійних функцій . Що можна зробити досить легко і швидко у зошиті чи на дошці традиційними засобами. У курсі ж алгебри 8-го та 9-го класу ( не говорячи вже про 10-й та 11-й) передбачено вивчення функцій ![]() Отже, актуальність використання комп’ютерних засобів для роботи з функціями та їх графіками у 8-11 класах значно зростає.
Отже, актуальність використання комп’ютерних засобів для роботи з функціями та їх графіками у 8-11 класах значно зростає.
ІV. Актуалізація опорних знань
- Що називається функцією?
- Що називається графіком функції?
- Диктант
- Значення незалежної змінної називається … (аргумент)
- Значення залежної змінної … (значення функції)
- Всі значення аргументу називаються … (область визначення)
- Всі значення функції називаються … (область значення)
- Вісь Ох називається … (вісь абсцис)
- Вісь Оу називається … (вісь ординат)
- Графік квадратичної функції називається … (парабола)
Перевірка диктанту.
- Встановити відповідність
А) ![]()
Б) ![]()
В) ![]()
Г) ![]()
Д) ![]()
Е) ![]()
А) – 4; Г) – 2;
Б) – 5; Д) – 3;
В) – 1; Е) – 6.
V. Формування нових знань
Сьогодні ми з вами розглянемо програму Graph. Вона є засобом для побудови графіків функцій та роботи з ними, а також має багато додаткових можливостей. Наведемо деякі з них: побудова графіків функцій однієї змінної, заданих у прямокутній декартовій системі координат; побудова графіків функцій, заданих за допомогою рівнянь; знаходження координат точок перетину графіків двох функцій на заданому проміжку; знаходження нулів функції на заданому проміжку та інше. Програма Graph має свої особливості, для побудови графіку заданого функцією ![]() , в поле формули замість стандартного запису кореню потрібно ввести надпис SQRT, а для позначення степеня використовуємо символ ^ (наприклад, y = x^3, що означає
, в поле формули замість стандартного запису кореню потрібно ввести надпис SQRT, а для позначення степеня використовуємо символ ^ (наприклад, y = x^3, що означає ![]()
Побудуємо таблицю для побудови графіка функції ![]() і
і ![]() . Ми бачимо, що всі значення функції
. Ми бачимо, що всі значення функції ![]() на 2 більше, ніж у функції
на 2 більше, ніж у функції ![]() для відповідних аргументів. Це означає, що побудувавши графік функції
для відповідних аргументів. Це означає, що побудувавши графік функції ![]() ми можемо легко побудувати графік функції
ми можемо легко побудувати графік функції ![]() , піднявши його на 2 одиниці вгору (в направленні осі Оу).
, піднявши його на 2 одиниці вгору (в направленні осі Оу).
Побудова в Graph.
Можна також переконатись, як побудувати графік функції ![]() . Опустивши вниз графік функції
. Опустивши вниз графік функції ![]() на 2 одиниці ( в напрямі осі Оу, паралельне перенесення графіка).
на 2 одиниці ( в напрямі осі Оу, паралельне перенесення графіка).
Побудова в Graph.
Графік функції y = f(x) + b, можна отримати в результаті паралельного перенесення графіка функції y = f(x) уздовж осі у на b одиниць вгору, якщо b>0 і на b одиниць вниз, якщо b<0.
Приклад з функцією ![]() . Побудова в Graph. Побудова
. Побудова в Graph. Побудова ![]() +2 і
+2 і ![]() -2.
-2.
Також можна за допомогою графіку ![]() побудувати графік функції
побудувати графік функції ![]() і
і ![]() .
.
Побудова в Graph.
Графік функції ![]() можна одержати з графіка функції
можна одержати з графіка функції ![]() паралельним перенесенням вздовж осі абсцис на 2 одиниці вліво (відповідно пояснюємо побудову графіка функції
паралельним перенесенням вздовж осі абсцис на 2 одиниці вліво (відповідно пояснюємо побудову графіка функції ![]() .
.
Ці приклади показують, як за допомогою графіка функції у = f(x) можна побудувати графік функції ![]() .
.
Графік функції ![]() можна отримати в результаті паралельного перенесення графіка функції у = f(x) вздовж осі абсцис вправо на а одиниць , якщо а< 0 і вліво на а одиниць, якщо а >0.
можна отримати в результаті паралельного перенесення графіка функції у = f(x) вздовж осі абсцис вправо на а одиниць , якщо а< 0 і вліво на а одиниць, якщо а >0.
Приклад для функції ![]() , та
, та ![]() ,
, ![]()
Побудова в Graph.
VІ. Формування умінь і навичок
Вправа 1.
Графік якої функції отримаємо, якщо графік функції ![]() перенесемо
перенесемо
-
На 6 одиниць вгору
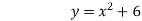
-
На 12 одиниць униз
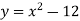
-
На 9 одиниць вправо
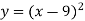
-
На 7 одиниць вліво
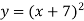
-
На 2 одиниці вправо і на 3 одиниці вниз
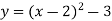
-
На 1 одиницю вліво і на 1 одиницю вгору
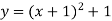
Перевірка в програмі Graph.
Вправа 2.
Побудова графіків функції за шаблоном і в програмі Graph.
Побудова в програмі Graph.
Вправа 3.
Розв’язати графічно рівняння ![]()
-
Будуємо графік функції
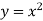 .
.
-
Будуємо графік функції
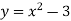 .
.
-
Будуємо графік функції
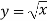 .
.
-
Будуємо графік функції
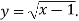
- Визначаємо розв’язок х = 2.
VII. Підсумок уроку
Мікрофон
- Що ми вивчали на сьогоднішньому уроці?
-
Як побудувати графік функції
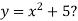
-
Як побудувати графік функції
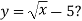
-
Як побудувати графік функції
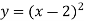 ?
?
-
Як побудувати графік функції
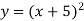 ?
?
Ми з вами сьогодні навчились будувати графіки функцій в програмі Graph. Ви напевно помітили, що завдяки цій програмі економиться час на уроці. Ця програма ефективний засіб для побудови та розв’язуванні графіків функцій.
VIIІ. Домашнє завдання
-
Побудувати в програмі Graph функції
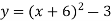 ,
, 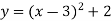 ,
, 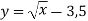 ,
, 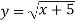 .
.
-
Розв’язати графічно рівняння
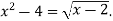


про публікацію авторської розробки
Додати розробку
