Міністерство охорони здоров’я України

Комунальний заклад

Бериславський медичний коледж

Херсонської обласної ради

Методична розробка

Тема:” Похідна функції в точці. ”

Навчальна дисципліна: «математика».

Спеціальність: 5.12020101 «Фармація»

Курс:                                    ІI

Кількість годин:                  90 хв

Автор: Гуліда С.І. викладач вищої категорії дисципліни: математика.

                                                                  Розглянуто та затверджено,

                                             на засіданні  циклової комісії
                                           загальноосвітньої підготовки

                                                                  Протокол № 

                                                                  від  «  »               20    р.

                                                                  Голова комісії:                Л. І. Драган

                                             м. Берислав

Предмет                    математика

Тема заняття           Похідна функції в точці.

Мета заняття:

Освітня     Засвоїти поняття: похідної функції в точці. Познайомити учнів з правилами знаходження найпростіших похідних.

Виховна    Виховувати наполегливість, уважність, культуру математичних записів

Розвивальна     Розвивати логічне мислення, увагу, мову

Методи: словесні, наочні, практичні

Тип заняття: засвоєння нових знань

                                     Структура заняття і розрахунок часу

Організаційна частина –                                                                                  1хв.

Перевірка домашнього завдання, перевірка раніше засвоєних знань –      15хв.

Актуалізація знань –                                                                                         3хв.

Мотивація навчальної роботи. Повідомлення теми та мети заняття –        1хв.

Вивчення нового матеріалу. (Сприймання та осмислення студентами нового навчального матеріалу) –                                                                                  40хв.

Узагальнення і систематизація виучуваного матеріалу –                              5хв.

Закріплення матеріалу –                                                                                    20хв.

Домашнє завдання –                                                                                           2хв.

Підведення підсумків заняття -                                                                         3хв.

                                Забезпечення заняття

А. Наочні посібники – графіки функцій

Б. Роздатковий матеріал – картки

В. Технічні засоби навчання – ПК, РК панель.

Міжпредметні та внутрішньопредметні зв’язки:

Забезпечуючі – математика

Забезпечувані – фізика, хімія

Внутрішньопредметні зв’язки –

1.Функції.

2.Неперервні функції.

3.Похідна суми, добутку, частки, складеної функції

4.Найбільше та найменше значення функції

5.Інтеграл та його застосування

І. Перевірка домашнього завдання.

1.Фронтальне опитування.

1.Що таке функція?

2. Яка функція називається неперервною?

3. Як знаходиться границя суми, добутку, частки?

4.Які основні теореми про неперервність функції?

5.Яка функція називається неперервною на інтервалі?

6. Як знаходиться модуль суми, добутку, частки?

7.Які основні умови неперервності функції в точці?

1. Фронтальна бесіда за запитаннями № 1-5, 7-9 із “Запитання і завдання для повторення” розділу VII.
2. Перевірка правильності виконання домашніх вправ за записами на дошці, зробленими перед уроком:

№ 2

=

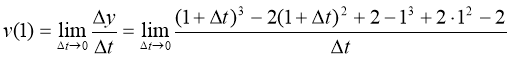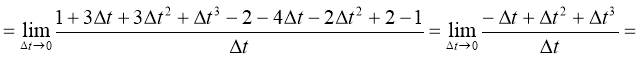
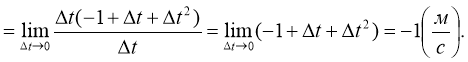
№ 9

.

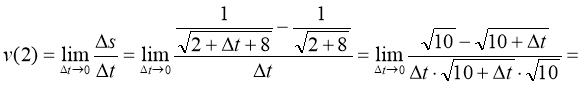
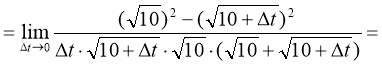
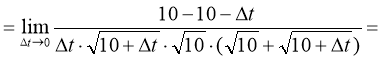
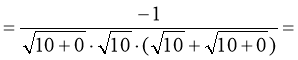
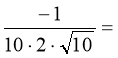
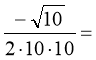
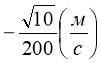3. Відповіді на запитання, що виникли у учнів під час виконання домашніх вправ.

До відкриття похідної незалежно один від одного прийшли два відомих вчених Ісаак Ньютон та Го́тфрід Вільгельм Лейбніц наприкінці 17 століття. Ньютон, означаючи похідну, виходив із задач механіки; Лейбніц - із геометричних задач. Але відкриттю похідної і основ диференціального числення передували роботи таких великих вчених як П’єра  Ферма та Рене Декарта. Так у "Початках" Евкліда описано спосіб побудови дотичної до кола,  Архімед побудував дотичну до спіралі, що носить його ім'я, Аполлоній - до еліпса, гіперболи і параболи. Однак давньогрецькі вчені не вирішили задачу до кінця, тобто не знайшли загального методу, придатного для побудови дотичної до будь-якої плоскої кривої в даній точці. Перший загальний спосіб побудови дотичної до алгебраїчної кривої був викладений у "Геометрії" Декарта. Більш загальним і важливим для розвитку диференціального числення був метод побудови дотичних Ферма. Хоча сам термін «похідної» і позначення ввів Жозеф Лагранж.

Поняття похідної виникло у ХVІІ ст. у зв’язку з необхідністю розв’язати деякі математичні і фізичні задачі. Задачу про побудову дотичної розв’язав Г.Лейбніц, про визначення миттєвої швидкості під час прямолінійного нерівномірного руху-І.Ньютон, який прийшов до поняття похідної, виходячи з положень механіки. Результати  своїх досліджень І.Ньютон виклав у трактаті „Метод флюксій”, опублікованому в 1736 році. Учений називав похідну флюксією, а саму функцію – флюентою.

Похідна – це швидкість зміни функції. Нехай матеріальна точка рухається вздовж координатної прямої х за законом х=х(t). Тоді похідна від координати за часом у даний момент є швидкістю руху в цей момент часу. У цьому й полягає її механічний зміст.

Поняття похідної як швидкості зміни функції використовується під час означень багатьох фізичних величин. Наприклад, похідна швидкості руху за часом є прискорення; похідна величини заряду за часом є сила струму; похідна потоку магнітної індукції за часом є електрорушійна сила індукції; похідна роботи за часом є потужність.

Іноді може виникнути запитання: для чого потрібна похідна? Може її вигадали вчені тільки для того, щоб похизуватись знаннями неї перед іншими? А може це „гола” теорія і все?

Як ми переконались, похідна широко використовується у фізиці. Крім того, що з її допомогою проводять дослідження функції на зростання і спадання, екстремуми, найбільше і найменше значення. Наприклад, якщо f ′(x)>0 в кожній точці інтервалу І, то функція f(x) зростає на цьому інтервалі; якщо  f′(x)<0 в кожній точці інтервалу І, то функція спадає на цьому інтервалі.

А як поводить себе функція в точках, в яких похідна не існує, або дорівнює 0, тобто в критичних точках, і що є необхідною умовою екстремуму? Умова існування екстремуму в точці така:

Якщо в критичній точці х₀ похідна змінює знак з „плюса” на „мінус”, то х₀ – точка максимуму, якщо змінює знак з „мінус” на „плюс”, то х₀ – точка мінімуму.

                          Задача  Дідони.

Фінікійська царівна Дідона, рятуючись від переслідувань свого брата, відправилася на захід вздовж берегів Середземного моря, де шукала собі пристановища. На узбережжі Туніської затоки вона почала вести переговори з Ярбом про купівлю для себе землі. І попросила вона зовсім мало – стільки, скільки можна „обгородити шкірою з бика” . І коли Дідона і Ярб дійшли згоди, Дідона порізала шкіру бика на тоненькі смужки, зв’язала їх і обгородила ними велику територію, чого Ярб не чекав. На ній Дідона побудувала фортецю, а поблизу неї – місто Карфаген.

Хіба не дивно, що в ті далекі часи ставились і розв’язувались такі цікаві, складні і досить проблемні задачі?

То ж поміркуймо, яку найбільшу кількість землі можна обгородити шкірою з бика? Або, мовою математики, яка із замкнених кривих, що має задану довжину, може охопити найбільшу площу? Фактично, нам треба знайти найбільше значення деякої неперервної функції на відрізку.

Цю класичну задачу сама Дідона розв’язала правильно. А кривою, що охоплює найбільшу площу, є круг – найдосконаліша, на думку Піфагора, плоска фігура.

II. Сприймання і усвідомлення поняття похідної.

На попередньому уроці ми розглянули розв'язування двох задач: знаходження миттєвої швидкості та знаходження кутового коефіцієнта дотичної. Ці дві задачі розв'язуються одним і тим самим способом, який складається з таких етапів:

1) незалежній змінній х надаємо приросту Δх;

2) знаходимо приріст залежної змінної — Δу;

3) знаходимо відношення ;

4) знаходимо .

використовується при розв’язуванні і інших важливих задач (зокрема, про швидкість протікання хімічних реакцій, знаходження густини неоднорідного стержня, теплоємності тіла при нагріванні, сили змінного струму в провіднику та інш.), тому доцільно всебічно вивчити властивості цієї границі, зокрема, вказати способи її обчислення.

Нехай задано функцію у = f(x) на деякому проміжку. Візьмемо довільну внутрішню точку х_о даного проміжку, надамо значенню х_о довільного приросту Δх (число Δх може бути як додатним, так і від'ємним), але такого, щоб точка х_о+Δх належала даному проміжку, тоді

1) Обчислимо в точці х_о приріст Δу = Δf(х_о) функції:

Δу = Δf(х_о) = f(x_o+ Δх) – f(х_о);

2) Складемо відношення: .

3) Знайдемо границю цього відношення при умові, що Δх → 0, тобто:

Якщо дана границя існує, то її називають похідною функції у = f(x) в точці х_о і позначають f '(х_о) або у' (читається еф штрих від х_о або у штрих).

Похідною функції у = f(x) в точці х_о називається границя відношення приросту функції до приросту аргументу при умові, що приріст аргументу прямує до нуля, а границя існує, тобто

.

Приклад 1. Знайдіть похідну функції f(x) = Зх² + 2 в точці х_о.

Розв'язання

Знайдемо приріст функції:

Δf = f(х_о + Δx) – f(x_o) = 3(х_о + Δx)² + 2 - 3 - 2 =

= 3 + бх_оΔx+ 3Δx² + 2 - 3 - 2 = 6х_оΔх+ 3Δx² = Δx(6x_ο + 3Δx).

Знайдемо відношення приросту функції до приросту аргументу:

.

Знайдемо похідну даної функції в точці х₀:

f '(х_o) = = = 6х_о + 3 · 0 = 6х_о.

Відповідь: 6х_о.

Приклад 2. Знайдіть похідну функції f(x) = kx + b (k і b постійні) у точці x_o.

Розв'язання

Знайдемо приріст функції:

Δf = f(х_о + Δx) – f(x_o) = k(x_o + Δx) + b - kx_o - b = kx_o + kΔx - kx_o = kΔx.

Знайдемо відношення приросту функції до приросту аргументу:

Отже, f '(х_o) = = = k, або (kx + b)' = k.

Відповідь: k.

З другого прикладу можна зробити висновок, що похідна лінійної функції є постійна величина, яка дорівнює кутовому коефіцієнту прямої. Якщо в формулі (kx + b)' = k покласти k = 0, b = C, де С — довільна постійна, то одержимо, що С' = 0, тобто похідна постійної дорівнює нулю.

Якщо в формулі покласти k = 1, b = 0, то одержимо х' = 1.

Функцію, яка має похідну в точці х_о, називають диференційованою в цій точці.

Функцію, яка має похідну в кожній точці деякого проміжку, називають диференційованою на цьому проміжку. Операція знаходження похідної називається диференціюванням.

Нехай D₁ — множина точок, у яких функція у = f(x) диферен­ційована. Якщо кожному хD₁ поставити у відповідність число f'(x), то одержимо нову функцію з областю визначення – D₁. Цю функцію позначають f':

Виконання вправ

1. Користуючись означенням похідної, знайдіть похідну функції f, якщо:

а) f(x) = х² + 1 в точці 1;  б) f(x) = х³ в точці 1;  

в) f(x) = в точці 1;   г) f(x) = в точці 1.

Відповідь: а) 2;         б) 3;        в) -1;       г) .

2. Користуючись означенням похідної, знайдіть f'(x), якщо:

a) f(x) = 2х + 3;       б) f(x) = х² + х;

в) f(x) = 5х² + 6х;    г) f(x) = 3х² + 5х + 6.

Відповідь: а) 2;        б) 2х + 1;   в) 10х + 6; г) 6х + 5.

3. За допомогою формули (kx + b)' = k, знайдіть похідні функції:

a) f(x) = 3х + 4;       б) f(x) = 6х - 1;

в) f(x) = 10;           г) f(x) = 5х.

Відповідь: а) 3;         б) 6;        в) 0;        г) 5.

III. Сприймання і усвідомлення механічного змісту похідної.

На попередньому уроці ми розглядали задачу про знаходження миттєвої швидкості прямолінійного руху матеріальної точки. Порівнюючи одержані результати з означенням похідної, можна зробити висновок: якщо матеріальна точка рухається прямо­лінійно і її координата змінюється по закону s = s(t), то швидкість її руху v(t) в момент часу t дорівнює похідній s'(t):

v(t) = s'(t).

Виконання вправ

1. Точка рухається по закону s(t) = 1 + 2t² (м). Знайдіть швидкість руху точки в момент часу t = 1 с.

Відповідь: 4 .

2. Знайдіть миттєву швидкість руху точки, якщо:

a) s(t) = 3t + 1;      б) s(t) = 3 – 2t;  в) s(t)=t²·,          г)s(t) = 3t².

Відповідь: а) 3;         б) -2;       в) 5t;       г) 6t.

3. Точка рухається прямолінійно за законом s(t) = 2t³ — 3t (s — шлях в метрах, t — час в секундах). Обчисліть швидкість руху точки:

а) в момент часу t;  б) в момент t = 2 с.

Відповідь: а) (6t² – 3);     б) 21.

4. Рух точки відбувається за законом s(t) = t² – 4t + 6. У який момент часу швидкість руху дорівнює: а) 0; б) 10?

Відповідь: а) t = 2;    б) t = 7.

IV. Сприймання і усвідомлення геометричного змісту похідної, рівняння дотичної.

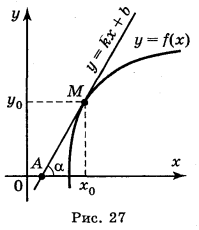На попередньому уроці ми розглядали задачу про знаходження кутового коефіцієнта дотичної. Порівнюючи одержані резуль­тати з означенням похідної, можна зробити висновок: значення похідної функції у = f(x) в точці xo до­рівнює кутовому коефіцієнту дотичної до графіка функції в точці з абсцисою xo : f'(xo) = k = tg α (рис. 27)

Розглянемо функцію у = f(x). Її гра­фік зображено на рис. 27.

У точці М(x_o;y_o) проведено дотичну до кривої      у=f(x). Складемо рівняння дотичної AM, знаючи координати точки М(x_o;y_o) дотику і рівняння у = f(x) кри­вої. Дотична — це пряма. Рівняння будь-якої прямої має вигляд: у = kx + b. Оскільки k = f'(x_o), тому рівняння дотичної має вигляд:

у = f'(x_o)x + b.                           (1)

Знайдемо b, виходячи з того, що дотична проходить через точку М(x_o;y_o) і тому її координати задовольняють рівнянню дотичної:

у_о = f '(х_o) · х_o + b, звідси b = у_o – f '(x_o) · x_o.

Тепер підставимо значення b в рівняння (1) дотичної і одер­жимо:

у = f '(x_o) ·x + у_о – f '(x_o) · x_o   y – y_о = f '(x_о )(x – x_o)·

Отже, рівняння дотичної до кривої у = f(x) в точці М(x_o; у_o) має вигляд:

y – y_о =  f '(x_o)(x – x_o).                         (2)

Рівняння дотичної до кривої у = f(x) у заданій точці x_o можна знаходити за таким планом (схемою):

1. Записуємо рівняння (2) дотичної:  y – y_о =  f '(x_o)(x – x_o).   

2. Знаходимо у_o = f(x_o)·

3. Знаходимо значення f '(x) у точці x_o: f '(x_o).

4. Підставляємо значення x_o, y_o і f '(x_o) y рівняння (2).

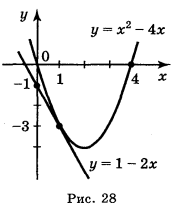
Приклад 1. Складіть рівняння дотичної до графіка функції у = х² - 4х в точці x_o = 1. Виконайте схематичний рисунок.

Розв'язання

1.     y - y_о =  f '(x_o)(x – x_o) — рівняння шуканої дотичної.
2.     у_o= 1² – 4·1 = 1 – 4 = - 3.
3. .

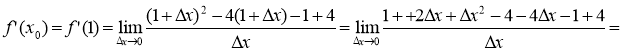
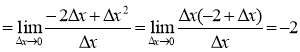4. Підставляємо значення x_o = 1, y_o = –3, f'(x_o) = –2              у рівняння дотичної: y + 3 = –2(x – 1), або у = – 3 – 2x + 2, або y = –1 – 2х (рис. 28).

Виконання вправ.______________

1. Дотична до графіка функції у = f(x) у точці з абсцисою x_o утворює з додатним напрямом осі ОХ кут 45°. Знайдіть f'(x_о).

Відповідь: 1.

2. Відомо, що тангенс кута нахилу дотичної до графіка функції у = f(x) в точці з абсцисою х_o = –1 дорівнює 3. Запишіть рів­няння дотичної до графіка функції в цій точці, якщо f(x_o) ⁼ 2.

Відповідь: у = 3x + 5.

3. Який кут (гострий чи тупий) утворює з додатним напрямом осі ОХ дотична до графіка функції: а) у = х² + 2х в точці x = 1;  б) у = х² + 2х в точці x = -27

Відповідь: а) гострий;  б) тупий.

4. Запишіть рівняння дотичної до параболи у = 3х² - 2 у точці:

а) x_o = -2;          б) x_o = 0;           в) x_o = 1.

Відповіді: а) у = - 12х - 14;   б) у = -2;    в) у = 6х - 5.

V. Підведення підсумків уроку.

       Я переконався, що ви – група однодумців, які вміють застосовувати набуті знання, а це означає, що кожний з вас, як і сьогодні,  так і в майбутньому буде компетентний в певній галузі.

 Думаю, уміння аналізувати ситуацію ще не раз стане вам у нагоді.

VI. Домашнє завдання.

Розділ VII § 2. Запитання і завдання для повторення до розділу VII № 11—17. Вправи № 1 (1, 2), 3.