Урок з алгебри в 9-му класі.

Розроблено та проведено вчителем математики

 ЗОШ № 7 ім. В. В. Бражевського м. Житомира

Сергієм Олександровичем Сафонюком

                  

 

 

Епіграф уроку

Якщо ви володієте знанням, дайте іншим                                                                             запалити від нього свої світильники. Т. Фулпер

 

 

 

 

 

 

 

Актуалізація знань, вмінь та навичок учнів

 

Знайти відповідність між твердженнями (1-8) та математичними формулами (А – І)

 

 

 

1.  Арифметична прогресія                                                          А     

2.  Геометрична прогресія                                                            Б     

3.  Сума перших n членів арифметичної прогресії                    В     𝟑; 𝟔; 𝟏𝟐; …

4.  Властивість геометричної прогресії                                       Г     

5.  Сума нескінченної спадної геометричної прогресії             Д      

6.  Властивість арифметичної прогресії                                      Е      4; 12; 20;…

7.  Формула n-го члена геометричної прогресії                         Ж     𝒃_𝒏 = √𝒃_𝒏−𝟏 ∙ 𝒃_𝒏+𝟏       8. Формула n-го члена арифметичної прогресії                        З      

І     𝒂_𝒏 = 𝒂_𝟏 + 𝒅(𝒏 − 𝟏)

 

Правильні відповіді: 1 – Е; 2 – В; 3 – Д; 4 – Ж; 5 – Б; 6 – А; 7 – Г; 8 – І.

 

Далі проводиться захист-розв’язок учнями своїх задач, які вони знайшли

Задача № 1

 

Розв’язування

Так як кожний наступний чоловік отримує на   міри зерна більше, ніж попередній, то маємо арифметичну прогресію з . Використовуючи формулу для суми

, складемо рівняння :  

 

Відповідь: міри зерна.

Примітка:  давні єгиптяни розв’язували дану задачу (мовою сучасної алгебри) за допомогою такої формули:  , яку пропонуємо вам вивести самостійно з відомої формули.

 

Задача № 2

Розв’язання

Як бачимо, кожний наступний цвях в 2 рази дорожчий за попередній. Отже, маємо зростаючу геометричну прогресію, в якій: (вартість 1-го, 2-го та 3-го цвяхів відповідно); знаменник ; членів прогресії ( цвяхів ) n = 24. Необхідно знайти 𝑆₂₄, тобто скільки заплатили за цвяхи, а потім дати відповідь на питання задачі.

Використовуємо формулу для знаходження суми перших n членів зростаючої геометричної

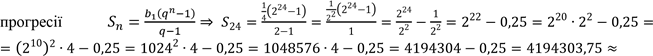
≈ 1943,04 (крб.) Ми знайшли вартість 24-х цвяхів. Вважаючи, що за коня треба було віддати 156 крб., знайдемо на скільки покупець проторгувавсь: 41943,04 – 156 = 41943,04 (крб.) Відповідь: на 41943,04 крб.

Задача № 3

Розв’язування

Маємо: людей – 7, котів – 7 ^. 7 = 7², мишей – 7^{2 .} 7 = 7³, колосків – 7^{3 .} 7 = 7⁴, зерна – 7^{4 .} 7 = 7⁵. 

Дана послідовність: 7, 7², 7³, 7⁴, 7⁵ є зростаючою геометричною прогресією, де 𝑏₁ = 7,  𝑞 = 7, 𝑛 = 5. Потрібно знайти суму п’яти членів цієї прогресії 𝑆₅. Знайдемо числа цього ряду: 𝑏₁ = 7; 𝑏₂ = 49; 𝑏₃ = 343; 𝑏₄ = 2401; 𝑏₅ = 16807. Суму цих чисел можна знайти:

1)     безпосередньо їх додавши – 7+49+343+2401+16807=19607 (мір) – зерна;

                                                                                          5                                5

2)     використавши формулу - 

Відповідь: а) числовий ряд: 7; 49; 343; 2401; 16807; б) сума: 19607

Задача № 4

Розв’язування

 Так як після кожного руху поршня насоса повітря стає на 20%  менше ніж було, тобто 80% від попередньої кількості, то можемо стверджувати, що числа, якими виражають тиск, утворюють спадну геометричну прогресію з 𝑏₁ = 760; 𝑞 = 0,8; 𝑛 = 7. Потрібно знайти 𝑏₇.   Враховуючи, що 𝑏_𝑛 = 𝑏 ∙ 𝑞^𝑛−1, отримаємо: 𝑏₇ = 760 ∙ 0,8⁶ = 760 ∙ 0,262144 = 199,23 .

Відповідь: ≈200 мм рт.ст. 

Задача № 5

                            

Розв’язування

За 1-й рік осетер відкладає 300000 ікринок, за 2 роки – 600000 ікринок, за 3 роки – 900000 ікринок і т.д. Це не що інше як арифметична прогресія, де 𝑎₁ = 300000, 𝑑 = 300000 . Потрібно знайти кількість всіх ікринок за 10 років для одного осетра, тобто 𝑆₁₀ і результат помножити на 3. 

 

Тоді 3 ∙ 𝑆₁₀ = 16500000 ∙ 3 = 49500000 (ікринок) – 3 самки за 10 років Відповідь: 49500000 ікринок 

Задача № 6

Розв’язування

Згідно умови задачі гальмівний шлях за першу секунду складає 15 м, за другу секунду на 3 м менше, тобто 12 м, за третю – 9 м і т.д., доки автомобіль не зупиниться. Отже, гальмівний шлях – це не що інше, як арифметична прогресія, де 𝑎₁ = 15, 𝑎₂ = 12, 𝑎₃ = 9, … , 𝑎_𝑛 = 0, 𝑑 = 𝑎₂ − 𝑎₁ = 12 − 15 = −3. Знайдемо n – час гальмування та 𝑆_𝑛 - шлях гальмування.

Застосуємо формулу для знаходження n-го члена прогресії та підставимо числові значення.

𝑎_𝑛 = 𝑎₁ + 𝑑(𝑛 − 1) ⟹ 15 − 3(𝑛 − 1) = 0 ⇔ 3(𝑛 − 1) = 15 ⟹ 𝑛 − 1 = 5 ⟹ 𝑛 = 6 (с) – час гальмування автомобіля. Для знаходження гальмівного шляху використаємо наступну формулу:  

Відповідь: 45 м

Задача № 7

 

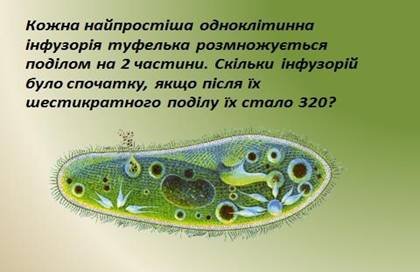
Розв’язування

Якщо після кожного поділу кількість інфузорій збільшується вдвічі, то він (поділ) утворює геометричну прогресію, в якій 𝑏₁ = 𝑥, 𝑞 = 2, 𝑏₇ = 320 (320 інфузорій стало після 6-го поділу) Використаємо формулу для n-го члена геометричної прогресії: 𝑏_𝑛 = 𝑏₁ ∙ 𝑞^𝑛−1. Маємо 𝑏₇ = 𝑏₁ ∙ 𝑞⁶ ⟹ 𝑥 ∙ 2⁶ = 320 ⟹ 64𝑥 = 320 ⟹ 𝑥 = 320: 64 ⟹ 𝑥 = 5 – інфузорій. 

Відповідь: 5 інфузорій  туфельок.

Задача № 8

Розв’язування

Приймемо за x число, яке вказує в скільки раз збільшувалась продуктивність праці екскаватора. Тоді математична модель задачі набуде вигляду: 1-го дня вийнято 4800 м³ землі, 2-го - 4800 x м³, а 3-го - 48000 x² м³. Всього за три дні вийняли 18300 м³. Маємо геометричну прогресію, де 𝑏₁ = 4800, 𝑞 = 𝑥, 𝑆₃ = 18300. Необхідно знайти 𝑏₃. Знайдемо знаменник 𝑞.

                                                                 ( ³ )                                                                               ( ²                 )

 

√

Оскільки продуктивність праці невід’ємна, то q = 1,25. 𝑏₃ = 𝑏₁𝑞² = 4800 ∙ 1,25² = 7500 (м³).

Відповідь: 7500 м³

Задача № 9

Розв’язування

Вартість кожної наступної вівці більше у 2 рази, ніж попередньої. Тому маємо класичну зростаючу геометричну прогресію з . Треба знайти 𝑆₂₀.

( крб. ) Відповідь: 1048576 крб. 

Задача № 10

 

Розв’язування

Задача на збільшення еритроцитів на однакову кількість – це задача на арифметичну прогресію. Встановимо скільки раз відбудеться це збільшення 4800: 600 = 8 (разів). Отже: 𝑎₁ = 5, 𝑑 = 1, 𝑎₉ =? Маємо: 𝑎_𝑛 = 𝑎₁ + 𝑑(𝑛 − 1) ⇒ 𝑎₉ = 𝑎₁ + 8𝑑 = 5 + 8 ∙ 1 = 13 (млн.)

Відповідь: на висоті 4800 м кількість еритроцитів становитиме 13 млн.

 

Задача № 11

 

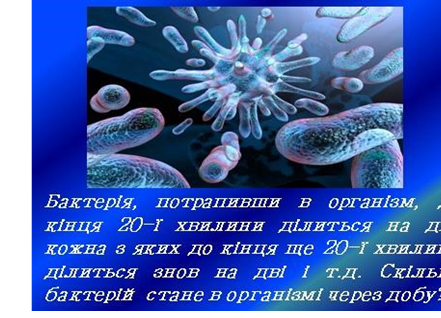
Розв’язування

Спочатку була 1-на бактерія, через 20 хвилин – 2 бактерії, ще через 20 хвилин – 4 бактерії і т.д., тобто маємо зростаючу геометричну прогресію, де: 𝑏₁ = 1, 𝑞 = 2. Для знаходження загальної кількості бактерій, тобто 𝑆_𝑛, необхідно знати n. В добі 24 години, а це 1440 хвилин.

1440: 20 = 72 - двадцятихвилинок в добі. Отже, n  

= 2⁷³ − 1 = 9444732965739290427391 - бактерій. 

Відповідь: 9,4 ∙ 10²¹ бактерій.

Задача № 12

 

Розв’язування

Дана задача є задачею на арифметичну прогресією, в якій 𝑎₁ = 30, 𝑑 = 20, 𝑆₁₂ =? 

(грн.) 

Відповідь: 1680 грн.

Задача № 13

                                

Розв’язування

З курсу фізики відомо,що при вільному падінні , де 𝑎 = 490 м, .

Скориставшись цією формулою знайдемо час:  

Цю задачу можна розв’язати за допомогою арифметичної прогресії, в якій 𝑎₁ = 4,9; 𝑑 = 9,8  

𝑆_𝑛 = 490, де n – час падіння. Отже:  

⇒ 9,8𝑛² = 980 ⇒ 𝑛² = 100 ⇒ 𝑛 = ±10. Враховуючи, що n – час падіння, маємо 𝑛 = 10.

Відповідь: 10 с.

 

 

 

Задача № 14

Розв’язування

Будемо вважати, що з кожної насінини виростає квітка, яка в свою чергу дає 1500 насінин, тобто запас насіння збільшується у 1500 раз. Маємо зростаючу геометричну прогресію, у якій Застосовуємо відому формулу для суми перших членів прогресії:  (насінин).

Відповідь: ≈ 5,1 ∙ 10¹² насінин.

Задача № 15

Розв’язування

Велосипедист за 3 год. проїхав 45 км, а тоді виїхав мотоцикліст, початкова швидкість якого була 44,75 км/год і потім щогодини збільшувалась на 1 км/год, тобто утворюється зростаюча арифметична прогресія з 𝑎₁ = 44,75, 𝑑 = 1. Шлях, який проїхали велосипедист і мотоцикліст позначимо через 𝑆_𝑛, де n – час, через який мотоцикліст наздогнав велосипедиста. Шлях велосипедиста - 𝑆_𝑛 = 45 + 15𝑛 , шлях мотоцикліста -. Прирівняємо праві частини:  

 

𝑛₂ = −60. Оскільки n – це час, який не може набувати від’ємних значень, то відповіддю задачі є n = 1,5 години. Відповідь: 1 год 30 хв 

 

Задача № 16

Розв’язування

Кожний наступний крок учня в 2 рази менше за попередній, тому маємо спадну геометричну прогресію з 𝑏₁ = 1, 𝑞 = 0,5. Знайдемо який шлях пройде учень, тобто суму довжин його кроків Для спадної геометричної прогресії маємо:(м). Зробимо висновок: максимально можлива відстань, яку за даних умов може пройти учень, дорівнює 2 метри.

Тобто, учень не дійте до столу вчителя.

Задача № 17

Розв’язування

За першу хвилину треба сплатити 33 копійки, за другу – 30 копійок, за третю – 27 копійок і т.д. Це спадна арифметична прогресія, в якій 𝑎₁ = 33, 𝑑 = −3, 𝑆₇ =? Використовуємо відому формулу:   ( грн. )

Відповідь: 1,68 грн.

Задача № 18

Розв'язування

Зростання кількості побитих яєць у 2 рази в кожному наступному лотку дає нам геометричну прогресію, де 𝑏₁ = 2, 𝑞 = 2, 𝑏_𝑛 = 64 (𝑏_𝑛 - останній лоток, n – кількість лотків ). Треба знайти n. 𝑏_𝑛 = 𝑏₁𝑞^𝑛−1 ⇒ 64 = 2 ∙ 2^𝑛−1 ⇒ 2^𝑛 = 2⁶ ⇒ 𝑛 = 6.

Відповідь: 6 лотків.

Задача № 19

Розв’язування

У першого онука було 195 грибів, у наступного на 10 менше, тобто 185 грибів і т.д. Кількість грибів у кожного онука є числа, які утворюють спадну арифметичну прогресію, в якій:  𝑎₁ = 195, 𝑑 = −10. Тоді у 15-го онука в кошику буде 𝑎₁₅ = 195 − 10 ∙ (15 − 1) = 55 (грибів).

Всього у онуків буде (грибів), а разом з дідом у них буде 1875 + 200 = 2075 грибів.

Відповідь: 2075 грибів.

Ось такі задачі знаходили та розв’язували учні 9-го класу з допрофільним вивченням математики на уроці-підсумку (пара) по темі «Прогресії». Учнівський захист задач обов’язково оцінювався вчителем та експертною групою, яка складалась з усіх учнів, які готували презентацію. Критерій оцінювання може бути різним в залежності від підготовленості та структури учнівського колективу. Наприклад для даного уроку було розроблено наступний критерій оцінювання: 1) змістовність та цікавість задачі 1 – 5 балів;  2) зв’язок з навколишнім світом 1 – 10 балів; 3) оформлення та подача презентації 1 – 5 балів;

40) розв’язування та пояснення 1 – 10 балів. Виходячи с цього була розроблена сітка оцінок

Бали за захист	Оцінка по 12-бальній шкалі
5 – 9 балів	7
10 -14 балів	8
15 -19 балів	9
20 – 24 бали	10
25 – 29 балів	11
30 балів	12

 

ПРОГРЕСІЯ ТА ЛІТЕРАТУРА