Урок на тему "Тригонометрія-одна із найцікавіших розділів Алгебри” (брейн-ринг)
 ДНЗ «Мукачівський професійний ліцей»
ДНЗ «Мукачівський професійний ліцей»
ТЕМА УРОКУ
„Тригонометрія-одна із найцікавіших розділів Алгебри”
(брейн-ринг)
Викладач математики
Петах В.Й.
Мукачево 2011 р.

гра
Брейн – ринг
Тема уроку:„Тригонометрія-одна із найцікавіших розділів Алгебри”
Мета:
- Узагальнити і систематизувати знання учнів проойденого матеріалу по темі «Тригонометрія»;
- Розвивати системність мислення, пам’ять, спостережливість, логічне мислення;
- Поглибити вміння аналізувати;
- Сприяти вихованню всебічно розвиненої особистості.
Комп’ютерна підтримка: MyTest, слайди.
Дидактичне забезпечення: комп’ютерна презентація основних етапів уроку, виконана в програмі Power Point, контрольно – діагностична система My Test, індивідуальні картки оцінювання знань учнів.
Методи та прийоми навчання: розв’язок кросворду, гра «Брейн –ринг», тестування, робота в малих групах.
План проведення:
(Змагаються між собою дві команди. Змагання проводиться в 3 тури)
- Перший тур-«Розв’язування кросворду»;
- Другий тур складається з 20 запитань, на які потрібно швидко і правильно відповісти.
- Третій тур-тестування на комп’ютерах і по карточках.
- Перегляд відео уроку.
- Підсумок уроку.
- Д/з.
Ведучий 1. Добрий день, дорогі друзі!
Брейн-ринг вітає вас!
Тема якого - „Тригонометрія-одна із найцікавіших розділів Алгебри”.
Ведучий 2. Я знаю, математика вас не лякає
І сни ночами не забирає,
А косинус лишень попереджає,
Ось синус вигнув свою спину,
Присвоїв альфу, як дитину,
А коло радіус шукає,
Який в клітинках десь блукає.
Ведучий 1. А сімка всіх питає:
«Таблицю множення без комп’ютера хтось знає?»
А двійка лебедем кружляє
І замість всіх відповідає:
«Любіть, кохайте, поважайте
І математику вивчайте.
Вона вам з часом знадобиться,
На екзаменах пригодиться!»
Ведучий 2. Сьогодні ви будете свідками найцікавішої боротьби між командами. В нашому змаганні не можна вигукувати з місця, тупотіти, свистіти. Категорично забороняється підказувати.
Ведучий 1. А зараз послухаємо склад команд. Отже, починаємо наш Брейн-ринг.
Виходять команди починається привітання.
Команда «Косинус». Команда «Косинус» радо вітає! Вболівайте за нас,
Бо розумні і красиві, ми –інтелектуали щасливі!
Ми, за справедливий і чесний конкурс,
в якому переможе сильніша команда і дружба.
Ми урочисто обіцяємо: якщо виграємо, то не задиратимемо носа, а якщо програємо – то не будемо лити гірких сліз.
Команда «Синус»: Щоб усе було гаразд.
Прикладемо старання .
Виконаємо дружно ми
Ведучих всі завдання.
Ми математику багато літ вивчаємо,
Тому багато дуже знаємо.
Хочемо, щоб противник наш.
Другом був завжди для нас.
(Дві команди сідають за столи. Починається гра).
Вчитель. Зараз ми з вами повторимо пройдений матеріал
Перший тур називається «Кросворд». Команда отримає 1 бал, якщо правильно відповість на нього. Якщо команда не правильно відповідає на питання, то право відповіді переходить до іншої команди. Першою починає та, капітан якої правильно відповість на моє питання.
Хто написав перший російський підручник з математики?
А. Лобачевський. С. Магницький.
В. Ковалевська. D. Колмогоров.
Ведучий.
Так, саме Леонтій Магницький у 1703 р. написав цей підручник і назвав його «Арифметика». Михайло Ломоносов називав цю книгу «вратами своєї вченості» і майже всю її знав напам'ять.
|
|
т |
а |
н |
г |
е |
н |
с |
о |
ї |
д |
а |
|||||
|
|
|
п |
а |
р |
н |
а |
|
|
|
|
||||||
|
|
с |
и |
н |
у |
с |
|
|
|
|
|
|
|||||
|
|
к |
о |
т |
а |
н |
г |
е |
н |
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
о |
с |
и |
н |
у |
с |
|
|
|
|
|
|
|
р |
а |
д |
і |
а |
н |
|
|
|
|
|
|
|
|
|
|
|
|
с |
и |
н |
у |
с |
о |
ї |
д |
а |
|
|
|
|
|
|
|
|
|
|
в |
і |
д |
є |
м |
н |
и |
й |
|
|
|
|
|
|
|
|
|
|
|
|
|
п |
е |
р |
і |
о |
д |
и |
ч |
н |
а |
|
|
|
|
|
|
|
|
|
т |
а |
н |
г |
е |
н |
с |
|
|
|
|
|
|
|
|
|
|
а |
р |
г |
у |
м |
е |
н |
т |
|
|
|
|
|
|
|
|
|
|
м |
і |
н |
у |
с |
|
|
|
|
|
|
|
|
ф |
у |
н |
к |
ц |
і |
я |
|
|
|
|
|
|
|
|
|
|
1.Назва графіка функції y=tgx.
2.Як називається функція y=f(x), якщо для будь-яких значень х та –х з області визначення виконується рівність f(-x)=f(x)?
3. Ордината точки Pα одиничного кола, в яку переходить початкова точка Р0(1;0) при повороті навколо центра кола на кут α рад.
4. Відношення абсциси х точки Pα(х;у) одиничного кола до ординати у.
5. Абсциса точки Pα одиничного кола, в яку переходить початкова точка Р0(1;0) при повороті навколо центра кола на кут α рад.
6. Центральний кут кола, якому відповідає довжина дуги, що дорівнює радіусу цього кола.
7.Назва графіка функції у=sinx.
8. Напрям обертального руху променя навколо своєї початкової точки О за годинниковою стрілкою.
9. Як називається функція у=f(x) з періодом Т≠ 0, якщо для будь-якого х
з області визначення f(x+T)=f(x-T)=f(x)?
10. Відношення ординати у точки Pα(х;у) одиничного кола до абсциси х.
11. Величина, від значень якої залежать значення функції.
12. Знак тригонометричної функції у=cosα в 2-ій та 3-ій координатних чвертях.
13. Залежність змінної у від змінної х, якщо кожному значенню х відповідає єдине значення у.
2. Другий тур «Хто більше?». Він складається з 20 запитань, на які потрібно швидко і правильно відповісти. Команда отримає 1 бал, якщо капітан команди першим підніме руку після того, як буде зачитано запитання і правильно відповість на нього.
У цьому турі мені потрібен асистент, який слідкуватиме за тим, хто з капітанів двох команд, які змагаються, першим підніме руку після того, як буде зачитано запитання.
Ведучий.
- Піфагор та його учні вважали, що «числа правлять світом». Розставте числа в порядку спадання.
А. Тисяча, В. Мільйон, С. Трильйон, D. Мільярд.
Відповідь. С, D, В, А.
Ведучий.
- Парна тригонометрична функція:
А. Косинус, В. Синус, С. Тангенс, D. Котангенс.
Ведучий.
- Проміжки зростання функції у=cosx:
А. [-![]() π + 2πn; 2πn], nєZ, С. [-π + 2πn; 2πn], nєZ,
π + 2πn; 2πn], nєZ, С. [-π + 2πn; 2πn], nєZ,
В. [-![]() π + πn; πn], nєZ. D. [-π + πn; πn], nєZ.
π + πn; πn], nєZ. D. [-π + πn; πn], nєZ.
Ведучий.
- Чому дорівнює cos30°?
А. ![]() , В. 1, С.
, В. 1, С. ![]() , D.
, D. ![]() .
.![]()
Ведучий.
- sin x > 0, якщо х є…
А. (π + 2πn; 2π+2πn), nєZ, В. [-π + 2πn; 2πn], nєZ,
С. [![]() π +2πn;
π +2πn; ![]() π+2πn], nєZ, D. ( 2πn; π + 2πn), nєZ,
π+2πn], nєZ, D. ( 2πn; π + 2πn), nєZ,
Ведучий.
- Чому дорівнює sin45°?
А. 1 , В. ![]() , С.
, С. ![]() , D.
, D. ![]() .
.![]()
Ведучий.
- Сформулювати основну тригонометричну тотожність.
![]() .
.
Ведучий.
- Проміжки спадання функції у=sinx:
А. [-π + 2πn; 2πn], nєZ, С. [-![]() π + 2πn;
π + 2πn; ![]() π +2πn], nєZ ,
π +2πn], nєZ ,
В. [![]() π +2πn;
π +2πn; ![]() π+2πn], nєZ, D. [2πn; π +2πn], nєZ..
π+2πn], nєZ, D. [2πn; π +2πn], nєZ..
Ведучий.
- Чому дорівнює сtg90°?
А. ![]() , В. 0, С. не існує, D.
, В. 0, С. не існує, D. ![]() .
.![]()
Ведучий.
- Проміжки спадання функції у=cosx:
А. [2πn; π +2πn], nєZ, С. [-![]() π + 2πn;
π + 2πn; ![]() π +2πn], nєZ ,
π +2πn], nєZ ,
В. [-![]() π +2πn;
π +2πn; ![]() π+2πn], nєZ. D. [-π + 2πn; 2πn], nєZ,
π+2πn], nєZ. D. [-π + 2πn; 2πn], nєZ,
Ведучий.
- Багато хто з математиків були філософами, геометрами, механіками, астрономами... Наприклад, Ісака Ньютона, видатного англійського вченого, математики вважають математиком, фізики — фізиком, астрономи — астрономом. Багато хто з математиків дружив зі спортом.
Хто з учених давнини був переможцем кулачних боїв?
А. Евклід. С. Піфагор.
В. Фалес. D. Архімед.
Ведучий.
Так, саме Піфагор брав участь у кулачному бою на олімпіаді в 548 р. до н.е. і довго утримував титул чемпіона в цьому виді спорту.
Ведучий.
- Відношення sinα до cosα становить…
Tgα
Ведучий.
- Чому дорівнює добуток tgα на ctgα?
1
Ведучий.
- Назвати екстремуми функції у=tgx.
Найбільшого та найменшого значень функція не має.
Ведучий.
- Графіком функції y=ctgx є...
А. Косинусоїда, В. Синусоїда
С. Тангенсоїда, D. Котангенсоїда.
Ведучий.
- Проміжки знакосталості функції у=ctgx.
ctgx>0 при xє(πn; ![]() π +πn), ctgx<0 при хє(-
π +πn), ctgx<0 при хє(-![]() π +πn; πn), nєZ.
π +πn; πn), nєZ.
Ведучий.
- Він ввів скорочені позначення тригонометричних функцій кута х: tg x, ctg x.
Ейлер Леонард
Ведучий. Використовуючи спеціально підібрану символіку, Ейлер полегшив мову математики, зробив її більш доступній для огляду і більш доступною. Він, наприклад, ввів скорочені позначення тригонометричних функцій кута х: tg x, ctg x, sec x, cosec x (позначення sin x і cos x: були введені І. Бернуллі).
Ведучий. Ейлер встановив сучасну точку зору на тригонометричні функції як функції числового аргументу. У працях Ейлера тригонометрія прийняла того вигляду, який вона має в даний час.
Ведучий.
- Що таке аргумент?
А. Музичний інструмент, В. Вісь Ох,
С. Незалежна змінна, D. Залежна змінна.
Ведучий.
Так, аргумент — це незалежна змінна. Поняття змінної величини ввів Рене Декарт у книзі «Геометрія» більш, ніж 300 років тому.
Ведучий.
- Алгебра тримається на чотирьох китах: число, рівняння, тотожність, функція. З прикладами функціональних залежностей людство зустрічалося з давніх-давен. А саме слово «функція» вперше застосував Готфрід Лейбніц у XVII ст. Воно походить від латинського “functio”.
Що в перекладі означає це слово?
А. Відновлення. С. Рух.
В. Виконання. D. Залежність.
Ведучий.
- Кого називають «батьком алгебри»?
А. Евкліда. В. Вієта. С. Декарта. D. Гаусса.
Ведучий. Так, це Франсуа Вієт, французький учений, за освітою юрист. Зацікавився астрономією, для цього йому були потрібні знання з алгебри і тригонометрії. Він почав вивчати математику, щоб написати великий астрономічний трактат. Та математика, як виявилося, ховала не менше загадок, ніж космос, їх вистачило на все життя. Трактат з астрономії не був написаний, а математика завдяки Вієту зробила великий крок у своєму розвитку. Вієта назвали «батьком алгебри».
Ведучий..Розповідають, що Вієт швидко розв'язав задачу, запропоновану голландським математиком ван-Роуменом як виклик математикам Європи. Було це так.
Ведучий. У жовтні 1594 р. король Франції Генріх IV приймав нідерландського посла. Зайшла мова про найвидатніших людей країни. Посол зауважив, що у Франції, мабуть, немає видатних математиків, бо, мовляв, ван-Роумен не назвав жодного француза. «Ви помиляєтесь,— відповів на це король.— У мене є математик, і досить видатний. Покличте Вієта».
Ведучий. Коли Франсуа з'явився, посол показав листа Роумена. Вієт прочитав його і тут же написав один з розв'язків рівняння, яке містилося у листі, а наступного дня надіслав ще 22 розв'язки, тобто знайшов усі додатні корені цього складного рівняння. Крім того, він виявив помилку в умові, що була допущена під час переписування, і виправив її. (Йшлося про розв'язування рівняння 45-го степеня з даними числовими коефіцієнтами, права частина якого дорівнює 0. Розв'язати так швидко це складне рівняння Вієту допомогли його знання з тригонометрії).
- Третій тур «Тестування».
Частина учнів проходять тестування на комп’ютерах за допомогою програмного засобу MyTest, отримуючи по закінченню відповідні бали, а інша-за індивідуальними карточками:
|
Варіант 1. |
Варіант 2. |
||||
|
Прізвище та ім’я |
|
Прізвище та ім’я |
|
||
|
1. Знайти cosα,
1) |
1. 2sin
1) |
||||
|
2. Знайти tgα, якщо sinα=
1) |
2. . Знайти cosα,
1) |
||||
|
3. Знайти ctgα, якщо sinα=
1) |
3. Знайти ctgα, якщо tgα=4
1) |
||||
|
4. 2sin
1) |
4. . Знайти tgα, якщо sinα=
1) |
||||
|
5. Знайти ctgα, якщо tgα=4
1) |
5. Знайти ctgα, якщо tgα=4
1) |
||||
|
Оцінка |
|
Оцінка |
|
||
- Перегляд відеоурока.(10 хв.)
- Підведення підсумку.(5 хв.)
Викладення оцінок за тести та Журі називає переможця.
6. Домашнє завдання:
-
Знайти sinα, cosα, ctgα, якщо tgα=
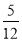 , π <α<
, π <α< 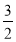 π .
π .
2. Повторити значення синусів, косинусів, тангенсів від 0 до 180![]()
Ведучий. Вітаємо всіх везунчиків з перемогою! Нехай і надалі вам щастить!
Підготувала:
Викладач математики та інформатики МПЛ ПЕТАХ В.Й.


про публікацію авторської розробки
Додати розробку
