Урок на тему: "Задачі на спосіб зведення до одиниці (другий вид). Порівняння виразів. Види трикутників. Складання і розв’язування рівнянь. Розв’язування складених задач."

Тема: Задачі на спосіб зведення до одиниці (другий вид). Порівняння виразів. Види трикутників. Складання і розв’язування рівнянь. Розв’язування складених задач.

Мета: Виробляти уміння розв’язувати задачі на спосіб зведення до одиниці.

Формувати вміння порівнювати вирази.

Вчити складати і розв’язувати рівняння.

Розвивати усне мовлення, уміння сформулювати і логічно оформити думку.

Виховувати охайність, старанність, доброзичливість.

Тип уроку: комбінований.

Обладнання: презентація, картки із самостійною роботою.

Хід уроку

I. Організація навчальної діяльності учнів

 (Перевіряю емоційну готовність учнів до уроку математики. Визначаю, чи є всі предмети, необхідні до уроку.)

- Доброго дня,  діти. Мене звати Ольга Олегівна. Сьогодні урок математики проведу у вас я. Тож, сідайте всі рівненько та приготуйтеся слухати.

ІІ. Каліграфічна хвилинка

•                   Відкрийте робочі зошити та запишіть число та класна робота.
•                   Цікавий факт: Мозок слонів - найбільший серед ссавців, його вага складає близько 5 кілограмів.

1.               Запишіть каліграфічно число, що вказує на вагу мозку слона. (5)
2.               Запишіть сусідів числа 5. (4,6)

3. Збільшіть кожне записане число на 60. (65, 64, 66)

4. Знайдіть і запишіть лише суму цифр числа 66. (6 + 6= 12)

Перевіряю записи чисел 5, 4, 6,65, 64, 66, 12  вибраних учнів. Звіряються зі слайдом.

– Встаньте ті, хто все виконав без помилок.

ІІІ. Усні обчислення

1. Колові приклади. (на слайд)

- Розв’язати кругові приклади усно. Кругові приклади розв’язуються дуже просто. Вони побудовані так, щоб результат першого був початком наступного, а результат останнього був початком першого. Погляньте на слайд.

2.               Обчисли приклади усно.

•                   Відкрийте підручники на с. 40. Знайдіть завдання 281. Розв’яжемо його усно.

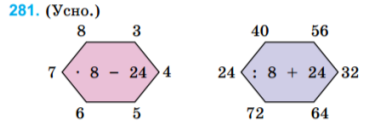
-  Розв’язуємо приклади по колу .

•                   Складіть перший вираз 7 ∙ 8 – 24.
•                   Знайдіть значення виразу.
•                   Складіть наступний вираз.

ІV. Актуалізація знань учнів

1.               Завдання 282.

•                   Знайдіть завдання 282.
•                   Що потрібно зробити? (Потрібно закінчити обчислення)
•                   Обчисліть та запишіть в зошит.
•                   Дайте відповіді на запитання.
•                   Що одержимо коли:

1.               Дільник множимо на частку? (Коли дільник множимо на частку одержимо ділене)
2.               Ділене ділимо на частку? (Коли ділене ділимо на частку одержимо дільник)

•                   Якщо а : b = с, то чому дорівнює b ∙ с? (b ∙ с дорівнює а)
•                   Чому дорівнює а : с? (а : с дорівнює b)

2. Робота з геометричним матеріалом.

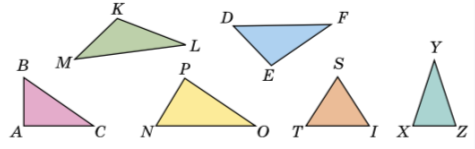
•                   Скільки всього трикутників? (Трикутників шість)
•                   Який трикутник називають прямокутним? (Прямокутний трикутник — це трикутник, один із кутів якого прямий)
•                   Назвіть їх. (Трикутник АСВ, NOP)
•                   Який трикутник називається гострокутний? (Гострокутний трикутник – це трикутник в якому всі кути менші за 90°.)
•                   Назвіть їх. (Трикутник ТSI, XZY)
•                   Який трикутник називають рівностороннім ? (Рівностороннім називають трикутник в якого всі сторони  мають однакову довжину.)
•                   Назвіть його. (Трикутник TSI)
•                   Який трикутник називається тупокутний? (Якщо один з кутів трикутника тупий, то його називають тупокутним трикутником)
•                   Назвіть їх. (Трикутник MKL, DFE)
•                   Який трикутник називають рівнобедреним? (Якщо дві сторони трикутника рівні, то його називають рівнобедреним.)
•                   Назвіть його. (Трикутник TSI, XZL)

V. Завдання уроку

- На сьогоднішньому уроці ви маєте:

•              Вчитись розв’язувати задачі на спосіб зведення до одиниці.
•              Вчитись розв’язувати рівняння.
•              Бути уважним і працьовитими.

VІ. Опрацювання нового матеріалу

1.              Розв’язування задачі 283 за таблицею.

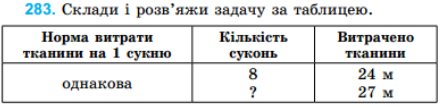
•                   Знайдіть задачу 283.
•                   Розгляньте таблицю.
•                   Назвіть трійку взаємопов’язаних величин? (Норма витрати тканини на 1 сукню, кількість суконь, витрачено тканини)
•                   Як знайти всього витрачено? (Потрібно норму помножити на кількість і одержимо витрачено)
•                   Як  можна визначити кількість? (Щоб визначити  кількість потрібно витрачено поділити нам норму)
•                   Як можна визначити норму? (Потрібно всього поділити на кількість)
•                   Що шили? (Шили сукні)
•                   Що відомо про пошиття суконь першого разу? (Відомо, що з 24 м тканини пошили 8 суконь)
•                   Що сказано про пошиття суконь другого разу? (Сказано, що на них витрачено 27 метрів тканини, а їх кількість не відома)
•                   Що треба знайти в задачі? (В задачі потрібно знайти скільки суконь пошили з 27 м тканини)
•                   Які дві величини потрібно знати, щоб дати відповідь на питання? (Потрібно знати такі величини як всього та норма)
•                   Чи обидві величини відомі? (Ні, всього відомо, а норма невідома) 
•                   Чи можемо знайти норму? (Можемо, потрібно всього поділити на кількість)
•                   Складіть текст до задачі. (З 24 м тканини пошили 8 суконь. Скільки суконь можна пошити з 27 м тканини.)
•                   Як знайти норму витрати? (Потрібно метри тканини, які витратили поділити на кількість суконь)
•                   Складіть дію. (24 м : 8 = 3 м)
•                   Як знайти яку кількість суконь пошили з 27 м тканини? (Потрібно всю витрачену тканину поділити на витрачену тканину на одну сукню)
•                   Складіть дію. (27 м : 3 м = 9 (с.))
•                   Запишіть в зошит.

Задача 283

1.               24 м : 8  = 3 м – норма витрати
2.               27 м : 3 м = 9 (с.)

Відповідь: 9 суконь можна пошити з 27 м тканини.

Фізкультхвилинка                                                                                                        Щоб ви трішки відпочили ми виконаємо фізкультхвилинку. Встаньте будь ласка. Вийдіть трішки із за парт і повторюйте рухи за мною.

Всі ми дружно працювали,

А тепер рівненько встали!

Руки вгору всі підняли,

Нахилились вліво, вправо.

Опустили руки вниз.

До сусіда посміхнулись,

Та й за парти повернулись.

1.               Розв’язування задачі 284.

•                   Прочитайте  задачу 284.
•                   Зачитай розв’язання.
•                   Складіть і розв’яжіть подібну задачу.
•                   Розкажіть задачу, яку склали.
•                   Наприклад: Невідоме число зменшили у 2 рази і дістали 8. Знайти невідоме число.

Розв’язання:

Позначимо невідоме число буквою х. Складемо рівняння: х : 2 = 8.

У цьому рівнянні невідоме число х є діленим. Знайдемо його.

х = 8 ∙ 2

х = 16

Відповідь: невідоме число дорівнює 16.

VІІ. Розвиток математичних знань і вмінь

1.              Розв’язування задачі 285.

•                   Прочитайте задачу.
•                   Скільки корові на день давали силосу? (Корові на день давали 24 кг силосу)
•                   Скільки силосу давали восьми вівцям на день? (Восьми вівцям на день давали силосу стільки ж скільки давали корові)
•                   Про що запитує задача? (На скільки кілограмів силосу більше давали на день корові, ніж вівці?)
•                   Які ключові слова в задачі? (Ключові слова в задачі корова і вівці)
•                   Складемо короткий запис. (слайд)

Корова – 24 кг силосу 

Вівця – 8 ов. – 24 кг, по ? кг

•                   Чи можемо відразу дати відповідь на запитання до задачі? (Ні, тому що спочатку потрібно дізнатися скільки силосу давали одній вівці на день)
•                   Як дізнатися скільки силосу давали одній вівці на день? (Потрібно кілограми силосу, які давали корові поділити на вівці)
•                   Складіть дію. (24 кг : 8 = 3 кг)
•                   Якою дією знайдемо відповідь на запитання до задачі? (Дією віднімання)
•                   Запишіть в зошит:

Задача 285

1.               24 кг : 8 = 3 кг – силосу давали одній вівці на день
2.               24 кг – 3 кг = 21 кг

Відповідь: на 21 кг силосу більше давали на день корові, ніж вівці.

1.               Розв’язування задачі 286.

•                   Прочитайте умову задачі.

5 м’ячів – залишиться 10 грн

8 м’ячів – не вистачить 14 грн

На різницю м’ячів треба 24 грн, тобто ціна 1 м’яча 8 грн.

Виділили 8 грн · 5 + 10 грн = 50 грн, або 8 грн · 8 – 14 грн = 50 грн

8. Самостійна робота

•                   А зараз ви виконайте невеличку самостійну роботу. Підпишіть картки. Прізвище та ім’я.

Варіант 1                                                     Варіант 2                                      ___________________________                     ______________________________

1.               х + 3 = 15                                                      1) х + 4 = 16
2.               х ∙ 5 = 25                                                       2) х ∙ 6 = 42
3.               х : 9 = 3                                                         3) х : 7 = 8

IX.  Підсумок уроку

- Якого типу задачі сьогодні розв’язували? (Ми розв’язували задачі на спосіб зведення до одиниці)
- Що викликало у вас труднощі?

Х. Домашнє завдання.

•                   Відкрийте ваші щоденники та запишіть с. 41 № 287, 288.
•                   На цьому наш урок завершений. Дякую за роботу. До побачення.