Урок "Натуральні числа. Число нуль. Цифри. Десятковий запис натуральних чисел"

Тема 2. Натуральні числа і дії з ними.

Геометричні фігури і величини. (52 години)

УРОК 4

Тема: Натуральні числа. Число нуль. Цифри. Десятковий запис натуральних чисел.

Мета:

навчальна:пригадати, як виконують дії з числами; сформувати поняття натурального числа і числа нуль, умін­ня розпізнавати натуральні числа, наводити їх приклади; навчитися застосовувати властивості дій над числами, для спрощення обчислень;

розвивальна: формувати вміння правильно і чітко висловлювати влас­ні думки, грамотно формулювати математичні твердження; сприяти формуванню пізнавального інтересу;

виховна: виховувати дисциплінованість, позитивне ставлення до знань.

Тип уроку: засвоєння знань, формування вмінь.

Хід уроку

I. Організаційний етап.

Перевірити готовність класу до уроку.

Налаштування на роботу.

II. Перевірка домашнього завдання.

Певірити наявність виконання аналізу діагностичної контрольної роботи, який був заданий, як домашня робота. Відповісти на запитання учнів.

III.  Формулювання мети і завдань уроку.

Про поняттям натурального числа учні ознайомлені з поперед­ніх класів, тому, по суті, йдеться про повторення матеріалу, розширення знань.

З метою формування пізнавального інтересу, позитивного став­лення до знань на цьому етапі уроку можна провести бесіду про іс­торію виникнення і розвитку поняття натурального числа.

Після цього повідомити учнів, що завдання цього уроку — уза­гальнити знання і досвід учнів щодо поняття натурального числа.

IV. Актуалізація опорних знань.

Оскільки тема не є новою для п’ятикласників, актуалізацію знань можна провести під час бесіди, в ході якої поставити перед учням такі завдання:

1. Прочитати числа:

1) 307 580;          2) 500 900;

3) 900 005;          4) 5 312 708 245.

2. Записати цифрами число: 4 тисячі 8 сотень 5 десятків.

V. Сприймання і засвоєння навчального матеріалу.

Багато тисяч років тому перед людьми вже виникала потреба рахувати членів родини, худобу, здобич на полюванні, рибу тощо. Уміння рахувати й обчислювати по трібні й зараз.

Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ..., які використовують під час лічби предметів, називають натуральними числами. Натуральні числа використовують також для визначення порядку розміщення предметів.

Числа, які ми використовуємо для лічби предметів, відповідають на запитання: скільки? (один, два, три...).

Числа, які ми використовуємо для визначення порядку розміщення предметів, відповідають на запитання: котрий ?(перший, другиу, третій).

Будь-яке натуральне число можна записати за допомогою десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Такий запис називають десятковим.

Усі натуральні числа, записані так, що за кожним числом іде наступне: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ..., утворюють натуральний ряд чисел.

Якщо натуральне число записане однією цифрою, то його називають одноцифровим, двома цифрами — двоцифровим тощо.

Натуральний ряд чисел має такі властивості:

1) має найменше число — 1;

2) кожне наступне число більше за попереднє на 1;

3) не має найбільшого числа. Хоч би яке велике число ми назвали, добавивши до нього 1, отримаємо ще більше число.

Щоб легше було читати натуральні числа, їх розбивають на групи справа наліво, по три цифри в кожній групі. Найперша група ліворуч може складатися з однієї, двох або трьох цифр. Наприклад 57 403.

Кожна група утворює класи: одиниць, тисяч, мільйонів і т. д. Кожний клас має три розряди: одиниць, десятків, сотень.

Якщо в числі відсутній якийсь розряд, то в запису числа на його місці стоїть цифра 0. Ця цифра служить також для запису числа «нуль». Це число означає «жодного». Якщо рахунок футбольного матчу 2 : 0, то це означає, що друга команда не забила жодного м’яча у ворота першої. Нуль не є натуральним числом.

Мільйон — це тисяча тисяч, його записують так: 1 000 000. Мільярд — це тисяча мільйонів, його записують так: 1 000 000 000.

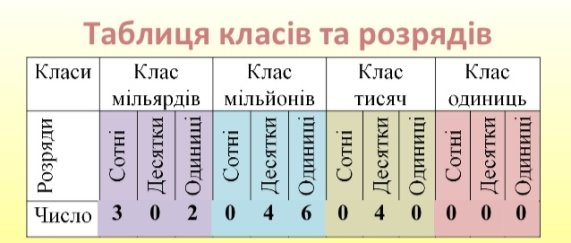
Приклад 1. Запиши цифрами число 37 мільйонів 142 тисячі 15.

Відповідь: 37 142 015.

Приклад 2. Запиши цифрами число тринадцять мільйонів дві тисячі.

Відповідь: 13 002 000.

У молодших класах уже подавали числа, менші від мільйона, у вигляді суми розрядних доданків. Таким самим чином можна подати будь-яке натуральне число. Наприклад,

7 213 049 = 7 000 000 + 200 000 + 10 000 + 3000 + 40 + 9.

Числа 7 000 000, 200 000, 10 000, 3000, 40, 9 у цьому прикладі є розрядними доданками.

Розглянуте число можна подати ще й так:

7 213 049 = 7 1 000 000 + 2 100 000 + 1 10 000 + 3 1000 + 4  10 +

+9 1.

Крім розрядних одиниць 1, 10, 100, 1000, 10 000 та 100 000, розглянутих раніше, також маємо 1 000 000, 10 000 000, 100 000 000 і т. д.

Давні римляни користувалися нумерацією, яка зберігається й нині під назвою римська нумерація. Ми використовуємо її для нумерації розділів книжки, циферблата на годиннику, для позначення століть тощо.

ДОДАТКОВИЙ МАТЕРІАЛ ДО УРОКУ

ІСТОРІЯ ВИНИКНЕННЯ НАТУРАЛЬНИХ ЧИСЕЛ

Поняття числа, яке видається нам простим і звичним, є абст­рактним поняттям, що могло утворитися тільки в результаті три­валої розумової роботи.

Першим кроком до виникнення лічби було встановлення від­повідності між предметами, які підлягають обчисленню, й деякою іншою сукупністю. Усім було відомо, що на небі Місяць один, ока у людини — два, пальців на руці — п’ять. Тому цими словами по­значали числа 1, 2, 5.

Очевидно, найзручніше було користуватися такою сукупніс­тю, до якої належали більш-менш однорідні предмети, наприклад пальці рук.

У більшості сучасних мов назви числівників утворені за десятко­вою системою, тобто за поданням чисел у вигляді суми числа одиниць (до 10), числа десятків (до 100), числа сотень (до 1000) тощо. Напри­клад, сімнадцять означає «сім на десять», сімдесят — «сім десятків». Безсумнівно, в основі цієї системи лежить лічба на пальцях.

Відомості про результати лічби спочатку зберігали за допомо­гою карбування на дереві чи костях або зав’язування вузликів на мотузках.

Звідки з’явилися наші арабські цифри 0, 1, 2, 3, 4, 5, 6, 7, 8, 9? Який народ винайшов нашу зручну десяткову позиційну систему числення? Арабські й перські підручники арифметики одноголосно приписують винахід дев’яти цифр індусам. Саме індуси створили ту систему, якою ми тепер користуємося. Усі основні арифметичні дії із цілими числами й дробами, в сучасному вигляді, зустрічаються в ін­дійських підручниках арифметики. Разом із правилами дій вони дій­шли до нас через арабів (тому ми і називаємо цифри арабськими).

Найважливішою цифрою є нуль. Це була геніальна ідея — зро­бити щось із нічого, дати цьому «щось» ім’я й винайти для нього символ. Винахід нуля приписують грецьким астрономам, які як нуль використовували знак «о».

Прийнята сьогодні в культурному світі арабська, або індуська, система числення на Русі з’явилася тільки в XVI або навіть XVII ст.

А що було до цього часу? Як наші предки позначали числа? Появу на Русі писемності й позначень для чисел відносять до періоду хрещен­ня, тобто до кінця X століття. Букви алфавіту одночасно були й чис­ловими знаками. Для того щоб підкреслити, що буква зображує чис­ло, над нею ставили особливу позначку — титло (~). Такий спосіб існував у багатьох давніх народів — греків, євреїв, фінікійців тощо.

VI. Формування вмінь.

Виконання вправ має сприяти закріпленню поняття нату­рального числа, ряду натуральних чисел.

Вправа 45. Прочитай числа:

1) 1 257 319;                    2) 32 000 517;

3) 1 213 592 731;     4) 102 015 007.

Вправа 47. Запиши цифрами числа:

1) 12 мільйонів 541 тисяча 301;                2) 105 мільйонів 13 тисяч 5;

3) 5 мільярдів 7 тисяч;  4) три мільйони дванадцять тисяч вісімнадцять;

5) одинадцять мільярдів сто десять мільйонів п’ять тисяч сорок два.

Вправа 54. Запиши числа у вигляді суми розрядних доданків:

1) 12 312 473;                  2) 5 010 980.

Вправа 56. Знайди число, яке записано у вигляді суми розрядних доданків:

1) 71 000 000 + 3 100 000 + 5 10 000 + 1 1 000 +  3 100 + 2 10 + 7;

2) 4 1 000 000 + 6 10 000 + 7 10 + 9;

3) 5 10 000 000 + 8 1000 + 3.

Вправа  57. Від числа 370 157 послідовно віднімай розрядні доданки й називай отримані числа доти, доки не одержиш 300 000:

370 157 - 7 = 370 150...

Вправа 58. Запиши число, яке:

1) на 5 менше від найменшого чотирицифрового числа;

2) на 3 більше за найбільше трицифрове число.

Вправа 59. Напиши трицифрове число, у якого цифра сотень у 3 рази більша за цифру десятків і на 4 менша від цифри одиниць.

Вправа 61. Запиши за допомогою римської нумерації число:

1) 15;         2) 17;          3) 23;               4) 48;             5) 52. 

Можливо, в класі будуть учні, які впораються із запропонова­ними вправами раніше за решту. Таким учням можна запропону­вати індивідуальні додаткові завдання підвищеної складності.

Картка № 1

Деяке натуральне число, більше за 4, позначили буквою . Запишіть для числа три попередніх і три наступних числа

Картка №2

Деяке натуральне число позначили буквою . Скільки чисел натураль­ного ряду міститься між числами і + 18?

VII. Підсумки уроку.

Фронтальна робота. Усне опитування:

1. Які числа називають натуральними?

2. Наведіть приклади чисел, що не є натуральними.

3. Назвіть найменше натуральне число.

4. Чи існує найбільше натуральне число?

5. Який запис називають рядом натуральних чисел?

6. Скільки натуральних чисел стоїть у натуральному ряду між числами 100 і 900?

VIII.Домашнє завдання

Повторіть теоретичний матеріал за параграфом 1 ст. 10-15 підручника.

Виконайте вправи.

Вправа 48. Запиши цифрами числа:

1) 2 мільйони 12 тисяч 501;

2) сто мільйонів п’ять.

Вправа 53. Запиши чотири рази поспіль число 27. Яке число утворилося? Скільки воно має мільйонів, тисяч, одиниць?

Вправа 55. Запиши число у вигляді суми розрядних доданків:

1) 7 321 548;                   2) 12 008 307.