Алгебра 9 клас 

Тема. Найпростіші перетворення графіків функцій.

Мета. Розвивати уміння учнів узагальнювати та систематизувати знання про квадратичну функцію, її властивості та графік. Формувати поняття найпростіших перетворень графіків  функцій через виконання конкретних завдань. Розвивати спостережливість, прийоми аналізу та синтезу. Виховувати соціальні компетенції: відповідального відношення до навчання, до необхідності використання джерел додаткової  літератури; уміння публічних виступів; почуття єдності команди. Тип уроку. Урок-практикум

Обладнання. Персональні комп’ютери із встановленим педагогічним програмним засобом (будь-який на розсуд вчителя), мультимедійний проектор, слайдові презентації про використання графіків в навколишньому світі, презентація „Кросворд”.

Хід уроку I.         Організація початку уроку (вітання з учнями)

Зверніть, будь ласка, увагу на три різнокольорові аркуші паперу, що приклеєні у вас біля монітора. Протягом уроку не забувайте про них, бо я хочу, щоб саме тут ви залишили свої враження від уроку. На зеленому аркуші напишіть про те, що ви дізналися на цьому уроці; на червоному – про що хочете дізнатися на наступних уроках, на жовтому – що вам на уроці особливо сподобалось.

           II.     Перевірка домашнього завдання та раніше засвоєних знань

1)    Перевірка письмового домашнього завдання біля дошки

2)    Розгадування кросворда (робота з класом)

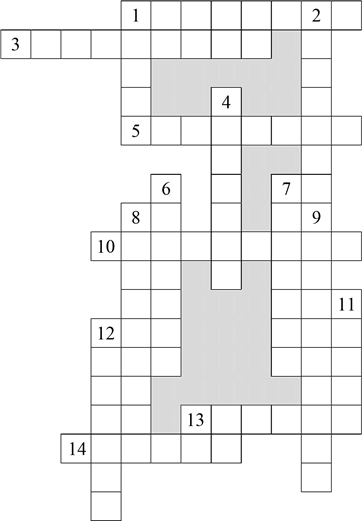
По горизонталі:

1.   Графік функції .

3.   Графік функції . 5.   Як називають незалежну змінну?

10. Один із способів задання функції.

13.    Функція, в якій більшому значенню аргумента відповідає менше значення функції.

14.    Множина точок координатної площини, абсциси яких дорівнюють усім значенням аргументу, а ординати – відповідним значенням функції. По вертикалі:

1.     Графік лінійної функції.

2.     Хто вперше в математиці використав слово функція?

4.  Як називають залежну змінну?

6.       Всі значення змінної у називають множиною…

7.       Функція, графіком якої є пряма лінія.

8.       Функція, в якій більшому значенню аргумента відповідає більше значення функції.

9.       Всі допустимі значення аргумента називають областю…

11.    Функція, графік якої симетричний відносно осі Оу.

12.    Функція, графік якої симетричний відносно точки початку координат.

         III.    Актуалізація опорних знань

Вибрані слайди з презентацій учнів, що були підготовлені до попередніх уроків демонструються при обговоренні питань:

1)    Дайте означення функції.

2)    Якими способами можна задати функцію?

3)    Що ми називаємо графіком функції?

4)    Які функції ви можете назвати?

5)    Які з даних рисунків є графіками яких-небудь функцій?

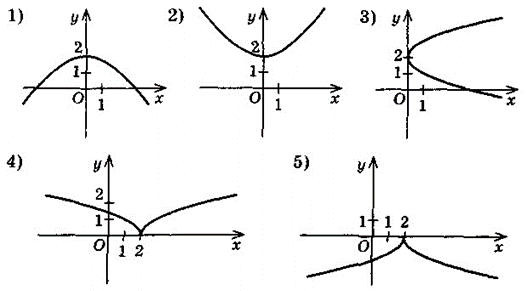
6)    Який графік має лінійна функція? Квадратична? Кубічна? Пряма пропорційність? Обернена пропорційність? Кореня квадратного?

7)    Коли функція є спадною? зростаючою?

8)    Коли функція є парною? непарною?

         IV.    Повідомлення теми та завдань уроку.

Сьогодні ми продовжимо вивчати функції. Зокрема дослідимо, що впливає на форму та розміщення графіка функції в системі координат. А також поміркуємо, чи допоможуть наші дослідження при побудові графіків функцій.

           V.     Вивчення нового матеріалу

1)    Робота з підручником

Учитель пропонує дітям розпочати опрацювання відповідного параграфа. Зазвичай підручник пропонує побудову графіків функцій графічним способом, який є досить громіздким. 

Після опрацювання двох-трьох абзаців робота зупиняється педагогом і переходить у подальше обговорення вищевказаних незручностей та підходів.

2)    Робота з програмним засобом 

Учителю слід нагадати особливості роботи з програмним засобом та символіку, яка буде використовуватись при роботі з GRAN-1.

Учні під керівництвом учителя перевіряють та налаштовують параметри вікна програмного засобу.

Далі учні працюють за інструкцією, яка відображається на екрані через мультимедійний проектор у вигляді слайдової презентації. Після кожного етапу роботи вчитель організовує обговорення та підведення підсумків.

а) Побудуємо графік функції . 

                                                          Аналогічно    будуються    графіки       функцій     та          

 (колір наступних графіків бажано змінювати). 

Учні роблять висновок за після відповіді на запитання:

•      Що змінилось при побудові графіків?

•      Чи змінилась форма параболи?..

Будуємо  графіки функцій  та  

Обговорення результатів побудови та формулювання правила: графік функції , де , можна одержати із графіка функції   за допомогою паралельного перенесення вздовж осі у на п одиниць угору; графік функції , де , можна одержати із графіка функції   за допомогою паралельного перенесення вздовж осі у на п одиниць униз.

б) Вилучення непотрібних для подальшої роботи графіків, залишивши тільки графік функції ,  

в) Побудуємо графіки функцій:

 , , . 

Обговорення результатів та формулювання правила: графік функції , де , можна одержати із графіка функції   за допомогою паралельного перенесення вздовж осі x на m одиниць ліворуч; графік функції

, де , можна одержати із графіка функції   за допомогою паралельного перенесення вздовж осі x на m одиниць праворуч. Питання до класу: 

 як будуть розміщені відносно точки початку системи координат графіки функцій ,  

                                                                         ,       ?

Учні обґрунтовують усно, а потім перевіряють побудовою, попередньо вилучивши всі графіки.

г) Самостійні дослідження учнів Досліджуємо графіки функцій: та ,

.

Результати обговорюємо та формулюємо правило: графік функції   можна одержати із графіка функції   за допомогою симетрії відносно осі х.

д) Досліджуємо графіки функцій: 

.

Результати обговорюємо та  формулюємо правило: графік

функції , де , можна одержати із графіка

функції   розтягнувши останній від осі Ох в а-разів, якщо , і стиснувши його до осі Ох в  разів, якщо

.

Про побудову графіків функцій з модулем учитель пропонує прочитати  вдома та розглянути на наступному уроці.

         VI.     Узагальнення та систематизація знань.

1)    Повторюються правила побудови графіків

2)    (Демонстрація учнівських презентацій)

Де зустрічається у природі, у побуті чи на виробництві графіки функцій? 

       VII.    Домашнє завдання

1)    Опрацювати відповідний параграф підручника, розв’язати  вибрані вправи середнього та достатнього рівнів.

2)    Дітям високого рівня навчальних досягнень підготувати презентацію побудови графіків функцій з модулем.

VIII.     Рефлексія  Підводяться підсумки уроку. 

Учні звертаються до зелених, а потім до жовтих аркушів біля своїх моніторів, ведуть бесіду з учителем та однокласниками. Обговорюють свої досягнення. Червоні ж аркуші прикріплюють до монітора учительського комп’ютера. Основні питання на них розглядають на наступному уроці.