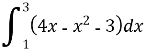урок: "Обчислення площ плоски хфігур за допомогою інтеграла"

Тема: Обчислення площі плоских фігур за допомогою інтеграла.

Мета:

Навчальна:  поглибити й розширити знання учнів про обчислення площі плоских фігур за допомогою визначеного  інтеграла;  закріпити навички знаходити визначений інтеграл; удосконалити вміння розв’язувати задачі ,що передбачають  обчислення площ плоских фігур за допомогою визначеного інтеграла;

Розвиваюча: розвивати спостережливість і логічне  мислення; продовжувати формувати та розвивати навички учнів розв’язувати математичні задачі;

Виховна: виховувати вміння раціонально використовувати   робочий час.

Тип уроку: закріплення знань та вмінь;

Обладнання: картки , інтерактивна дошка, комп’ютер, підручник . 

Домашня робота: Вправа 11.11(1-6);  дод. Тестові завдання «Перевір себе» ст. 67

 

Хід уроку

І. Організаційний момент (привітання)

ІІ. Формулювання теми та мети уроку. Мотивація

Доброго дня, дорогі одинадцятикласники та присутні! Дуже рада бачити вас на нашому уроці. Наше життя  - дуже цікаве, вона складається з різних моментів які ми можемо поділити на етапи, етап вашого народження, етап коли ви пішли до дитячого садочку , етап коли ви пішли до школи , і ось ви вже дорослі майбутні випускники.

 Серед усіх наук, що відкривають шлях до пізнання законів природи найвеличнішою, звичайно, є математика.  Опановувати новими математичними  знаннями  означає відкривати нові життєві істини.     

Основна ціль нашого уроку – розширити знання  про обчислення площі плоских фігур за допомогою визначеного  інтеграла;  закріпити навички знаходити визначений інтеграл; удосконалити вміння розв’язувати задачі ,що передбачають  обчислення площ плоских фігур за допомогою визначеного інтеграла 

Ключова ціль – впевнено себе почувати під час ЗНО де досить прості в розв’язанні задачі мають достатньо нестандартний зміст.

Пишемо сьогоднішнє число та тему: «Обчислення площ плоских фігур за допомогою інтеграла»

IV. Активізація опорних знань

Сьогоднішній урок ми побудуємо за етапами.    У вас на столі лежить лист оцінювання . Протягом уроку поетапно будете вписати зароблені бали, під кінець уроку підрахуйте та будете виставляти собі оцінку.

Етап перший

Знання збільшуються, а вміння вдосконалюються коли ними ділишся        Налаштовуємося на урок.

• З яким поняттям нерозривно пов’язане поняття визначеного інтеграла?

( Площа )

• Що таке первісна?

 ( Функція F(x) називається первісною функції f(x) на   деякому проміжку,  якщо для всіх х з цього проміжку   виконується рівість F̕(x)=f(x) )

• Назвіть формулу Ньютона-Лейбніца

                                               (  )

• Яка головна відмінність визначеного інтеграла від невизначеного?

                                       ( невизначений інтеграл-це функція, а визначений –це число)

• Як називається трапеція, площу якої ми знаходимо за допомогою визначеного інтеграла? (криволінійна)
• Як називається функція, яка стоїть під знаком інтеграла? (підінтегральна)
• Як називається множник dx у підінтегральному виразі?(диференціал)
• Як називається операція обернена до операції диференціювання?       (інтегрування)

Етап другий

Математику не можна вивчити, спостерігаючи як це робить сусід…

Згадаємо табличні інтеграли за допомогою гри «Простіше простого» з подальшою взаємоперевіркою . Учні розв’язують по варіантам , дається 2 хв. На розв’язування і 1хв на перевірку.( на роботу 3 хв)

Варіант 1	Варіант 2
1.	1.
B:	B: 1
2.	2.
B:1	B:
3.
B:	B:     B: -
4. dx	4.
B:	B:
5.dx	5.
B: 12	B:1

ІІІ. Застосування знань і вмінь

Етап третій

Не досить оволодіти премудрістю, потрібно також уміти користуватися нею

Розглянемо, де може знадобитись визначений інтеграл при розвязуванні задач з фізики. ( один учень працює біля дошки, решта в зошитах) ( на виконання-3 хв ) Задача

Раз мова зайшла про електроенергію, то хотілося б сказати, що Сила струму в провіднику з часом змінюється за законом . Яка кількість електрики пройде через поперечний переріз провідника за час від третьої до шостої секунди?

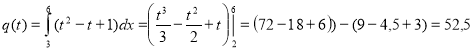(Кл)

 Етап четвертий

Щоб кожен міг з упевненістю сказати, що він досяг успіху, необхідно самостійно працювати. Адже мудрість проголошує…  Покажи мені - і я запам’ятаю. Дай мені діяти самому - і  я навчусь.

Робота в парах  з подальшою самоперевіркою  (робота с картками)

Виконання  завдань на встановлення відповідності

Установіть відповідність  між заданою фігурою (1-4) та формулою для обчислення її площі (А-Д)

1	Фігура, обмежена параболою y=x(x-4) і прямою  y=-3	А
2	Фігура, обмежена параболою y=x2-4x+3  і прямою  y=3	Б
3	Фігура, обмежена параболою y=x2-4x+3  і прямою  y=8	В
4	Фігура, обмежена параболою y=x(x-4) і прямими  y=0, x=5	Г
		Д

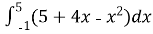1. y=x(x-4)               1- Д

      y= -3 

2) y=x²-4x+3                      2- А

    y=3

3)y=x²-4x+3               3- Г

 y=8

     4) y=x(x-4)                 4- В

         y=0

 

 Етап п’ятий

Сміливість розуму характерна для всіх математиків. Математик не любить, коли йому про щось розповідають, він сам хоче дійти до всього.

Робота з підручником №11.10 (по одному учню працюють біля дошки)

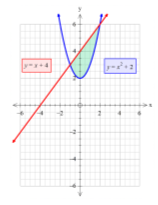8)y=;    y=x+4;

= x+4

x -4=0

=0

D=3

X₁=2;  x₂=-1

=

S=4,5

 

13) y=      x+y=8   (y=8-x)

  = 8-x    7-8x

D= 6

x₁=1      x₂=7

 

 

    

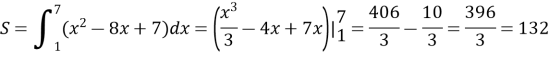
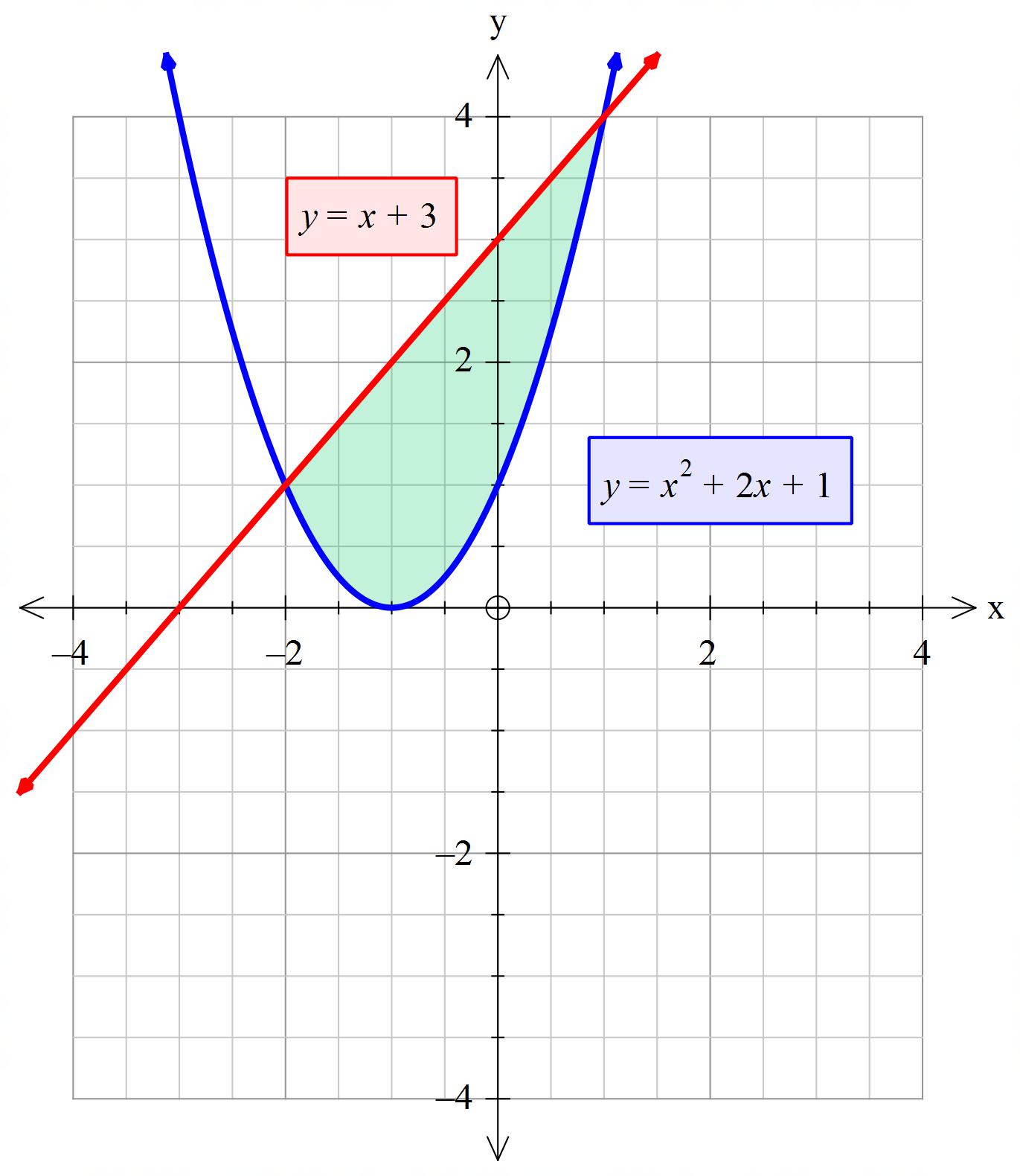
Задача 1: За рисунком визначити межі інтегрування і обчислити площу.

 

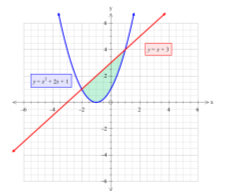
y=

y=+3

x=1

x=-2

+3

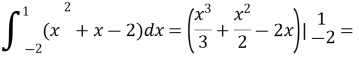
= -4,5         

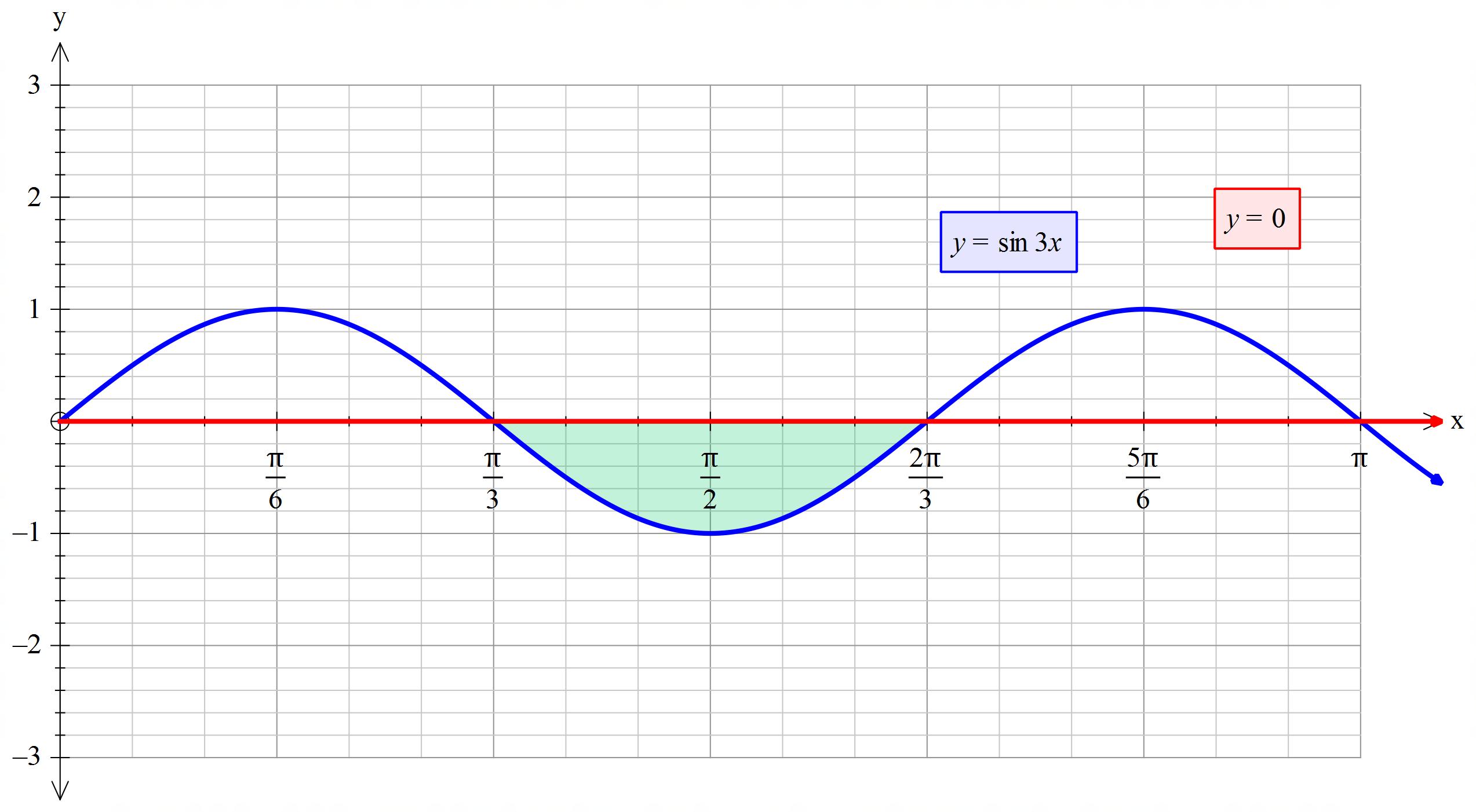
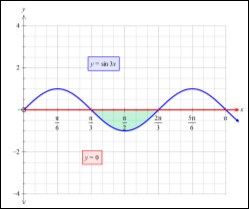Задача 2:

y=sin3x

y=0

x=

x=

=

=-

 

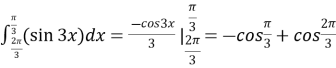S=1

Додатково

Площа фігури, обмеженої графіком функції у=2х+1, прямими х=2,   х=а  і  у=0,   дорівнює 4. Обчисліть а.

Підсумок уроку

Наш урок добігає кінця. Наступний  етап для вас це здача ЗНО , бажаю вам успіху. А закінчити урок я хочу такими словами.

Усе людське життя - це не що інше, як постійне визначення мети та бажання досягти успіху під час розв’язування все нових задач та проблем. Учіть свій розум та душу бачити добро, бачити цікаве у звичайних математичних виразах  і тоді дорога до успіху буде для вас відкрита. Дякую вам за урок. Бажаю всім успіхів і гарного настрою! Шановні одинадцятикласники , здайте мені листи для оцінювання.

Домашня робота

Вправа11.6  (3) ;  11.11(1-6);  дод. Тестові завдання «Перевір себе» ст. 67