Урок "Обернені тригонометричні функції"

ТЕМА УРОКУ

Поняття про обернену функцію. Обернені тригонометричні функції, їх властивості та побудова

МЕТА УРОКУ

 

Дидактична:

• Ознайомити учнів з поняттям «обернена функція», розглянути вигляд  та розкрити властивості обернених тригонометричних функцій.

Розвиваюча:

• розвивати аналітичне мислення.

 

ТИП УРОКУ

Засвоєння нових знань.

 

ПЛАН УРОКУ

 

1. Організаційна частина.
2. Перевірка Д/з. Актуалізація опорних знань.
3. Повідомлення нового матеріалу.
4. Засвоєння нового матеріалу.
5. Підсумки. Домашнє завдання.

 

ХІД УРОКУ

 

І.     Вітаюся. Відмічаю відсутніх.

ІІ.  Фронтальне опитування:

 Тригонометричні функції та їх властивості.    

ІІІ. 1. Поняття оберненої функції

 Функція f, яка має обернену, називається оборотною.

 Оберненою до даної оборотної функції називається така функція , яка кожному із множини значень функції ставить у відповідність єдине число х із її області визначення.

 Графік функції , оберненої до функції , симетричний графіку відносно прямої .

Алгоритм знаходження оберненої функції:

1. З’ясовуємо, чи є функція оборотною на всій області визначення. Якщо ні, то виділяємо підмножину області визначення, де існує функція обернена до .
2. Розв’язуємо рівняння відносно змінної х, тобто знаходимо функцію 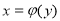, яка є оберненою до .
3. Міняємо позначення змінних  .

 

2.Функція обернена до .

 Розглянемо на проміжку функція монотонна.

 Відобразимо отриманий графік відносно .

Властивості:

1.

2.

3. непарна, 

4. неперіодична

5. зростаюча

6.

 

 Арксинусом числа а називається такий кут х, синус якого дорівнює а.

        

3. Функція обернена до .

Розглянемо  на проміжку функція монотонна.

 Відобразимо отриманий графік відносно .

Властивості:

1.

2.

3. не є парна, не є непарна 

4. неперіодична

5. спадаюча

6.

 

4. Функція обернена до .

Властивості:

1.

2.

3. непарна, 

4. неперіодична

5. зростаюча

6.

 

 

 

 

 

 

5. Функція обернена до .

 

Властивості:

1.

2.

3. не є парна, не є непарна 

4. неперіодична

5. спадаюча

6.

 

 

 

 

ІV. Обчислити:

    1) так як  .

    2)

   3)

   4)

    5)

    6)

    7)

    8)

   9)

V.  Д/з Шкіль ст.. 125  №  12(1-10).