Бібрська  опорний ліцей імені Уляни  Кравченко

 

 

 

 

 

Цікава,  могутня  і  вічна  теорема  Піфагора

 

 

 

 

 

 

 

Вчитель математики

 Бібрського опорного ліцею  імені Уляни Кравченко Боднар  Г.Я.

               

Зміст

 

1.                  Вступ

2.                  Історичні   відомості про життя та діяльність Піфагора

3.                  Теорема Піфагора  та її доведення   різними  способами

4.                  Старовинні задачі на використання теореми Піфагора 

5.                  Важливі відкриття Піфагора та його школи  

6.                  Кросворди 

7.                  Поетична сторінка 

8.                  Цікаво знати 

9.                  Використана  література

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.Вступ

 

  Теорема  Піфагора  -  одна  з  основних  в  евклідовій  геометрії.  Відомий  вчений Іоганн  Кеплер  назвав  її  одним  із  скарбів  геометрії,  що  можна  порівняти    з  мірою  золота. 

       Причинами такої популярності є простота, краса  та   значення  теореми. Справді, теорема Піфагора проста, але не очевидна. Це поєднання двох суперечностей і надає їй особливої привабливості. Окрім цього, теорема Піфагора має велике значення: вона використовується на кожному кроці, той факт, що існує близько 150 різних доведень цієї теореми доводить велику кількість її реальних реалізацій.

   Завдяки  їй  можна  більшість  теорем  геометрії  та  розв’язати  не  одну  задачу. Тому  її  потрібно  добре  засвоїти.    Це  і  стало  основною   метою  проекту   ,, Цікава,  могутня  і  вічна  теорема  Піфагора”. Результатом  роботи  над  проектом  став довідник  для  школярів  під  однойменною  назвою. 

   У  даному  довіднику   зібрані  цікаві  дані  з  життя  і  діяльності    Піфагора  та  його   школи,  відомості  про  найважливіші  їхні  відкриття,  подано  декілька  доведень  теореми  та   старовинні  задачі  на  її  використання,   запропоновано  кросворди  та  поетичну  сторінку,  присвячену   творцю  теореми. 

     Як  не  старіють  твори  мистецтва  і  живуть  вічно,  так  і  мудрість,  подарована  людству  такими  мислителями,  яким  був  Піфагор,  назавжди   залишиться  з  нами.   

 

 

 

 

 

 

 

Геометрія володіє двома скарбами:

теоремою Піфагора і «золотим перерізом» Іоганн Кеплер

 

2.             Історичні відомості про  життя  та         діяльність  Піфагора

 

                       Легенда про народження    

                                                                             

  Піфагор жив у 6 столітті до нашої ери. Він народився  Греції, на   острові Самос у сім’ї  золотих  справ майстра    Мнесарха.         

     За легендою оракул пророчив йому та його дружині Парфенісі народження сина, який буде славитися віками своєю мудрістю, справами та красою. Пророцтво збулося, і  тоді Парфеніса приймає ім’я Піфіада, на честь Аполлона Піфійського, а сина називає Піфагором, на честь пророцтва Піфії. У легенді нічого не сказано про рік народження Піфагора, історичні дослідження датують його появу на світ приблизно 580 роком до нашої ери. 

 

Дитячі та юнацькі роки

 

Можливості дати сину гарну освіту та виховання у Мнесарха були. Як і будь-який батько, Мнесарх мріяв, що син буде продовжувати його справу - ремесло золотих справ майстра. Життя вирішило інакше. Майбутній математик та філософ вже в дитинстві виявив велику здатність до наук. У свого першого вчителя Гермодамаса Піфагор отримав знання основ музики та живопису. Для покращення пам’яті Гермодамас примушував його вчити пісні з «Іліади» та «Одіссеї». Перший вчитель навчив Піфагора любити природу та вивчати її таємниці.

           Пройшло кілька років, і за порадою свого вчителя Піфагор вирішує продовжити навчання в Єгипті, у жерців. Потрапити до Єгипту у той час було дуже важко, тому що країну практично закрили для греків. За допомогою вчителя Піфагору вдається залишити острів Самос. Але до Єгипту далеко, і Піфагор поки що живе на острові Лесбос. Там відбувається знайомство Піфагора з філософом Ферекідом – другом Фалеса. У Ферекіда Піфагор навчається астрології, таємницям чисел, медицині та іншим обов’язковим, на той час, наукам.  Піфагор прожив на Лесбосі кілька років. Звідти шлях Піфагора лежить у Мілет до відомого Фалеса,

засновника першої в історії філософської школи.   Фалесу  на  той  час  уже  йшов  восьмий  десяток.  За  його  порадою   Піфагор  вирушає  до  Єгипту.      Навчання Піфагора в Єгипті сприяє тому, що він стає одним із найбільш освічених людей свого часу. Пробувши  тут   близько  20  років  і  добре  засвоївши    всі  науки  єгиптян,  в  тому  числі  і  математику,    він    переїзджає  у  Вавилон,  де  ознайомлюється  із   науковими  знаннями  жерців.  І тільки в 60 років Піфагору вдалося повернутися на Батьківщину.

 

Піфагорійська школа

Після повернення додому Піфагор  переселився  до Південної Італії,  яку  тоді називали великою Грецією.     Тут, на острові  Сицилія в Кротоні,у нього народжується власна філософська

школа,яка  діяла  майже  30  років  і  здобула  велику  популярність,  головним  чином  досягненнями  у  галузі  математики  та  астрономії..  Це був одночасно і релігійний союз, і політичний клуб, і наукове товариство. Учні цієї школи зобов’язувались вести так     званий піфагорійський спосіб життя. Статут піфагорійського союзу був дуже суворим. Кожний, хто вступав до нього, відмовлявся від особисто власності на користь союзу, зобов’язувався не проливати  крові, не вживати м’ясної їжі, берегти   таємницю вчення  свого вчителя. Членам школи  заборонялося навчати інших за винагороду. Всі учні  Піфагора і він сам були працелюбні.

Усе впорядковується відносно чисел

  

 Піфагорійці вважали, що всі тіла  складаються   найменших частинок, «одиниць буття», які в різних сполученнях відповідають різним геометричним фігурам. Число для Піфагора було і матерією, і формою всього світу. З цього уявлення виходила і основна теза піфагорійців: ,, Початком  усього  є  числа,  які  керують  світом”.  Тому пояснювати природні явища потрібно лише з їхньою допомогою. Отже,  той,  хто  хоче  пізнати  всі  речі,  повинен  зрозуміти  природу  числа  і  гармонію  чисел.   

     Особливе  значення  піфагорійці  надавали  першим  чотирьом  парним  і  непарним  натуральним  числам.  Їхня  сума  ( 1+ 3 + 5 +7 ) +  ( 2 + 4 + 6 + 8 ) =36.  Крім  цього  число  36 – це  сума  кубів   перших  трьох  натуральних  чисел:  36=1³+2³+3³.   Тому  найстрашнішою  клятвою  у  школі  Піфагора  вважалась  клятва  числом  36.

   Числам надавали містичних властивостей. Одні числа приносять добро, інші зло, успіх тощо. Піфагор вважав, що душа – теж число, вона безсмертна і передається від однієї людини до іншої. Сучасна церква признає числову містику. Так, у Біблії число 666 є число звіра, 12 несе щастя, а 13 – нещастя. Піфагор вважав, що число 5 символізує колір, 6 – холод, 7 – розум, здоров’я та світло, 8 – кохання та дружбу, 9 – постійність. Особливо ненависними піфагорійцям були числа 13 та 17.

Піфагор  та  його  учнів  зробили  багато  нових  відкриттів   у  математиці  та  астрономії.  Прожив  відомий  учений  за   легендами  довге  життя  і  загинув  в  одній  з  сутичок  під  час  народного  повстання  у Греції    у  віці  майже  90  років.

Філософське вчення Піфагора.

Дослідження   піфагорійців  у  музиці

 

Піфагор навчав медицині, принципам політичної  діяльності,астрономії, математиці, музиці, етиці.  З його школи вийшли відомі політичні та державні діячі, історики, математики та астрономи. Це був не лише  вчитель, але й дослідник.

    Дослідниками ставали і його  учні. У школі Піфагора вперше був виказаний здогад щодо кулястості Землі. 

     Гармонія  у  піфагорійців  була  поняттям  широким.   Вони  її  шукали  не  тільки  у  геометрії,  арифметиці,  у  рухах  небесних  тіл,   але  і  в  музиці.                                                  

     Піфагор розвивав теорію музики й акустики,  створив відому «піфагорійську гаму». Учні  Піфагора  дійшли  висновку,  що  якісні  відмінності  звуків  обумовлюються  кількісними   розходженнями  довжин  струн.  Наприклад, відношення  числа  коливань  у  чистої  квінти  2:3,       у  кварти  3:4,  октави  1:2.  Гармонійний  акорд  виходить  при  звучанні  трьох  струн,  коли  їхні  довжини  зіставляються  зі  співвідношенням  чисел  3:4:6.  Тому  Піфагорові  приписують  створення  математичної  теорії  музики.  Крім  цього,  за  легендами,  сам  він  непогано  грав  на  арфі.         Особливе  місце  в    доктрині   піфагореїзму   займало  вчення про  душу  і належне  поводження    людини. Піфагор  виділяв   три  складові   людської  душі:  судження, розум  і пристрасті.  Душа   вічна   розумом,   а   інші  її   частини          ( судження  і пристрасті)  є   загальними  для  людей і  тварин.  Піфагор   заснував релігію,  яка  помітно    відрізняється  від  тодішньої  грецької  традиції.    Його  вчення про  безсмертя  душі   будувалося   на принципах  повної   підпорядкованості   богам.

   Релігійне і моральне  в  поглядах  Піфагора часто  збігається.  Досконало володіючи методами єгипетських жерців, Піфагор  «очищував душі своїх слухачів, виганяв вади з серця  та наповнював уми світлою правдою». В «Золотих  віршах» Піфагор показав ті моральні правила, суворе   виконання яких призводить до ідеалу.

  

Золоті  вірші  ( Поради  Піфагора)

                Живи з людьми так, щоб твої друзі не стали недругами, а недруги стали друзями.

                       Твори  велике,  не  обіцяючи  великого. 

                                     Не  роби  ніколи  того,  чого  не  знаєш.  Але  

навчися  усього, що  варто   знати,  і  тоді  будеш  вести  спокійне  життя.

                Не  роби  нічого  ганебного    ні  в  присутності  інших,  ні  таємно.  Першим  твоїм  законом  має  бути  повага  до  себе  самого.

                Лише  неблагородна  людина  здатна  в  очі  хвалити,  а  поза  очі  лихословити. 

                Не  давай  дурневі  в  руки  меч,  а  нечесним  -  владу.

                Не нехтуй здоров’ям свого тіла. Доставляй   йому  вчасно  їжу  і  питво,  і  вправи,  без  яких  воно  бідує.

                       Привчайся жити просто і без розкошів.

 Не заплющуй  очей тоді, коли хочеш спати, не проаналізувавши  всіх своїх вчинків за минулий день.  Усе  впорядковується  відповідно  до  чисел. 

                   

   На перстені Піфагора було викарбувано такий девіз:  ,,Тимчасова невдача краща тимчасової удачі ”.  

     У якості символа піфагорійці вибрали  пентаграму –  п’ятикутну зірку.    Це символ здоров’я  і досконалості,  опізнавальний знак піфагорійців.

                                                                           

3.  Теорема  Піфагора  та  її  доведення  різними  способами

 Добре  засвоєна  мудрість   не  забувається  ніколи

Піфагор

 

Теорема  Піфагора.   У  прямокутному  трикутнику  квадрат  гіпотенузи  дорівнює  сумі  квадратів  його  катетів. 

  

 

 

 

Формулювання  теореми  за  часів  Піфагора.

 

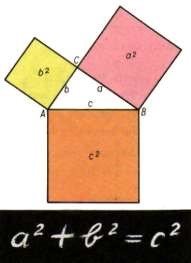               Площа  квадрата,  побудованого  на  гіпотенузі   прямокутного  трикутника 

дорівнює                сумі                 площ               квадратів   побудованих         на            катетах           цього  трикутника.

 

 

 

 

 

 

 

           Існує  дуже    багато  доведень  цієї  теореми     (  понад 150 різних). Пропонуємо деякі з них.  

                       1.  Доведення  під девізом   ,, Дивись!"

 

 

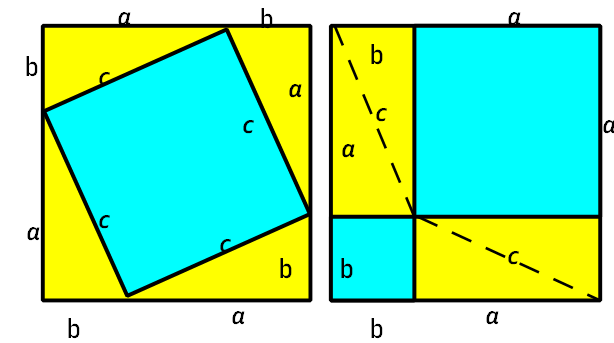
Доведення

 

На  малюнках  зображено  два  рівних  квадрати  зі  стороною  а + b.  Кожний  квадрат  розбито  на  частини,  які  складаються  з  квадратів  і  прямокутних  трикутників.  У  першому  випадку,  якщо  від  площі    квадрата  відняти  площі   чотирьох  рівних  прямокутних  трикутників з  катетами  а  та  b, то  отримаємо  площу  заштрихованого  квадрата  зі  стороною  с.  У  другому  випадку,  якщо  від  площі   такого  ж   квадрата  відняти  площі   чотирьох  рівних  прямокутних  трикутників,(  які  дорівнюють  попереднім  за  двома  катетами ), то  площа  двох    квадратів  дорівнюватиме  а²  та  b². 

Оскільки  від  рівних  площ  великих  квадратів  відняли   рівні  площі  прямокутних  трикутників,   то  залишаються  рівні  величини:   с² = а² + b^{2 .}

Це  доведення  використали  ще  у  стародавній  Індії.  А  саме,  доведення  полягає  в  одному  слові  - дивись!

2.      Доведення  із використанням  теми  ,,Подібність  трикутників"

 

                     С                       Доведення

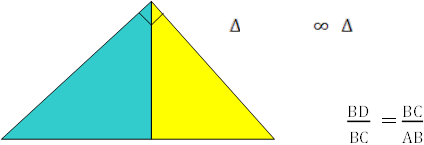
                                     АВС      АСD.   Тоді:   .                    

                                                 Звідси   АС² = АВ∙АD.   (1)

                                                 Аналогічно  АВС      СВD.               

                                              Тоді:                 і  ВC² = АВ∙ВD.  (2)

А                    D                   B     Додавши    рівності (1)   та  (2),

отримаємо:    АС² +  ВС² = АВ∙АD + АВ∙ВD=АВ∙( АD + ВD )= = АВ∙АВ = АВ².      Отже,  АВ² = АС²  +  ВС²,  що  і  потрібно  було  довести.

 

3.      Доведення  із  використанням  тригонометричних  понять

                       С

                                Оскільки  ,    то  

                                              АС² = АВ∙АD. (1)

                                             і   ВC² = АВ∙ВD.  (2)  

А                      D            B        Додавши    рівності (1)   та  (2),

отримаємо:     АС² +  ВС² = АВ∙АD + АВ∙ВD =АВ∙( АD + ВD ) = АВ∙АВ = АВ².             Отже,  АВ² = АС²  + ВС²,  що  і  потрібно  було  довести.

 

4.      Доведення теореми  з  використанням  основної тригонометричної  тотожності      𝐬𝐢𝐧^𝟐 𝜶 + 𝐜𝐨𝐬^𝟐 𝜶 = 𝟏

А

     𝛼                                             Доведення

                             Нехай  < А = α. Тоді   .           

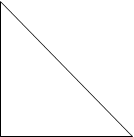                                     Оскільки    sin² 𝛼 + cos² 𝛼 = 1,

 С                       В     то = 1    і     ВС² + АС² = АВ²,           що  й   потрібно було довести.

5.      Доведення   з   використання  теми:  ,, Властивість  січної  та  дотичної,  проведених  до кола  з  однієї  точки ”

 

 

   К                                                           Доведення                                 

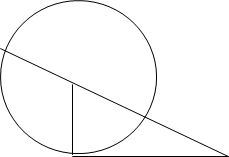           В                                                                                                                         D                         

      

          

         С                       А

                         Будуємо  коло  з  центром  в  точці    В  і  радіусом  ВС.  Воно  перетне  гіпотенузу  АВ  в  точці  D.  Оскільки  ВС ┴ АС,  де  ВС  -  радіус,  то  це  означає,  що  АС -  дотична  до  кола.  Пряма  АК  є  січною  і  перетинає  коло  в  точках  D  і  К.   За  властивістю  січної  та  дотичної,  проведених  до  кола з  однієї  точки  маємо:  АС² =АК∙АD  (1) Оскільки АК = АВ + ВК = AB +  BC,  AD=AB – BD=AB – BC. Підставивши  ці  вирази  у  формулу  (1)  отримаємо: 

АС² = ( АВ + ВС )∙( АВ – ВС ) = АВ² – ВС².   Звідси          АВ² = АС²  +  ВС² ,що  і  потрібно  було  довести.

  Це  доведення  цікаве  тим,  що  іноді  допоміжні  побудови  допомагають  отримати  бажаний  результат.  

 

6. Доведення  теореми   з  використанням  декартових  координат

 

   Введемо  систему координат:   катети  трикутника  лежать  на осях,  початок  координат  у вершині прямого                                        У                                        Тоді   А(а;о),    В(b;0),    С(0;0). 

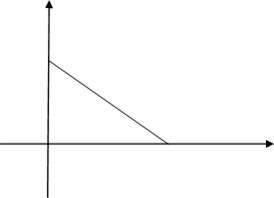 В (0; b)                           Знайдемо   відстані   АВ,  АС,   ВС,                                                           використавши формулу  для                                                                  обчислення  відстані   між  точками:                                                             d² = (х₂- х₁)² + (у₂- у₁)²,  де  d -             

С(0;0)             А(а:0)        Х     відстань  між  точками 

                                                  А(х₁; у₁)   і   В(х₂; у₂).

АВ²=( 0–а)² + (b – 0)²   = а²  + b²,  АС² = (0 - а)² + ( 0 – 0)² = а²,    ВС² = (0 – 0)² + ( 0 – b)² = b². Звідси,   АВ² = АС² + ВС²,  що  і  потрібно  довести.

                                      

                                  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4.              Старовинні задачі на використання теореми Піфагора

Задача  1  

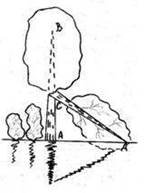Одинока тополя на березі річки росла Та поривом вітру зламана була .

 Упала верхів’ям до краю  ріки.

3 фути лишилося від стовбура тільки А річки в тім місці шириною у 4 фути була  Яка висота тополі  бути  могла?

 

Розв’язування

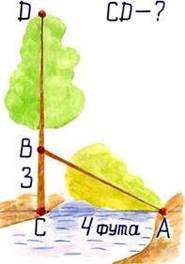Нехай СD -висота тополі СB = 3 фути -  висота стовбура, що залишився після злому  вітром,   АС =4 фути-ширина річки.  Тоді, ∆ АВС – єгипетський і АВ його гіпотенуза довжиною 5футів.        

Отже,  висота   тополі  СD = ВD + ВС= АВ + ВС = 5+3=8 (футів ). Відповідь:  8 футів. 

 

 

Задача  2  

Дві вежі  одна з яких заввишки 40 футів, а друга 30футів,  розташовані на відстані 50 футів одна від одної. До криниці,  що знаходиться  між ними одночасно з обох веж злетіло по пташині.  Рухаючись з однаковою швидкістю, вони прилетіли до криниці одночасно. Знайти відстань від криниці до найближчої вежі ( у футах ) 

Розв’язування

   А     

                                                 В

40ф.

                                                 30ф. 

     С    х      К       50 –х          D

 

   Нехай АС-вежа довжиною 40 футів, ВD - вежа довжиною 30 футів,  К- криниця, що знаходиться  між вежами.  Нехай відстань  від  першої вежі до криниці СК=х  футів,  а відстань до другої вежі від криниці КD = (50 – х)футів. Оскільки,  пташки,  що летіли з обох веж  прилетіли до криниці одночасно,  то  АК = ВК.   

     За теоремою Піфагора  АК² =АС² + СК² =40² + х²=1600 + х², 

ВК² = ВD ² + КD ² =30² + (50 –  х)² = 900 + (2500 –  100х + х²) = 

= 900 +2500 – 100х + х² = 3 400 – 100+х²; Отже,   1600 + х² =3400 – 100х + х²; 

        100х =3400 – 1500; 

         100х=1800;    х=18 (футів). 

Отже , відстань від криниці до найближчої вежі 18футів.   Відповідь;  18 футів. 

 

Задача  3  

Над деревом тихим висотою з пів фута   Піднімалися лотоса квітка. 

Яка росла одиноко.

Та вітер з сильним поривом відніс її в бік.

І не стало видно квітки над водою. 

Знайшов її рибалка ранньою весною. 

В двох футах від місця де вона росла. 

 І так пропонуємо вам запитання:

Яка в цьому  місці  води глибина? 

А                                   Розв’язування

    

   С         2      В                                 

        х              х+  

 

         

   D

     

Нехай СD = х футів  - глибина озера  СВ=2 фути – відстань,  на яку відніс вітер лотос      ВD =  АD = (х +  ) фути 

Отже ,

      ВD²=ВС² + СD²;                         

      ;

        х = 4 + х²;        х = 4 –  ¹;

4   х=    3,75(футів).

Відповідь: 3,75 футів. 

 

Задача  4 

 Палка  довжиною  0,5  приставлена  до  стіни.  Її  верхній  кінець  на  0,1  зсунули  по  стіні.  На  скільки  відсунувся  від  стіни  нижній  кінець  палки ?

   К                  Розв’язування

  0,1                                                   

  А                    Нехай  СК=АВ = 0,5  -  довжина  палки.                                           Тоді  АК = 0,1;    АС = 0,5 – 0,1 =0,4.  

                           Отже,   ВС² = АВ²  - АС² = 0,5² – 0,4² =                             =  0,25 – 0,16 = 0,09,   ВС =        = 0,3. 

   С                 В

                               Відповідь:  0,3.

 

 

 

 

 

 

 

 

 

                                                 

5.          Важливі  відкриття  Піфагора  та  його  школи

 

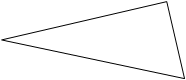
—  Теорема  про  суму  внутрішніх  кутів  трикутника

                                           В

 

            А

                                      С

                                      < A  + <B + <C = 180⁰

—  Несумірність  сторони  квадрата  та  його  діагоналі

    В                    С

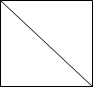
                                                 АВ = 1,    ВD = √2

 

 

   А                 D

—  Метод  доведення  від  супротивного

—  Побудова  середнього  пропорційного  між  двома  відрізками (зокрема, побудова  відрізків  золотої 

пропорції )  

                               С                                      

                            СD  

       

  А             а       D    b      В

 

—  Геометричні  способи  розв'язування  квадратного  рівняння

               ах² + bх + с = 0

—  Побудова  деяких  правильних  многогранників

—  Куля – найдосконаліша  геометрична  фігура. Тому  земля  повинна  мати  форму  кулі

—  Відкриття  досконалих  чисел

Досконалі  числа  -  це  ті  числа,  що  розкладаються  на  суму  своїх  дільників,  крім  самого  себе

  6 = 1+2+3,     28 = 1+2+4+7+14,   

 496= 1+2+4+8+16+31+62+124+248

  6, 28, 496 – досконалі  числа

— Створення   математичної  теорії   музики

Квінта     2:3                             Кварта    3:4

Октава     1:2                            Мала   септима   5:9

Гармонійний   акорд   при  співвідношенні   довжин  струн      3:4:6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6.       Кросворди

 

                                   Кросворд   №1

1.Чотирикутник, у якого дві сторони паралельні, а дві інші – не паралельні. 

2.Найбільша із сторін прямокутного трикутника.

3.Трикутник – це ..., яка складається із трьох точок, що не належать одній прямій, і трьох відрізків, попарно з’єднуючих ці точки.  

4.Одна із сторін трикутника, що утворюють прямий кут.         5.Наука, яка вивчає властивості геометричних фігур. 

         

6.Перпендикуляр, проведений із вершини трикутника на протилежну сторону. 7.Прямокутник, у якого всі сторони рівні.

 

1         6

П

2        4

І

3

Ф

А

5

Г

О

Р

 

     

 

 

 

 

     

 

 

 

 

 

 7

Кросворд   №2

 

1.      Назва прямокутного трикутника зі сторонами 3, 4, 5. 

2.      Учений, ім’ям якого названа теорема про суму квадратів катетів прямокутного трикутника. 

3.      Острів, на якому народився цей математик.

4.      Катет, який не лежить напроти даного кута. 

5.      Там Піфагор пробув 12 років у полоні.

6.      Сторона прямокутного трикутника, яка лежить проти прямого кута. 

7.      Кількість биків, принесена Піфагором у жертву богам після доведення теореми.

 

 

 

Кросворд   №3

 

1.      Назва   прямокутного    трикутника   зі    сторонами пропорційними  числам 3, 4, 5. 

2.      Який  відомий  учений - математик  був  вчителем  Піфагора?

3.      Числа  6, 28,496,…  називаються …………….  

4.      Яка  країна  є  батьківщиною  Піфагора? 

5.      Геометрія  володіє  двома  скарбами:  теоремою  Піфагора  і  ,,золотим ”……………. 

6.      Яке  число  за  теорією  піфагорійців  символізує  розум?

7.      Скільки  років  навчався  Піфагор  у  Єгипті?

 

 

Кросворд   №4 По  горизонталі:

1.  У  якості  символа  піфагорійці  вибрали  …….

3.         Піфагор  -  це  математик  та ………..

4.         У  математиків  арабського  сходу,  ця  теорема  отримала  назву  ,, теореми………”

6.               В  ,,  ……   віршах”  Піфагор  показав  моральні  правила,  суворе  виконання  яких  призводить  до  ідеалу

7.               Учні,  які  називалися  в  школі  Піфагора  називалися…… По  вертикалі:

1.  Іменем  ….   названо  кратер  на  видимій  стороні  Місяця 2.  У   Франції  та  Німеччині   в  епоху  середновіччя   теорему  Піфагора   називали   ,, ослячим   …..”

5.  На  острові  Сицилія  у  Кротоні у  нього  народжується  власна  філософська …….

7.       Поетична  сторінка

 

       У науці, зокрема, в математиці, упродовж віків робилися спроби подачі того чи іншого матеріалу у віршованій формі. Але при цьому, як правило, діяли за принципом, який можна сформулювати так: дощенту зруйнуємо – але заримуємо. Не уникла цієї долі і теорема Піфагора – одна з перлин геометрії. І хоча в більшості її перекладів домінує дидактичний елемент, відсуваючи літературні аспекти на задній план, усе таки трапляються і щасливі випадки, коли поезія гармонійно поєднується з геометрією. До таких винятків, без сумніву, належить сонет відомого німецького поета ХІХ століття Альберта фон Шаміссо.

 

Теорема Піфагора

  Мов світла промінь в темну пору       Приходить істина до нас

Як теорема Піфагора

Вона не схибна  повсякчас.

                За осяйне проміння з неба

                Мудрець на радощах звелів

                Богам віддячити, як треба,-

                Принести в жертву 100 биків.

Відтоді всі бики в тривозі.

І варто істину почуть, Вони утриматись не в змозі, Гуртом розпачливо ревуть.

                Їм мудрі не дають спокою,

                Перлини істини страшать,

                І перед жертвою новою

                Бики примружені тремтять.

Нехай зруйнується століть перепона, Нехай на мить затремтять віки.

Ми знаємо його – Піфагор навколо Він бога творіння, він символ науки.

 

Віват  Піфагору

 

Віват  математиці!

Віват  Піфагору!

Тож  давайте  цій  цариці  заспіваєм  хором:

Найдавніша  ти,  науко В  теоремах,  цифрах  штуках В  логіці  і  силі. Славна  в  кожнім  ділі!

 

Теорему  Піфагора

Знають  всі  народи, Тож  самому  Піфагору Заспіваєм  оду:

Слава,  слава,  руки  вгору, 

Віват,  віват  Піфагору Давньогрецькеє  ім′я Величаєм  ти  і  я.

 

Тож  вивчайте  теорему Мудрості  стихію

Піднімайтесь  на  арену

До  своєї  мрії

І  фортуна  обізветься,

Неодмінно  посміхнеться,

Хай  щастить  Вам,  в  добрий  час, Жде  вас  успіх,  і  Парнас.

 

8.       Цікаво  знати

Чи знаєте Ви, що…

 

…У Франції та Німеччині в епоху середньовіччя теорему Піфагора називали «ослячим мостом»? 

Учнів, що запам’ятовували теорему без розуміння, називали віслюками, оскільки вони не могли перейти через міст – теорему Піфагора.

 

…У математиків арабського Сходу ця теорема отримала назву «теореми нареченої»? 

Справа в тому, що в деяких списках «Начал» Евкліда ця теорема називалась «теоремою німфи» за схожість креслення з бджілкою, метеликом, що грецькою називалося «німфа». Але цим словом греки називали богинь, а також молодих жінок і наречених. Перекладаючи з грецької, арабський перекладач, не звернувши уваги на креслення, переклав слово «німфа» як «наречена», а не «метелик». Так з’явилася лагідна назва відомої теореми – «теорема нареченої».

 

… А  відома    всім  школярам  назва  « Піфагорові  штани  »   виникла  у  Росії? …

  Схожість  креслення  до  Евклідового  доведення  теореми 

Піфагора  зі  штанами  і  дало  назву « Піфагорові  штани  » Відомий  такий  вислів   «Пифагоровы штаны во все стороны равны»

 

 …Довівши свою знамениту теорему, Піфагор віддячив богам, принісши їм у жертву 100 биків? 

 

Це оповідання, найшвидше, вигадка, бо відомо, що Піфагор був вегетаріанцем і непримиренним противником забою та пролиття крові тварин. 

 

…Піфагор був переможцем на 58-х Олімпійських іграх, які проходили в 548 році до нашої ери, а потім перемагав ще на декількох Олімпіадах?

 

Відомо, що Піфагор був міцним юнаком з товстою шиєю та коротким носом, малим на зріст, тому судді однієї   з перших олімпіад     його  спочатку  не  хотіли  допускати  до  змагань,  казали,  що  в  нього  немає,, ні  зросту,  ні  сили,  ні  зовнішності”.  ,, Так,  сказав  Піфагор, -  але  я  буду  наносити  удари  з  математичною  точністю!” 

 Якби це трапилося якихось 2540 років  вперед, газети всього світу вийшли б з аншлагом:   «Нікому не відомий Піфагор завоював золоту медаль у кулачному бою». Ось чому серед  знаменитих  олімпійських  чемпіонів він  довго  залишиться найвідомішим.   Ось чому люди пам’ятають його більше, як дві з половиною тисячі років.   Піфагору  випало щастя перемогти не тільки супротивників, а й перемогти час.

 

… Іменем Піфагора названо кратер на видимій стороні Місяця.

 

 

 

                                      

 

 

 

 

 

 

 

 

 

       

9.  Використана література:

 

1.    Апостолова Г.  Геометрія. – Київ,     ,, Генеза“, 2008. –270с.

2.    Кованцов  М. Учням  про  видатних  математиків. – Львів,  ,,Поліграфкнига”,  1976. – 158с 

3.    Морачова  В.,  Соколовська  І.  Позакласні  заходи  з  математики.  –   Київ,  ,,Редакція  загальнопедагогічних  газет”,  2004. – 128с

5.  Сенчишин  О.  Крокуючи  за  Піфагором.  –  газета  ,, Математика”, №2, 2006. – 24с.