Чотирикутники навколо нас

Тема уроку: Чотирикутники навколо нас. ( Узагальнення теми)

Мета:  систематизувати та узагальнити знання про чотирикутники, їх властивості; формувати здатність самостійно  аналізувати ситуацію, уміння застосовувати набуті знання; сприяти розумінню учнями важливості геометрії в щоденному житті; виховувати мовну культуру та формувати в учнів різні групи компетенцій:

1.     Уміння вчитися- індивідуальний досвід участі в роботі на уроці, бажання організовувати свою працю  для досягнення успішного результату, творчий підхід до розв’язання  проблеми;
2.     загальнокультурні (комунікативні) – опанувати засоби культурного спілкування  в ході обговорення питань уроку, розвивати вміння вести групову бесіду;
3.     соціально- трудові – усвідомлення власного внеску в спільну роботу, готовність робити вибір, уміння відстоювати власну точку зору, прояву ініціативи;
4.     інформаційні – уміння використовувати різноманітну інформацію, аналізувати, систематизувати та узагальнювати її, розширення кругозору.

Тип уроку: узагальнення та систематизація знань, умінь і навичок.

Обладнання: таблиця «Чотирикутники», картки із завданнями, креслярські інструменти, набори геометричних фігур, репродукція картин, вишиті рушники і писанка, кольорова крейда.

Девіз уроку: « Ти можеш, він може, я можу!»

 

ХІД УРОКУ

І.ОРГАНІЗАЦІЙНО – ПСИХОЛОГІЧНА ЧАСТИНА

Учитель. Сьогодні ми працюватимемо разом. Кожному з вас хочу побажати, щоб на уроці вибули:

«У»- усміхненими,

«С»- спокійними,

«П»- прогресивними,

«І»- ініціативними,

«Х»- хоробрими.

Генрі Форд  говорив:

«Збиратися разом- це початок,

Триматися разом – це процес,

Працювати разом- це успіх».

Іншими словами, я бажаю вам УСПІХУ!

ІІ. ПІДГОТОВКА ДО ВСІДОМОЇ НАВЧАЛЬНОЇ ДІЯЛЬНОСТІ: ПОВІДОМЛЕННЯ ТЕМИ УРОКУ, ВИЗНАЧЕННЯ МЕТИ ТА МОТИВАЦІЇ НАВЧАННЯ

Учитель. Досягнути успіху можна тільки тоді, коли є певна мета. Тому ознайомимося з темою уроку та сформулюємо нашу мету.( Діти висловлюють свої думки).

-         Ми завершили вивчення теми» «Чотирикутники». Сьогодні маємо  узагальнити, систематизувати вивчене, вчитися використовувати набуті знання та вміння в незвичайних  і несподіваних ситуаціях, перевіряти теоретичний матеріал і застосовувати його до практичних вправ.

Різні  властивості чотирикутників досліджували не тільки шанувальника геометрії, а найвідоміші вчені епох: Евклід, Ньютон, Ейлер, Гаусс, Лагранж та інші. Виявлені та досліджені ними властивості чотирикутників – справжні перлини людського мислення. Багато з них доступні для розуміння вам, і ми їх вивчили. Геометрія чотирикутника дає чудовий матеріал для досліджень, у них можна знайти цікаві  й доступні теми для самостійних пошуків.

 На уроці присутні експерти: дизайнер,  художник, біолог, мистецтвознавець, етнограф, конструктор, архітектор. Члени групи більш досконало вивчали чотирикутники, встановили нові факти, написали звіт про своє дослідження і сьогодні повідомлять   їх нам.

-         А зараз відкривайте зошити, записуємо дату та тему уроку.

 

ІІІ. ВІДТВОРЕННЯ ТА КОРЕКЦІЯ ОПОРНИХ ЗНАНЬ

Повторимо теоретичні відомості, що знадобляться протягом уроку для виконання завдань.

1. Колективна пошукова робота

Розглянемо таблицю і виконаємо завдання ( рис1.)

Назвіть зображені фігури.

1. Запишіть умови, які використовуються для означення зображених чотирикутників.  Відповідь: АВ | | CD   BC| |AD.
2. АВ | | CD   , BC| |AD, <А=<В=90°.
3. АВ | | CD ,    BC| |AD., <А=<В=90°, АВ=ВС= CD=АD.
4. АВ | | CD  , AD| |,    BC, АВ=ВС= CD=АD.

 

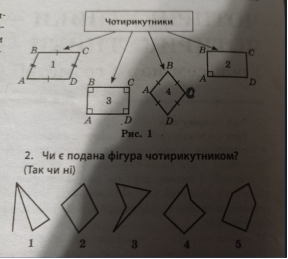
2. Чи є подана фігура  чотирикутником? (Так чи ні)
3.  Гра «Художник – геометр»

Колективна робота.

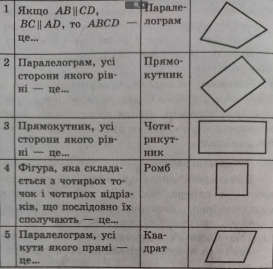
Усі ви, відвідували уроки образотворчого мистецтва. А зараз ви побуваєте в ролі художників- геометрів. На дошці зображена таблиця, яка потребує ваших знань геометрії і творчих здібностей. Треба визначити ,  про яку геометричну фігуру йдеться, сполучити стрілками вислови із назвою фігури та її зображення. Кожен учень рисує одну стрілку.

 

4. Усе, що знаю про неї скажу

Інтерактивна вправа «Мікрофон»

   Розкажіть  усе , що знаєте про геометричні фігури – трапецію, паралелограм, ромб, квадрат, прямокутник: зображення, означення, властивості , цікаві факти.

(Розповіді учнів про геометричні фігури заздалегідь підготовлені).

 

5. Індивідуальна перевірка знань.

Учні заповнюють узагальнюючу таблицю  з теми чотирикутники. Позначити знаком «+» властивості, характерні для поданих фігур.

 Таблиця     

 

Властивості	Види фігур
	Паралелограм	Прямокутник	Ромб	Квадрат
Чотирикутник
Протилежні сторони попарно паралельні
Усі кути прямі
Усі сторони рівні
Діагональ ділить на два рівних трикутники
Протилежні сторони і кути рівні
Діагоналі точкою перетину діляться навпіл
Сума кутів, прилеглих до однієї сторони, дорівнює 180°
Діагоналі рівні
Діагоналі взаємно перпендикулярні
Діагоналі є бісектрисами кутів

 

6. Логічна гра «Чотирикутник»

 У завданні сформулюйте відповідні пари з виразів лівого і правого стовпців так, щоб утворилися правилі твердження.

А)У чотирикутнику протилежні сторони рівні	1) Тоді в нього можна вписати коло
Б) У чотирикутнику всі сторони рівні	2)Тоді він є квадратом
В) У паралелограма діагоналі рівні і є бісектрисами його кутів	3)Тоді він є паралелограмом
Г) Суми протилежних сторін чотирикутника рівні	4)Тоді навколо нього можна описати коло
Д) Сума протилежних кутів чотирикутника дорівнює 180°	5)Тоді він є ромбом

 

7. Виключте зайве слово

1.     У ромба, квадрата, прямокутника, рівнобічної трапеції діагоналі рівні.
2.     У ромба, прямокутника, квадрата сторони рівні.
3.     У ромба, паралелограма, квадрата діагоналі перетинаються під прямим кутом.
4.     Які із зображених на рис. 2 чотирикутників є трапеціями? Які з них прямокутні, які рівнобічні?

Прямокутник називають золотим, якщо відношення його сторін а і в дорівнює 1,62, тобто а/в=  корінь квадратний з 5+1поділене на 2=1,62.       Ще стародавні греки вважали, що прямокутники , довжини сторін яких утворюють відношення золотого перерізу , є найприємнішими для ока. Тому такі форми є  найбільш поширеними – від книжкових обкладинок  до письмових столів, від вікон до фасадів будинків, від кредиток до гральних карт тощо.

 Перпендикулярність діагоналей ромба застосовують у чотириланкових шарнірних механізмах для реалізації  прямолінійного поступального руху. Одним з найпоширеніших  прикладів такого застосування є домкрат. , інший приклад- механізм відцентрового регулятора (епоха парових машин, Джеймс Уатт, для регулювання подачі пари  у паровій машині).

 

***Розв’язання усних вправ

1.     Із фанери випиляли квадрат. Як перевірити, що відрізаний чотирикутник є справді квадратом? (Повернути чотирикутник на 90° і встановити в розріз, що утворився у фанері.)
2.     Майстер – паркетник хоче впевнитися в тому, що чотирикутники, які він випиляв, є квадратами. Чи достатньо для цього :

А) рівності чотирьох сторін; ( ні, чотирикутник може бути ромбом).

Б) рівність двох діагоналей; (ні, чотирикутник може бути прямокутником).

В)рівності чотирьох сторін та рівності двох діагоналей? ( так).

**** Розв’язування пошукових задач

 Робота в парах

-         Як із прямокутного куска тканини вирізати квадратну хустинку, користуючись лише ножицями?

IV. ВИКОРИСТАННЯ НАБУТИХ ЗНАНЬ І НАВИЧОК ПІД ЧАС РОЗВ´ЯЗУВАННЯ ЗАДАЧ

 

-         Розв’язування геометричних задач

 

1. Доведіть , що на рисунку зображено паралелограми.

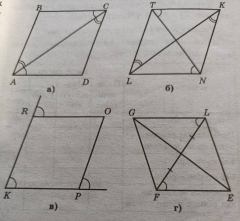
2. Три кути чотирикутника дорівнюють 28°, 62°,70°. Знайдіть четвертий кут. Чи може він бути опуклим?
3. Знайдіть кути трапеції, якщо:

А)один кут дорівнює 100°, а трапеція прямокутна;

Б) один кут трапеції дорівнює 45°, а трапеція рівнобічна.

 

4. У трапеції  основи ВС=15 см; АД=23 см. Знайдіть середню лінію MN.

 

-         Розв’язування практичних задач

Французький математик Рене Декарт(1596-1650) писав: «.. у математичних науках є дуже вдалі винаходи, здатні принести велику користь, задовольняючи любов до знань, полегшуючи всі ремесла і скорочують працю людини».

-         Є предмети і деталі, що містять моделі паралелограмів ( шарнірна модель, дротяна сітка, віконна рама..), трапеції (мостова ферма, пасова передача, кронштейн..).

-         Вивчені властивості на ознаки паралелограма мають численні практичні застосування: у конструкції відкидних драбин, які застосовують у пасажирських залізничних вагонах; у столярній та будівельній справі ( двері, перила на східцях), для креслярських приладів ( креслярські лінійки).

    «Нежорсткість» чотирикутника. Уявіть модель чотирикутника, зроблену із  шарнірно сполучених планок. Ми можемо  змінювати величини кутів чотирикутника, а довжини сторін залишаться без змін. Це свідчить, що існує  безліч таких чотирикутників із заданими довжинами сторін. На відміну від чотирикутника, трикутник є жорсткою фігурою.

-         Найпоширенішим видом  чотирикутників є прямокутник. Ще давні  єгиптяни надавали своїм земельним ділянкам  прямокутної форми. Прямокутну форму мають  плани і більшість складових  архітектурних споруд як давнини,  так і сучасності, зокрема школа. Прямокутник є визначальним  структурним елементом прямокутного паралелепіпеда.

Ділова гра »Настилання паркетної підлоги»

Завдання. Виконати настилання паркетної підлоги в залі, який має форму прямокутника. Паркетні плитки мають форму прямокутних трапецій, паралелограмів, рівнобедрених трапецій. Після настилання підлоги не повинно лишитися зайвих плиток і проміжків  між ними.

 

 

 

 

  Геометричний тренінг

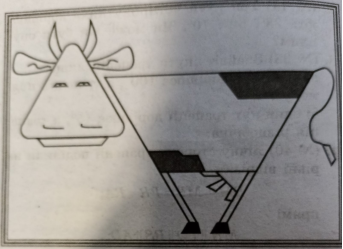
Трапеція – священна фігура піфагорійців. У кожній оселі оселі обов’язково було що – небудь « трапецієподібне», що захищало членів родин  від усіх бід і негаразд. У нас є «священна « картина тих часів. Покажіть , де на ній зображено трапеції.( 12 трапецій).

 

 

 

V. Чотирикутники навколо нас.

Біолог. Невідомий досі вид дерев зі стовбурами, що мають не круглий, а квадратний переріз, доглядають ботаніки в провінції Чжецзян к Китаї. Тут, на площі близько 50 квадратних метрів, росте 120 таких дерев заввишки 3-5 метрів. Дерево з чотиригранними стовбуром- це ж готова шпала, що не потребує обробки!

      У  Японії «квадратні кавуни» вивів селекціонер Томоюкі Оно, не використовуючи при цьому жодних хімікатів. Такого результату він досяг, вирощуючи кавуни у спеціальнихквадратних скляних горщиках. Вони зберегли смак, але набули нових переваг: зручно ділити на часточки, легко відділяти шкірку, викладати для транспортування. В Ізраїлі вирощують «квадратні «помідори. На замовлення авіакомпанії генетики у США вивели сорт кукурудзи з «квадратними «зернами. 

     У  живопису велику роль відіграє формат картини, і вибирають його художники дуже ретельно.  Найчастіше вони надають  перевагу прямокутному( вертикальному, горизонтальному) формату, колу(тондо). У прямокутниках компонують зображення в тій чи іншій геометричній формі, іноді розгортають дію по діагоналі. Формат картини пов'язаний зі стилем епохи, з особливостями техніки живопису, композиції, інтер´єру для якого призначена картина.

      А зараз ми відвідаємо музей однієї картини-  всесвітньо  відомої , майже легендарної… Це картина «Чорний квадрат», Малевича. Придивіться . Комусь квадратбачиться страшною дірою, а комусь бездонною криницею, в яку хочеться впасти – так вона тремтить і вабить.  Квадрат має всі ознаки образу – як квітка чи акорд. Це початок  напямку супрематизму-  вид абстрактного мистецтва 20 століття: комбінування зафарбованих найпростіших геометричних фігур( квадрата, смуг, трикутника тощо.). Цей стильвплинув на розвиток декоративно – оздоблювальног мистецтва на стиль меблів, посуду, одягу, зачісок і навіть на оформлення друкованих видань різнокольорової тари, що має чотирикутні форми. Таких квадратів офіційно відомо щонайменше п´ять.

 

 

 

Дизайнер. Вишивка – оди з давніх і найбільш розповсюджених видів мистецтва. Вона виникла давно і передавалася від покоління до покоління. Ще в глибоку давнину люди навчилися створювати нескладні малюнки з умовних знаків- символів, де  кожна лінія чи фігура мала лише певне значення. Так, сонце зображували у вигляді ромба або квадрату. Ромб з подовженими сторонами  означає будівлю, а квадрат, розділений на чотири частини з крапкамив кожній , символізував засіяне поле чи садибу.

     У нашому класі представлені рушники, що збереглися в родині. У вишивці майстрині відтврили свої заповітні мрії про майбутнє. Розгляньте на рушнику геометричні узори , поясніть їх значення.

   Етнограф. Писанка- мистецьки розписані великодні яйця. Гляньте, які писанки різні за орнаментом. Ці орнаменти – не просто малюнки, а таємничі знаки.

           Знаки долю прихиляють,

          Лихо відвертають.

     Досить популярними є геометричні символи: яйце ділиться простими лініями на трикутники, квадрати , ромби , пояски.» Ромб» є символом родючості.  «Квадрат», поділений на частини з крапками, був символом засіяного лану( малюнок).

  VІ. ПІДБИТТЯ ПІДСУМКІВ УРОКУ

1. ПОЯСНІТЬ ДІАГРАМУ

 

 

 

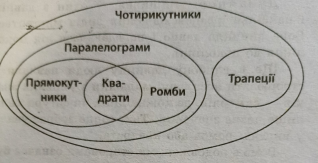
2. Інтерактивна вправа «Мікрофон»

  Запитання

1.     Чи потрібно вивчати властивості чотирикутників?
2.     Чи потрібно цю тему включти до шкільної програми?

 

3. Усвідомлення результатів уроку( релаксація)

-         Що ми робили на уроці?

-         Чому ми цим займалися?

-         Що споюобалося і що не сподобалося на уроці?

-         З ким приємно було працювати?

-         Які ваші пропозиції?

4. Виставлення оцінок роботи учнів.

Учитель оцінює роботу учнів.

   На високому рівні виявили свої творчі здібності, уміння розв´язувати задачі такі учні….

На достатньому рівні вміють узагальнювати і систематизувати  навчальну інформацію , формулювати і застосовувати основні властивості чотирикутників….

  VІІ. ДОМАШНЕ ЗАВДАННЯ

1. Повторити ГОЛОВНЕ В ПАРАГРАФІ 1, с. 71-74.
2. Пошукове завдання. Знайти відношення сторін предметів прямокутної форми та порівняти з числом 1,62. Зробити висновок.

Учитель. Мудрець сказав: « Дві людини, які обмінялись золотими монетами, не стали багатшими. Але якщо вони обмінялись  думками, то кожен з них став вдвоє багатшими. Адже обидва стали тепер розумнішими».

-         Ця притча проста, але зміст її глибокий . Обмінюючись думками, ідеями, досвідом, знаннями, люди нічого не втрачають, а багато чого набувають – нових знань.

    Ось і ви сьогодні дізналися багато нового про чотирикутники. Сподіваюсь, що кожен з вас щоденно наполегливо підніматиметься по крутих схилах науки геометрії, впевнено крокуючи до нових знань.

Бажаю вам успіхів освоєнні «геометричного океану знань». Урок закінчено, до зустрічі на наступному уроці!