Презентація до уроку геометрії 10 класу «Кут між площинами».
Про матеріал
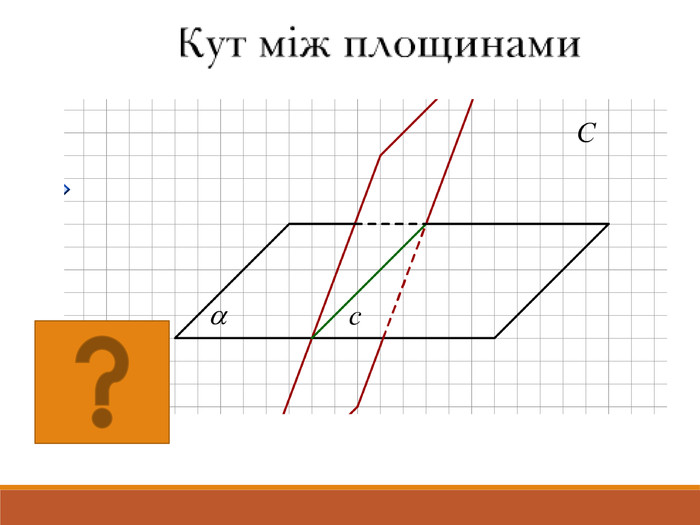
Презентація до уроку геометрії 10 класу «Кут між площинами».
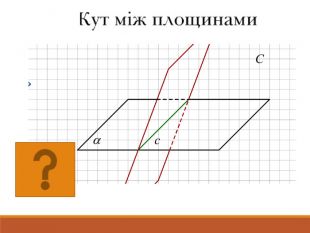
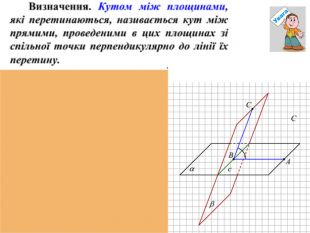
Мета уроку: -формування поняття кута між площинами та вмінь учнів знаходити кути між площинами;
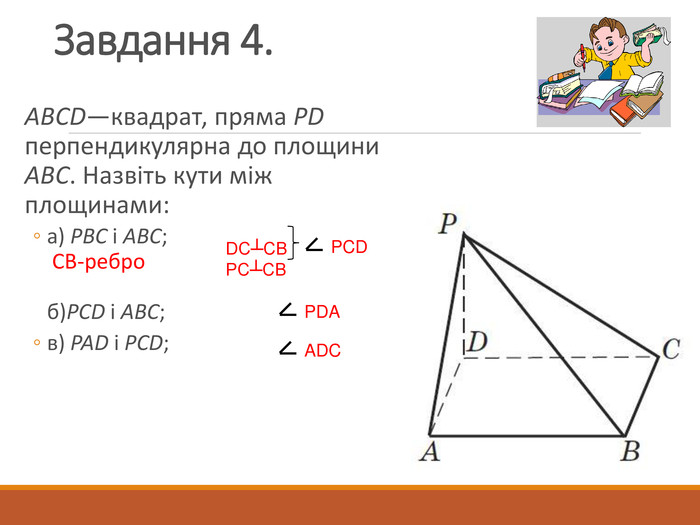
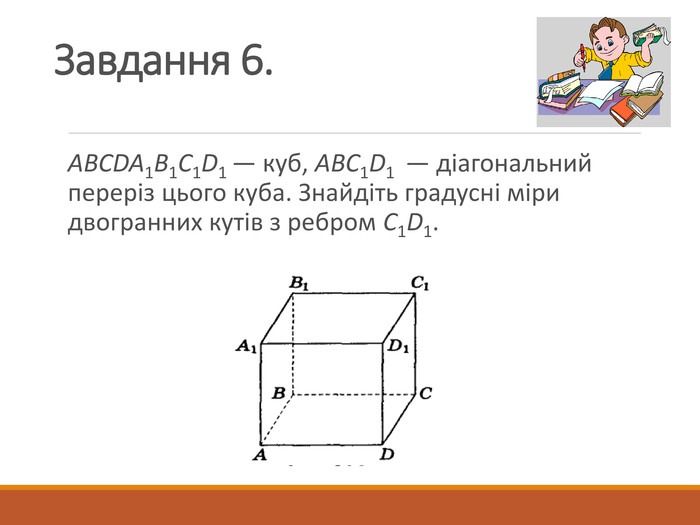
-сприяти розвитку в учнів просторової уяви, вміння знаходити даний кут на зображенні, на моделі;
-сприяти вихованню графічної культури учнів, домогтися чіткості формулювань введених означень.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
До підручника
Геометрія (профільний рівень) 10 клас (Бевз В.Г., Бевз Г.П., Владімірова Н.Г., Владіміров В.М.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку






























-

Вашека Антоніна
03.12.2024 в 13:08
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Вашека Антоніна
03.12.2024 в 13:08
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Вашека Антоніна
03.12.2024 в 13:08
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Вашека Антоніна
03.12.2024 в 13:08
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Вашека Антоніна
03.12.2024 в 13:08
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Вашека Антоніна
03.12.2024 в 13:08
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Андрейченко Тетяна Олексіївна
05.12.2022 в 12:47
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Лебедева Юля
07.11.2022 в 09:19
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Shaga Tanya
08.02.2022 в 09:30
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Давиденко Олександр Анатолійович
12.01.2021 в 08:50
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сібєнкова Любов Сергіївна
06.04.2020 в 21:18
Загальна:
4.0
Структурованість
4.0
Оригінальність викладу
4.0
Відповідність темі
4.0
Показати ще 8 відгуків