ПЛАН УРОКУ

 

Дата «____»_________________ 20__ р.

Предмет:   Геометрія

Тема: Паралельність прямих і площин у просторі

Тема уроку:  Паралельне проектування та його властивості Мета уроку:

-                      ознайомити учнів із поняттям паралельного проектування та його властивостями, навчити учнів застосовувати знання з теми для розв’язування задач; показати широке коло застосування властивостей паралельного проектування у навколишньому світі.  

-                      Розвивати індивідуальні здібності та пізнавальну активність учнів, просторову уяву, вміння висловлювати свою думку, логічне мислення, вміння використовувати свої знання з геометрії при вирішенні прикладних завдань в різних сферах діяльності.

-                      Виховувати творчу, працелюбну особистість шляхом навчання за допомогою швидкозмінних форм подачі інформації.

Тип уроку: урок вивчення нового матеріалу

Вид уроку: лекція  з елементами проблемних питань та пошукового практикуму.

Методи: словесні (діалог, монолог), наочні, частково пошукові, евристичні, практичні

Дидактичне        забезпечення:     робочий      зошит         з        теми «Паралельне проектування», презентація викладача

Обладнання:ноутбук, проектор, екран

      

                                                                    «Не досить оволодіти премудрістю,

потрібно також вміти користуватись нею…»

                                                                                                          Рене Декарт                                                                    (французький філософ, математик,

фізіолог, фізик) 

Хід уроку

I. Організаційний момент.

Повідомлення теми і мети уроку.  

ІІ. Актуалізація  знань. 

Виконайте вправу на відповідність: «Закінчіть речення…»

ЗГАДАЙТЕ, ЗНАДОБИТЬСЯ!

ЗАКІНЧІТЬ РЕЧЕННЯ…	ВІДПОВІДЬ
1. Стереометрія – це розділ геометрії, в якому вивчаються…	А) точка, пряма, площина
2. Пряма і площина називаються паралельними, якщо вони…	Б) добуток середніх членів дорівнює добутку крайніх
3. Основні фігури стереометрії…	В) не перетинаються і не лежать   в одній площині
4. Основна властивість пропорції…	Г) рівносторонній
5. Прямі паралельні, якщо вони…	Д)  прямий
6. Вписаний кут, що опирається на діаметр…	Е) не перетинаються
7. Прямі мимобіжні, якщо вони…	Є) не перетинаються і лежать в одній площині
8. Правильний трикутник - це…	Ж) властивості фігур у просторі

 

III. Мотивація навчальної діяльності.

Ми неодноразово зустрічаємося з паралельним проектуванням у житті. Наприклад, наша тінь у сонячний день на рівному асфальті є нашою паралельною проекцією, оскільки  сонячні промені наближено можна вважати паралельними зважаючи на велику віддаленість Сонця від Землі.  У дитинстві ми всі любили грати з тінями, показуючи за допомогою рук кілька класичних фігур - собачку, зайчика, пташку. Людські руки здатні створити на освітленій стіні дивовижний світ, причому неймовірно реальний. Театри тіней створюють дивовижні силуетні образи за допомогою власного тіла. (Демонстрація відеоролика: «Я - українець»  фрагменту вистави

Київського театру тіней)

  Зобразити тривимірний об’єкт на плоскому кресленні з абсолютною точністю неможливо. Однак за допомогою плоского рисунка можна одержати досить чітке уявлення про окремі властивості плоских фігур. Щоб плоскі рисунки давали якомога чіткіше уявлення про властивості тієї чи іншої просторової фігури, необхідно знати правила зображення просторових фігур на площині.  Ними користуються художники, що малюють тінню… Вони порушують  усі можливі закони мистецтва. Адже «пишуть» двовимірні картини за допомогою тривимірних скульптур, і їх улюблений «матеріал» - це тінь ... Колекції створені за допомогою ламп та розкладеного непотрібу.

 Їхні роботи - спроба створити досконалу красу з відвертого сміття.

(Вернісаж робіт голандця Дієт Вігмана, азербайджанця  Рашада Алакбарова,  грецького художника Теодосія Ауреа (Teodosio Sectio Aurea))      IV. Сприйняття й усвідомлення нового матеріалу.

Допоміжним засобом є презентація викладача, створена у програмі Power Point (ілюстративний матеріал до уроку, перевірка виконаних завдань). 

Учні працюють в робочих зошитах. 

Пояснення і осмислення навчального матеріалу відбувається за допомогою інтерактивних методів: виконується вправа на відповідність,  проводяться пошуковий практикум і графічний диктант, знаходяться відповіді на проблемні питання, розв’язуються задачі-тести.  Лекція викладача з елементами бесіди та тестових питань.

 Теоретичні відомості 

Ми вивчаємо стереометрію – геометрію у просторі. Як завжди нам необхідно вміти зображувати геометричні фігури, причому всі креслення ми і досі  виконуємо на площині (на сторінці зошита, на дошці тощо). Яким чином  просторову фігуру (наприклад , куб) можна «вкласти» до площини? Для розв'язання цієї задачі приймається метод паралельного проектування. Паралельне проектування — це зображення довільної геометричної фігури на площині, при якому всі точки фігури переносяться на площину за прямими, паралельними заданій, яку називають напрямом проектування.

Пряма a задає напрям проектування, α — площина проекції. 

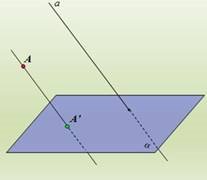З'ясуємо  суть метода паралельного проектування  на прикладі найпростішої  геометричної фігури – точки. Оберемо у просторі довільну площину (її ми будемо називати площиною проекцій) та довільну  пряму a∩

 (вона задає напрямок паралельного

проектування).  Проведемо через точку А пряму, паралельну до прямої а.

Точка А′ перетину цієї прямої з площиною  є проекція точки А на площину . Точку А ще називають прообразом, а точку А′ – образом. Якщо А, то А′

співпадає з А. 

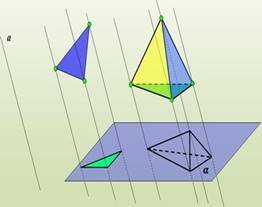Якщо розглянемо будь-яку геометричну фігуру як множину точок, то можна побудувати в заданій площині проекцію даної фігури. Таким чином можна отримати зображення (або «проекцію») будь-якої площини або просторової фігури на площині.

Зауваження 1. При паралельному проектуванні не обирають напрямок  паралельного проектування паралельно до площини проекції (самостійно поясніть чому).

Зауваження 2.При паралельному проектуванні плоских фігур не обирають напрямок паралельного проектування паралельно до площини, в якій лежить ця плоска фігура, оскільки проекція, яка при цьому отримується, не відображає властивості даної плоскої фігури. Таку проекцію називають виродженою.

Зауваження 3.Якщо напрямок паралельного проектування

перпендикулярний до площини проекцій, то таке паралельне проектування називаєтся ортогональним(прямокутним) проектуванням.

Зауваження 4.Якщо площина проекцій та площина, в якій лежить дана фігура, паралельні ( ||(АВС)), то зображення, яке при цьому отримаємо, дорівнює прообразу.

Властивості паралельного проектування:

1)відрізки зображаються відрізками;

2)                паралельні відрізки – паралельними відрізками або відрізками  однієї прямої;

3)                відношення довжин відрізків, які лежать на паралельних або на одній прямій, зберігається;

4)                Лінійні розміри плоских фігур (довжини відрізків, величини кутів) НЕ  зберігаються (виключення: якщо площина проекцій та площина, в якій лежить дана фігура паралельні).

 

 

V. Осмислення нового матеріалу.

1.Тест (колективна робота) 1) В якому випадку паралельною проекцією прямої буде точка?

А) Якщо пряма паралельна напрямку проектування

Б) Якщо пряма паралельна проектуючій площині 

В) Якщо пряма перетинає площину проекцій

Г)  Якщо пряма перетинає пряму, що задає напрямок паралельного проектування

2)  Скільки точок можна отримати при паралельному проектуванні трьох різних точок простору?

А) Три

Б) Одну

В) Три, або дві, або одну

Г) Дві

3)  Які фігури можуть бути паралельними проекціями прямих, що перетинаються?

А) дві прямі, що перетинаються

Б) одна пряма

В) дві паралельні прямі

Г) дві прямі, що перетинаються, або одна пряма

4) 

Яка фігура не може бути паралельною проекцією трапеції? (В)

                 А)                   Б)                    В)                           Г)                                        

5)  Яка фігура не може бути паралельною проекцією правильного трикутника, у якого проведена одна  висота?  (Б)

А)                            Б)                          В)                           Г)                                         7) Зображенням якого трикутника є ∆АВС, якщо точка В лежить на еліпсі, а АС – діаметр цього еліпса

А) ∆АВС – зображення гострокутного ∆, вписаного в коло

Б) ∆АВС – зображення тупокутного ∆, вписаний в коло

В) ∆АВС – зображення прямокутного ∆, вписаного в коло

Г) ∆АВС – зображення гострокутного ∆, описаного навколо кола

 

2. Проблемне питання (додатково)

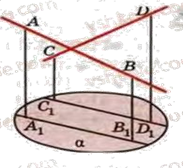Чи перетинаються прямі АВ і СD, зображені на малюнку, якщо А₁ B₁ і C₁ D₁ – їхні проекції на площину ? 

Розв’язання:  

Припустимо, що прямі АВ і СD перетинаються. Тоді проекція точки їх перетину повинна лежати на проекціях прямих .

А оскільки проекції А₁ B₁ і C₁ D₁  паралельні (не мають спільних точок), то прямі АВ і СD не перетинаються.

Отже, прямі АВ і СD – мимобіжні, і їх паралельною проекцією є паралельні прямі.

Які ще фігури можуть бути паралельними проекціями мимобіжних прямих? 

Відповідь: прямі, що перетинаються; пряма і точка

Як повинні розташовуватись мимобіжні прямі, щоб їх проекцією на площину були пряма і точка? 

Відповідь: Одна з них повинна бути паралельною напрямку проектування

 

3. Пошуковий практикум (додатково )

Паралельною проекцією точок А, В і С (точка С лежить між А і В) на

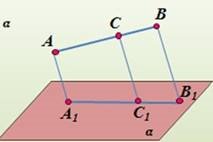площину    є точки А₁, B₁ і C₁ . Знайдіть А₁B₁ і

А₁C₁, якщо АВ = 20 см,  ВС = 8 см, а B₁C₁ = 2 см) Розв’язання: 

За 3-тьою властивістю паралельного проектування (про пропорційні відрізки)

 АВВС= АВ1𝟏ВС1𝟏 . Тобто , А  = 5

(см)  

    

Тоді А C = А B - B C = 5 – 2 = 3 (см)     Відповідь: 5 см; 3 см

                 1    1           1    1         1    1

   Графічний диктант  «Вірю – не вірю»  ( за кожну вірну відповідь – 1 бал)

1)  При паралельному проектуванні зберігаються   величини кутів (ні)

2)  При паралельному проектуванні зберігаються довжини відрізків (ні)

3)  Паралельна проекція кута може бути більше (менше) самого кута (так)

4)  Паралельна проекція відрізка може бути більше (менше) самого відрізка (так)

5)  При паралельному проектуванні відрізків можна отримати точки (так) 6) Паралельна проекція квадрата може бути трапецією (так)

7)                Паралельною проекцією двох паралельних прямих можуть бути  прямі, що перетинаються (ні)

8)                Паралельною проекцією трапеції з основами  4 см і 8 см може бути трапеція з основами 2 см і 6 см (ні)

9)                Паралельною проекцією правильного трикутника  з Р =12 см може бути тупокутний трикутник з Р = 21 см (так)

10)            Якщо точка С належить відрізку АВ, С′ - проекція точки С, А′ - проекція точки  А, В′ - проекція точки В, то точка С′ належить відрізку А′В′ (так)

 

Перевірка у парах

 

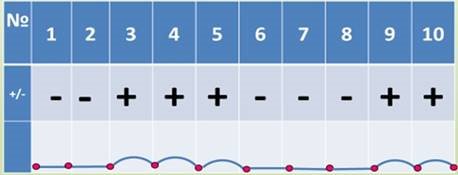
VII. Підбиття підсумків  уроку - Роз’яснення незрозумілих питань.

-         Самооцінювання робіт учнями.    

-         Оголошення оцінок за урок.

Твій настрій:  

                                     

                       САМООЦІНКА:                ОЦІНКА ВИКЛАДАЧА:

VIII. Домашнє завдання.

1.            Підручник під редакцією Г. П. Бевза «Математика 10 кл.»,  задача №851, 854

2.            Творче завдання:  

Зобразіть паралельну проекцію друкованої літери, з якої починається ваше прізвище 

 

                                 Укладач: викладач математики                      С.І. Гадалін