Урок "Перетворення графіків функцій"

 

 

 

 

 

 

 

 

ПЕРЕТВОРЕННЯ

ГРАФІКІВ ФУНКЦІЙ

 

 

                                                                                               

                                                                      

 

                                                                        Урок алгебри у 9 класі

                                                                        Вчитель математики

                                                                                Коваленко

                                                                        Анастасія Григорівна

 

 

 

 

 

                

 

          Мета уроку:

• повторити  та систематизувати знання та вміння учнів з вивченої теми, вдосконалити навички розв’язування вправ, що передбачають: побудову графіка функції;   дослідження функції,  перетворення графіків функцій;
• розвивати  мислення, пам'ять, кмітливість, увагу, ініціативність, самостійність, вміння об’єктивно проводити самоконтроль власної діяльності;
• виховувати наполегливість, зосередженість, дисциплінованість, культуру мовлення,  навички колективної роботи та співпраці, формувати пізнавальний інтерес.

 

Тип уроку: урок-практикум

 

Наочність та обладнання:  мультимедійний проектор, комп’ютерна презентація, роздатковий матеріал,  картки, ескізи графіка функції у=.

 

Епіграф:  Мало знати, потрібно й використовувати.

                   Мало бажати, потрібно й робити.

                                                                  Й.Гете.

Хід уроку

 

1. Організаційний етап.

Організація уваги учнів. Перевірка готовності класу до уроку.

Учитель. Доброго дня! Сьогодні в нас урок незвичний, до кожного етапу я дібрала вислів відомої людини. Отже, починаємо ми з вислову Давньокитайського філософа Конфуція: «Від того настрою, із яким ви вступаєте в день, або в якусь справу, залежать ваші успіхи, а можливо, і невдачі». Я бажаю вам розпочати урок із хорошим настроєм і отримати міцні знання і гарні результати.

 Доторкніться долонями до сусіда. Так ми віддамо частинку свого тепла один одному, одержимо позитивну енергію на цілий урок та побажаємо кожному успіхів на уроці.

 

2. Оголошення теми і мети уроку. Мотивація навчальної діяльності.

            Алгебра , як і інші науки, дає нам нові знання, нові вміння та відкриває нові можливості їхнього застосування на інших уроках, у практичному житті. Щоб знання можна ефективно застосовувати, їх потрібно добре засвоїти. Конфуцій сказав: «Я чую-і я забуваю, я бачу- і я запам’ятовую, я роблю- і я розумію», щоб наш урок був плідним, скористаємося цим мудрим висловлюванням і працюватимемо за принципом: я слухаю – я бачу – я роблю – я розумію.

На попередніх уроках ми розглянули найпростіші перетворення графіків функцій. Сьогодні наше завдання закріпити та вдосконалити наші знання та вміння.

Для того, щоб ви добре повторили й закріпили вивчений матеріал,  я вам хочу побажати впевненості і творчої роботи на уроці. А також бути компетентними, тобто готовими застосувати набуті знання, вміння та навички для виконання теоретичних і практичних завдань. Я буду вашим помічником .  Коли починаєш справу, спитай себе: «Що я маю зробити?», після закінчення: «Що я зробив?» Піфагор.(давньогрецький математик)

• Які завдання, на вашу думку, вам треба поставити перед собою?

Очікуванні відповіді

• Я хочу навчитися будувати графіки функцій.
• Я хочу навчитися досліджувати функції.
• Будувати ланцюг перетворень
• Розпізнавати на малюнках графіки функцій.
• Навчитися будувати графіки деяких функцій швидко.
• Читати графіки функцій…

Працюючи на уроці не забувайте в оцінний аркуш для самоконтролю записувати кількість балів на кожному етапі уроку .

 

 Актуалізація опорних знань.

Відомий  фізіолог ІванПетрович Павлов писав: «Ніколи не беріться за подальше вивчення, не засвоївши попереднього». Отже перевіримо, наскільки ви компетентні в тому матеріалі,що вивчили з теми.

1.Вправа «Разом веселіше»

              Тест 1 «Пригадай назву» (пригадати функції і назви видів ліній, які є графіками цих функцій )

 

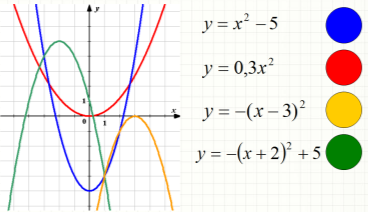
Тест 2 «Встановити відповідність»

(поставити у відповідність до кожного графіка аналітичний запис відповідної функції )

                                    

                                          1.Е  2.А  3.Б  4.Ж  5.Д   6.Є  7.В  8.Г

 

                А тепер  зробимо «математичну зарядку», щоб повторити опорні знання теоретичного матеріалу, які нам необхідні на уроці.

 Вправа «Так, ні» графічний диктант

Хоч слова «так» і «ні» короткі, усе ж вони вимагають серйозних роздумів.

          Запитання                                                                     Піфагор

1. Область визначення функції у= 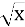є множина всіх дійсних чисел(-)
2. Область значень функції у= 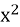є множина всіх дійсних чисел(+)

     3.Значення аргумента при якому значення функції дорівнює нулю наз. нулями функції.(+)

    4.Проміжок на якому функція зберігає знак, наз. проміжком знакосталості функції(+)

    5.Функцію наз. зростаючою на деякому проміжку, якщо  на цьому проміжку більшому значенню аргумента відповідає менше значення функції.(-)

    6. Для побудови графіка функції у=f(х)+n, де n >0, достатньо графік функції у= f(х) перенести вздовж осі у на п одиниць вгору(+)

    7.Для побудови графіка функції у=f(х+m), де m<0, достатньо  графік фунуції у= f(х) перенести вздовж осі  х на  m одиниць вліво.(-)

   8.Графіки функцій у= f(х) і у=-f(х) симетричні відносно осі у (-)

   9.Щоб побудувати графік функції  у= ‌‌‌f(х)І достатньо побудувати графік функції у= f(х) і ту його частину, яка лежить нижче осі х, симетрично відобразити відносно цієї осі.(+)

 

 

Тест 4

Бернанд Больцано – чеський математик. На жаль, за  своє життя він надрукував тільки 5 невеликих математичних творів. Велика математична праця «Вчення про функції», яка була написана 1830 році, побачила світ тільки через 100 років. Саме Б. Больцано належить фраза «Формула іноді здається більш мудрою, ніж людина, яка її придумала»

 

Добре. Ми повторили найнеобхідніше. Не забудьте оцінити свої теоретичні знання.

 

3. Застосування знань,закріплення вмінь та навичок.
4. Видатний математик Олексій Миколайович Крилов сказав: «Для теорії необхідні знання,для практики, крім цього, ще й уміння». Його педагогічне кредо – «навчити вчитися»

В сучасній математиці вивченню функцій приділяється особлива увага, адже за їх допомогою можна змоделювати явища, які відбуваються в природі, на виробництві та в суспільстві. Побудова графіків значно полегшує процес вивчення функцій. Спробуємо навчитись будувати графіки деяких функцій швидко і легко.

 «Побудова та дослідження»

1. Скласти ланцюжок перетворення для функції

у= +2                 у=           у=+6               у=+5

ֹ 2.Побудувати графік функції:

у= -(х-3)²+4.

Користуючись графіком, знайдіть:

а) Область визначення функції;

б) Область значень функції;

       в) усі значення х, при яких функція набуває від’ємних та додатних значень;

г) проміжки, на яких функція спадає та зростає

д)найменше, найбільше значення

3. Побудувати графік функції у=I+8х+15I

                Колективна робота «Розв’язування задач практичного змісту». Розглянемо зображення мосту. В конструкції цієї інженерної споруди використані елементи у вигляді графіків відомих елементарних функцій: прямі лінії, параболи, гіперболи. Саме такі форми, за інженерними розрахунками, забезпечують міцність і надійність цієї споруди. Властивості функцій враховують при виготовлені дзеркал, прожекторів, шаблонів для виробництва деталей тощо.

Задача5.Опора має форму параболи. Складіть рівняння цієї параболи, якщо висота арки дорівнює 5м, а її найбільша ширина – 20м.(Відповідь:         у= -0,05)

Розвязання: Виберимо осі координат так, щоб вісь ОХ пройшла вздовж моста, а вісь ОУ – по осі симетрії параболи. Рівняння параболи у цій системі координат має вигляд у=а, де а<0 точка А(10;-5) – належить графіку функції, тому справедлива рівність -5=а∙, а звідси а=-0,05. Отже, рівняння параболи має вигляд у=-0,05

Задача6. Рух двох велосипедистів задано рівняннями:

 S₁ = 4 - t²,

 S₂= 3t.

1) Побудуйте графік руху кожного велосипедиста.

2) Знайдіть  час зустрічі велосипедистів.

 

Творчі завдання

На уроці ми працювали з параболою – графіком функції у=. Чи потрібно вивчати у школі дану функцію, чи використовуються її властивості в інших науках?

На мою думку вивчати  функції та їх властивості потрібно. Насамперед властивості функції використовують у фізиці, адже за їх допомогою можна змоделювати явища, які відбуваються в природі, на виробництві. Властивості функцій враховують при виготовлені дзеркал, прожекторів, шаблонів для виробництва деталей тощо.

Презентація «Парабола навколо нас»

Параболу можна використати у мистецтві. За допомогою графіків функцій можна  намалювати малюнок. Я побудувала ось такий малюнок.

   

 

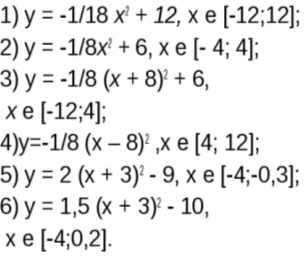
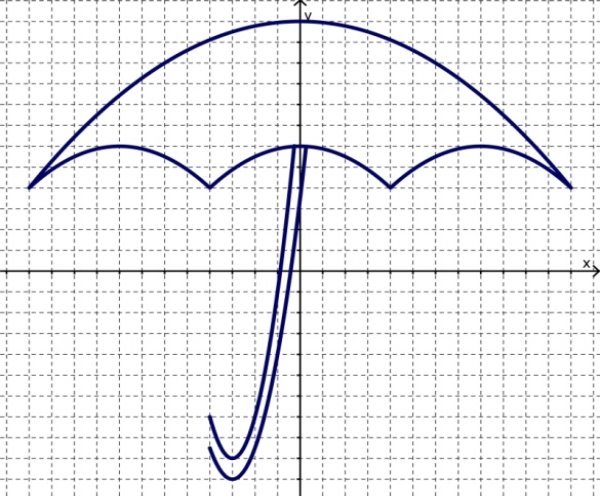
«Нехай ця парасолька захищає вас від всяких негараздів

 

    V. Підведення підсумків

Добре засвоєна мудрість не забувається ніколи.

                                                                            Піфагор

«Дерево знань»

Сьогодні на уроці ми вдосконалили навички розв’язування вправ на  дослідження функцій,  перетворення графіків функцій; ви здолали чергові сходинки до успіху. Чи розвязали ви поставлені на початку уроку завдання?

Було цікаво…

Було складно…

Тепер я знаю…

Я зрозумів, що…

Тепер я вмію….

                       Оцінювання знань учнів.

Корінь навчання гіркий, а плоди його солодкі.

                                                   Аристотель(давньогрецький філософ)

«Дерево знань»

 

Учні за нотатками у своїх аркушах оцінювання визначають загальну кількість набраних балів.

Намалюйте ескіз параболи і домалюйте обличчя, що передає ваш настрій. Це й буде ваша оцінка уроку.

 

VI. Домашнє завдання

        Як крапля довбає камінь не силою, а частим падінням, так і людина стає вченою частим учінням.

                                                              Фрідріх Дістервег (нім.педагог)

 

            п.9,10 № 404, №413, №414(4)

 

        VIІ.Рефлексія

Я дякую за активну роботу і співпрацю на уроці. Ви оцінили свою роботу в оцінному аркуші, і я впевнена, що ви це зробили відповідально. Ви вмієте застосовувати набуті знання, а це означає , що кожен із вас як і сьогодні , так і в майбутньому буде компетентний в певній галузі. Сподіваюся, знання, яких ви набули сьогодні, ще не раз стануть вам у пригоді.