Урок "Періодичність тригонометричних функцій"
Тема заняття: Періодичність тригонометричних функцій.
Мета заняття: ввести поняття періодичної функції, знаходження найменших додатних періодів тригонометричних функцій; розвивати пам'ять, логічне мислення, увагу; виховувати інтерес до предмету.
Тип заняття: лекція комплексного характеру.
Обладнання: підручники, мультимедійна презентація.
Література:
1. Алгебра і початки аналізу. Підручник для 10 кл. загальноосвітніх навчальних закладів, М.І. Шкіль, З.І. Слєпкань, О.С. Дубинчук. – К.: Зодіак – ЕКО, 2002, - 272 с.
2. Алгебра і початки аналізу: Підручник для 10-11 кл. загальноосвітніх навчальних закладів. – К.: Освіта, 2006. – 255с.
План заняття
І. Організація початку заняття.
ІІ. Актуалізація опорних знань.
- Перевірка домашнього завдання.
- Усне опитування.
ІІІ. Повідомлення теми, мети заняття.
IV. Вивчення нового матеріалу:
- Поняття періодичної функції.
- Найменші додатні періоди тригонометричних функцій.
V. Систематизація знань студентів.
VІ. Підведення підсумків заняття. Домашнє завдання.
Хід заняття
І. Організація початку заняття.
ІІ. Актуалізація опорних знань.
- Перевірка домашнього завдання.
Відповіді на запитання студентів, які виникли у них при розв’язуванні домашнього завдання.
- Усне опитування.
-
Що таке арккосинус числа? Властивості функції
 .
.
-
Що таке арксинус числа? Властивості функції
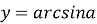 .
.
- Що таке арктангенс і арккотангенс числа?
ІІІ. Повідомлення теми, мети заняття.
IV. Вивчення нового матеріалу.
У природі часто зустрічаються явища, які повторюються періодично. Наприклад, Земля при обертанні навколо Сонця періодично повертається у своє початкове положення через рік, два роки, три роки і т. д., тому говорять, що період обертання Землі навколо Сонця дорівнює одному року. Періодичний характер мають рухи маховика і колінчатого вала. Властивість періодичності мають звукові, електромагнітні явища, робота серця людини і т. д. Закономірності періодичних явищ описуються періодичними функціями, до вивчення яких ми і приступаємо.
Функція ![]() називається періодичною з періодом
називається періодичною з періодом ![]() , якщо для будь-якого х із області визначення числа
, якщо для будь-якого х із області визначення числа ![]() і
і ![]() також належать області визначення і виконується рівність
також належать області визначення і виконується рівність ![]()
Так як одній і тій самій точці ![]() одиночного кола відповідає нескінченна множина дійсних чисел
одиночного кола відповідає нескінченна множина дійсних чисел ![]() , де
, де ![]() , то
, то
![]() ,
,
![]()
Звідси випливає, що ![]() - періоди функції синус і косинус
- періоди функції синус і косинус ![]() .
.
Доведемо, що число![]() є найменшим додатним періодом функції
є найменшим додатним періодом функції ![]() . Нехай
. Нехай ![]() - період косинуса, тобто для будь-якого
- період косинуса, тобто для будь-якого ![]() виконується нерівність
виконується нерівність ![]() . Взявши
. Взявши ![]() , одержимо
, одержимо ![]() . Звідси
. Звідси ![]() . Через те що
. Через те що ![]() , Т може дорівнювати
, Т може дорівнювати ![]() ... і тому період не може бути меншим
... і тому період не може бути меншим ![]() .
.
Можна довести, що найменший період функції ![]() теж дорівнює
теж дорівнює ![]() . Нехай Т — довільний період синуса. Тоді
. Нехай Т — довільний період синуса. Тоді ![]() для будь-якого
для будь-якого ![]() . Взявши
. Взявши ![]() , одержимо
, одержимо ![]() , але
, але ![]() , якщо
, якщо ![]() ,n
,n![]() Z, тому
Z, тому ![]() . Найменше додатне число виду
. Найменше додатне число виду ![]() є число
є число ![]() .
.
Доведемо, що найменшим додатним періодом функції ![]() є число
є число ![]() . Нехай Т — додатний період тангенса, тобто
. Нехай Т — додатний період тангенса, тобто ![]() . Взявши
. Взявши ![]() , маємо
, маємо ![]() . Звідси
. Звідси ![]() . Через те що найменше ціле додатнеп
. Через те що найменше ціле додатнеп![]() ,
, ![]() — найменший період функції
— найменший період функції ![]() . Найменшим додатним періодом котангенса теж є число
. Найменшим додатним періодом котангенса теж є число ![]() . Отже,
. Отже,
![]() ,
,
![]() .
.
Як правило, слова «найменший додатний період» опускають. Прийнято говорити, що період тангенса і котангенса дорівнює ![]() , aперіод косинуса і синуса дорівнює
, aперіод косинуса і синуса дорівнює ![]() .
.
Справедливе твердження.
Якщо функція ![]() періодична і має період Т, то функція
періодична і має період Т, то функція ![]() , де
, де ![]() — постійні
— постійні ![]() , також періодична, причому її період дорівнює
, також періодична, причому її період дорівнює ![]() .
.
Доведемо це твердження.
Спочатку доведемо, що ![]() є періодом функції
є періодом функції ![]() :
:
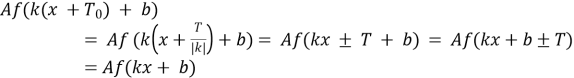 .
.
Нехай ![]() — період функції
— період функції ![]() , тобто
, тобто
![]() ,
,
![]() .
.
Позначивши ![]() маємо
маємо ![]() . Через те що найменшим періодом функції
. Через те що найменшим періодом функції ![]() , то
, то ![]() , звідси.
, звідси.
V. Систематизація знань студентів.
1. Обчисліть:
a) sin 1470°; б) tg 1860°; в) cos 1140°; г) ctg 1125°.
Відповідь: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() г)1.
г)1.
2. Знайдіть значення:
a) ![]() ; б)
; б) ![]() ; в)
; в)![]() ; г)
; г)![]() .
.
Відповідь: а)![]() ; б)
; б)![]() ; в)
; в)![]() ; г) 1.
; г) 1.
3. Знайдіть найменший додатний період функцій:
а)![]() ; б)y=3cos 4x;
; б)y=3cos 4x;
в)![]() ; г)
; г) ![]() .
.
Відповідь: а) π; б)![]() ; в)
; в)![]() ; г) 4π.
; г) 4π.
4. Знайдіть значення sin α, якщо:
a) sin (α + 2π) = 0,3; б) sin (4π - α)=0,2;
в) sin (α + 6π) = 0,5; г) sin (α – 2π) = 0,1.
Відповідь: а) 0,3; б)-0,2; в) 0,5; г) 0,1.
VІ. Підведення підсумків заняття. Домашнє завдання.
Розділ І § 5. Запитання і завдання для повторення до розділу 1 № 47—49. Вправа № 24 (1—3).


про публікацію авторської розробки
Додати розробку
