Конспект уроку з геометрії для 8 класу на тему " Теорема Піфагора". Презентація.

Конспект уроку з  геометрії для 8 класу

Тема  уроку: Теорема Піфагора.

Мета уроку:  узагальнити, систематизувати та закріпити знання учнів про теорему Піфагора, ознайомити з різними способами доведення цієї теореми; сформувати поняття єгипетського трикутника, піфагорової трійки чисел, піфагорових трикутників. Показати застосування набутих знань у практичній діяльності; розвивати вміння аналізувати, робити висновки.

Тип уроку: засвоєння нових знань.

Обладнання: презентація „ Теорема Піфагора”.

ХІД УРОКУ

Світ, що нас оточує, - це світ геометрії. Тож давайте його пізнавати!

І. Організаційний етап.

ІІ. Формулювання мети і завдань уроку.

     Вступне слово вчителя.

Теорема Піфагора – одна з основних у евклідовій геометрії. Завдяки їй можна довести більшість теорем геометрії та розв'язати не одну задачу. Тому її потрібно добре засвоїти. Сьогодні у нас урок однієї теореми, на якому ви познайомитеся з різними способами доведення теореми Піфагора ( відомо понад 100 різних доведень), використовуючи для цього знання з різних розділів планіметрії; розв'язувати задачі на застосування цієї теореми.

ІІІ. Перевірка домашнього завдання.

      Ви вдома готували усний журнал про математика, іменем якого названа ця теорема.

Презентація ( слайд 1)

1 учень. 

    Цього міцного юнака з товстою шиєю та коротким носом, справжнього забіяку, судді однієї з перших олімпіад не хотіли допускати до змагань, тому що Піфагор був малий на зріст. Але йому вдалося побитися зі своїми супротивниками та ще й перемогти. Якби це сталося якихось 2530 років поспіль, газети всього світу помістили б статтю з текстом „ Нікому невідомий Піфагор завоював медаль у кулачному бою”.

   За деякими даними, Піфагор народився близько 580 р. до н.е. у Стародавній Греції на острові Самос, а помер у 500 р. до н. е.

    Про життя вченого відомо небагато, але з його ім'ям пов'язаний ряд легенд. Розповідають, що він багато подорожував, був у Індії, Єгипті, Вавилоні, вивчав стародавню культуру й досягнення науки різних країн. Повернувшись на батьківщину, він організував гурток з молоді – представників аристократії. У гурток приймали з великими почестями після випробувань. Кожен, хто приходив у гурток, відмовлявся від свого майна й обіцяв зберігати в таємниці вчення засновника.

    Так на півдні Італії, що була на той час грецькою колонією, виникла так звана Піфагорійська школа. Ті, хто хотів потрапити до неї, повинні були мовчати протягом п'яти років, тільки після цього їх зараховували. Та, незважаючи на незвичайний і жорстокий іспит, багато хто прагнув потрапити до цієї школи.

  Піфагорійці займалися математикою, філософією, природничими науками. Вони багато винайшли в арифметиці й геометрії. У школі існував декрет. За яким авторство усіх математичних робіт присвоювалося Піфагору.

  За однією з версій він був убитий під час народного повстання.

    Після його смерті учні оточили ім'я свого вчителя різноманітними легендами. Тому встановити правду про звички й характер Піфагора неможливо.

2 учень.

    1. Піфагор першим з грецьких математиків вивчав пропорцію та найпростіші види прогресій: арифметичну, геометричну, гармонічну.

    2. Піфагор першим використав метод доведення від супротивного.

    3. Він створив елементарні принципи побудови правильних многогранників, які назвав космічними фігурами.

    4. Піфагор вважав, що куля найдосконаліша з усіх геометричних тіл і що Земля повинна мати форму кулі.

Презентація ( слайд 2)

3 учень. 

          Особливу увагу Піфагор приділяв числам.

           Він вважав, що число 5 символізує колір, 6 – холод, 7 – розум, 8 – кохання, дружбу, 9 – постійність, 13 і 14 були ненависними числами.

         Парні числа вважалися нещасливими, а непарні – щасливими. Чи збереглася ця піфагорійська традиція зараз і де?  ( Так, вважається, що треба дарувати букет з непарною кількістю квіток).

 Ірраціональні  числа також відкрив Піфагор, шукаючи діагональ квадрата зі стороною 1.

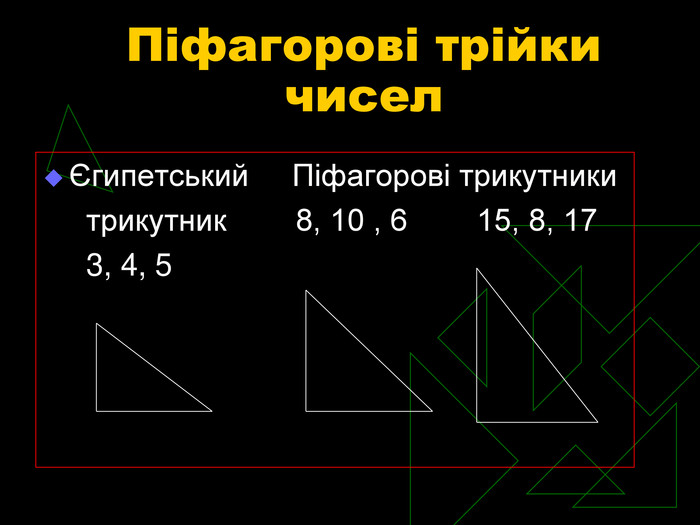
Також серед чисел виділяють піфагорові трійки чисел. Це трійки чисел, що задовольняють рівняння виду a² + b² =  c² , де а, b, с – взаємно прості числа.

3, 4, 5; 5, 12, 13; 15, 8, 17.

Знання піфагорових трійок  може допомогти спростити обчислення невідомих сторін трикутників.

4 учень

 Землеміри Стародавнього Єгипту для побудови прямого кута користувалися таким способом. Мотузку ділили вузлами на 12 рівних частин і кінці зв'язували. Потім її розкладали на землі так, щоб утворився трикутник зі сторонами 3, 4, 5 поділок. Кут трикутника, протилежний стороні, що має 5 поділок, - прямий. Тому прямокутний трикутник зі сторонами 3, 4, 5 одиниць називають єгипетським, або піфагоровим.

Презентація ( слайд 3)

( Один учень біля дошки доводить теорему Піфагора за вивченим на попередньому уроці).

Запитання до класу:

1. Який трикутник називають прямокутним?

2. Які сторони в прямокутному трикутнику називаються катетами?

3. Як називається найбільша сторона прямокутного трикутника?

4. Проти якого кута лежить гіпотенуза прямокутного трикутника?

5. У прямокутному трикутнику будь – який з катетів завжди менший за .........

Слово вчителя:

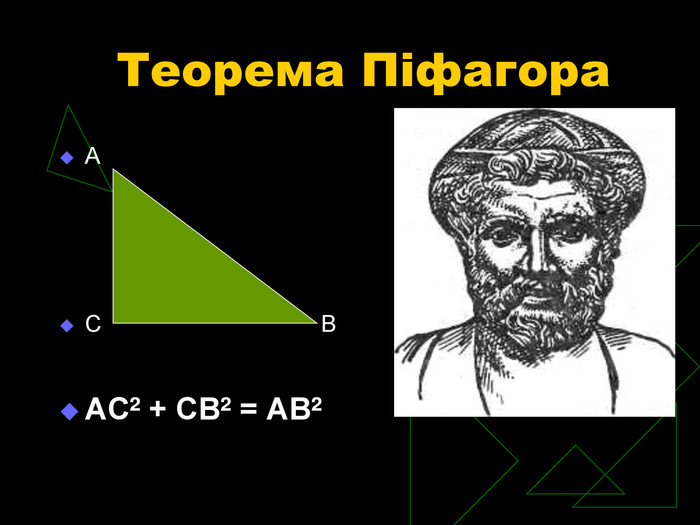
   Теорема Піфагора має багату історію. Ще задовго до Піфагора вона була відома єгиптянам, вавілонянам, китайцям та індійцям. Доведення самого Піфагора до нас не дійшло. В наш час є більше 100 різних доведень теореми Піфагора. Можливо, що одне з них належить Піфагору чи його учням.

Презентація ( слайд 4)

ІV   Різні доведення теореми Піфагора

Теорема Піфагора чудова тим, що вона зовсім не очевидна. Із простого споглядання прямокутного трикутника не зробиш висновок, що між його сторонами є таке просте співвідношення a² + b² =  c². Але це співвідношення стає очевидним, якщо вдало побудувати малюнок.

1. Давньоіндійське доведення

 У книзі „ Вінок знання” індійський математик Бхаскара наводить доведення теореми Піфагора у вигляді креслення з підписом „Дивись!” Як дістати з креслення Бхаскара доведення теореми Піфагора?

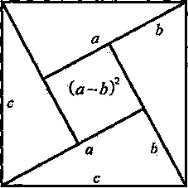
Площа квадрата, побудованого на гіпотенузі с трикутника, дорівнює сумі площ чотирьох прямокутних трикутників і квадрата, довжина сторони якого a – b. Тобто

                c²= 4 · + ( а – b)² = 2 аb +  а² - 2ab + b² = a²  + b².

Отже, c² = a² + b².

Оскільки квадрати відрізків а, b, c дорівнюють площам квадратів з такими сторонами, то теорему Піфагора часто формулюють і так:

    Площа квадрат, побудованого на гіпотенузі прямокутного трикутника, дорівнює сумі площ квадратів, побудованих на його катетах.

Презентація ( слайд 5 )

Презентація ( слайд 6 )

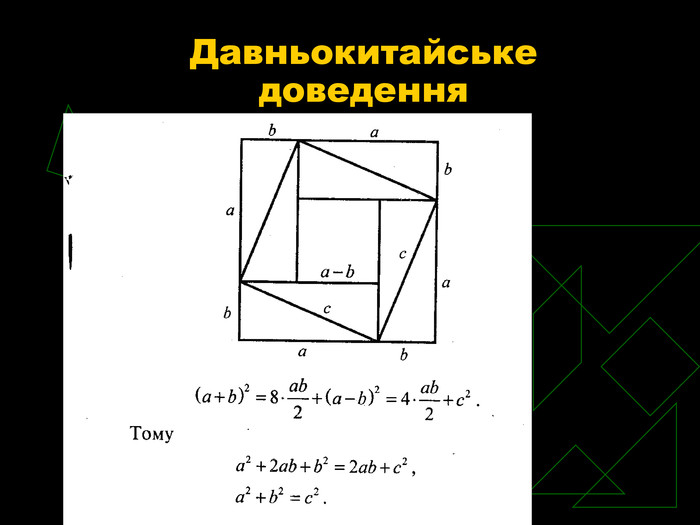
2. Давньокитайське доведення

У коментарі до задачі з „ Трактату про мірну віху” є посилання на креслення, де квадрат, побудований на сумі катетів а і b прямокутного трикутника, подано як суму площ інших фігур.

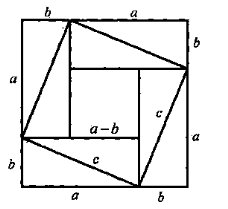
(a + b)² = 8· + (a - b)² = 4· + c²

                    тому a² + 2ab + b² = 2ab + c²,

                                       c² = a² + b².

3. Наочне ілюстрування теореми Піфагора – зважування.

      Якщо вирізати з картону три квадрати, сторони яких дорівнюють сторонам даного трикутника, і покласти два менших квадрати на одну шальку досить чутливих терезів, а на другу шальку – третій, то терези будуть у рівновазі.

Ще відомими у шкільному курсі геометрії є векторний метод доведення та метод координат. Із цими способами ми познайомимося , вивчаючи далі в старших класах курс геометрії.

V.  Розв'язування задач.

        Учні із середнім рівнем знань виконують завдання з дошки.

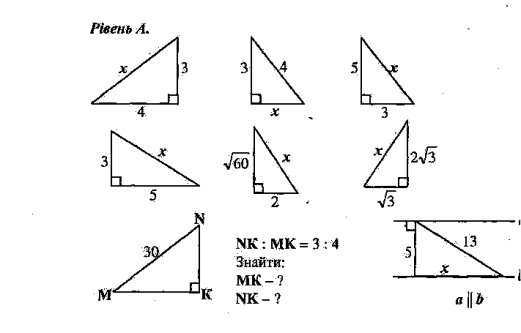
      Учні з достатнім та високим рівнем знань виконують номери  з підручника:  №

VІ . Підсумок уроку

Математична вікторина

1. У якому столітті жив Піфагор ? (VІ ст. до н. е.)

2. Що ви можете сказати про множину ірраціональних чисел? ( Цей вид чисел відкрив Піфагор, шукаючи діагональ квадрата зі стороною 1).

3. Який трикутник називають єгипетським? ( із сторонами 3, 4, 5 ).

4. Сформулюйте теорему Піфагора.

VІІ. Домашнє завдання

        Вивчити зміст основних понять уроку.

         Виконати № 42, 51.