Урок «Перпендикулярність прямих і площин у просторі»

Контрольна робота. Варіант 1.

«Перпендикулярність прямих і площин у просторі»

1. Точка К знаходиться на відстані 4 см від кожної з вершин правильного трикутника АВС. Знайдіть довжину сторони трикутника, якщо точка К віддалена від площини АВС на 2 см.

2. З точки В до площини γ  проведено перпендикуляр ВО і похилі ВА і ВС. Відомо, що ОА = 12 см, ОС = 30 см,  а довжини похилих  відносяться як 10 : 17. Знайдіть довжину  похилої ВА .

3. Кінці відрізка АВ належать двом перпендикулярним площинам α і β. Проекція відрізка АВ на площину α дорівнює 5 см, а його проекція на площину  β  дорівнює 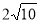см.  Відстань між основами перпендикулярів, опущених з кінців відрізка АВ на лінію перетину площин, дорівнює 4 см. Знайдіть довжину відрізка АВ.

4.  Точка Р рівновіддалена від сторін ромба АВСD і знаходиться на відстані 8 см від його площини. Знайдіть відстань від точки Р до сторін ромба, якщо висота ромба дорівнює 12 см.

Контрольна робота. Варіант 2.

«Перпендикулярність прямих і площин у просторі»

1. Точка  М  знаходиться на відстані 8 см від кожної з вершин  квадрата  АВСD. Знайдіть довжину сторони  квадрата, якщо точка  М віддалена від його  площини  на 4 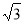см.

2. З точки А до площини α  проведено перпендикуляр АО і похилі АВ і АС, причому похила АВ на 4 см менша від похилої АС. Проекції даних похилих на площину α дорівнюють 1 см і 7 см. Знайдіть відстань від точки А до площини α.

3. Кінці відрізка, довжина якого дорівнює 10 см, належать двом перпендикулярним площинам. Кути між даним відрізком і цими площинами дорівнюють 45° і 30°. Знайдіть відстань між основами перпендикулярів, опущених з кінців відрізка на лінію перетину площин.

4.  Сторона правильного трикутника дорівнює 6 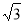см. Точка М рівновіддалена від сторін трикутника і знаходиться на відстані  6 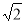см від його площини. Знайдіть відстань від точки М до сторін трикутника.