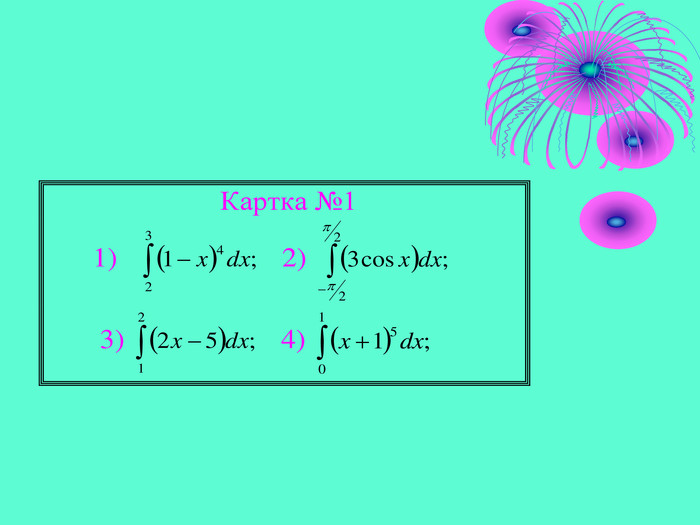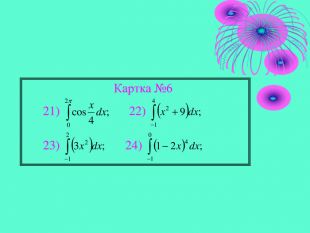Первісна, інтеграл (Урок, Презентація, Тести)
Перевірка рівеня оволодіння учнями вивченого матеріалу з даної теми, реалізація отриманих знань при виконанні завдань різного рівня складності.
Урок – залік проводиться у формі гри. Клас ділиться на чотири команди.
- ,інтеграл.doc doc
- .ppt ppt
- .xls xls
- _тести.doc doc
Урок. «Первісна і інтеграл».
Мета уроку: перевірити рівень оволодіння учнями вивченого матеріалу з даної теми, сприяти реалізації отриманих знань при виконанні завдань різного рівня складності, формувати у учнів таких рис, як відчуття взаємовідповідальності і самоствердження, самоаналізу і самооцінки.
Хід уроку.
1. Організаційний момент.
Урок – залік проводиться у формі гри. Клас ділиться на чотири команди. Вибирається капітан (до початку заняття). Команди сідають за свої столи. На столі кожної команди лежить «Лист обліку знань», де капітан навпроти кожного прізвища ставить (у разі правильної відповіді) знак «+».
За підсумками кожного туру підраховуються знаки «+» і в рядку «всього» ставиться їх кількість за команду. у рядку навпроти прізвища підсумовуються знаки «+» і можна виставити оцінку кожному за роботу на уроці.
Лист обліку знань.
|
№ |
Прізвище Ім'я |
Тури |
Сума плюсів |
Оцінка за урок. |
||||
|
1 |
2 |
3 |
4 |
5 |
||||
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
Всього |
|
|
|
|
|
|
|
1 Тур «Розминка».
Відгадування кросворду. Тут учні повинні показати свої теоретичні знання на мінімальному рівні. Кросворд пишеться на окремих листах і видається кожній команді. За кожне правильно вгадане слово команда отримує 1 бал. Це завдання на швидкість, і команда, яка перша відгадала кросворд, отримує додатково 4 бали.
Максимальна кількість балів, яку може отримати команда, дорівнює 16.Час виконання завдання 10 хвилин.
У листі обліку знань ставиться в рядку «Всього» число балів, одержаних командою. Цей результат заноситься в таблицю на дошці.
-
Як називається функція
 ?
?
-
Що є графіком функції
 ?
?
- Найнижчий шкільний бал?
- Який урок зазвичай проходить перед заліком?
- Синонім слова дюжина?
- Є в кожному слові, у рослини і може бути у рівняння?
- Що можна обчислити за допомогою інтегралу?
- Одне з найважливіших понять математики.
- Форма уроку, на якому проводиться перевірка знань.
- Німецький учений, на честь якого названа формула, що зв'язує площу криволінійної трапеції і інтеграл.
-
Множина точок площини з координатами
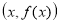 , де
, де  пробігає область визначення функції
пробігає область визначення функції  .
.
-
Відповідність між множинами
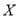 і
і 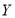 при якому кожному значенню множини
при якому кожному значенню множини 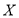 поставлено у відповідність єдине значення з множини
поставлено у відповідність єдине значення з множини 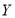 носить назву...
носить назву...
ВІДПОВІДІ: 1. Первісна. 2. Пряма. 3. Одиниця. 4. Контрольна. 5. Дванадцять. 6. Корінь. 7. Площа. 8. Інтеграл. 9. Залік. 10. Лейбніц. 11. Графік. 12. Функція.
2 Тур «Далі, далі...»
Цей гейм індивідуальний, тобто кожен учень пише відповіді в своєму зошиті. Час виконання завдання 15 хвилин. Після закінчення цього часу вчитель зачитує відповіді. Учні у себе в зошитах обводять правильну відповідь в кружок і підраховують кількість кружків (стільки плюсів ставлять капітани команд в «Лист обліку знань»), і кожен отримує оцінку за цей етап. Капітани команд підраховують середній бал і повідомляють викладача, який ставить ці дані в табло.
- Що називається первісною?
- Як читається основне правило первісної?
- Як можна обчислити площу криволінійної трапеції за допомогою інтеграла?
- Запишіть з допомогою інтеграл площу фігури зображеної на малюнку:
-
Знайти первісні для функцій: а)
 б)
б) в)
в) г)
г) д)
д)  е)
е) 
- Чи істинні рівності:
 а)
а)  б)
б) 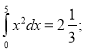 в)
в) 
г) 
д) 
е) 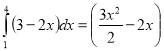 ?
?
ВІДПОВІДІ:
1) Функція ![]() називається первісною для функції
називається первісною для функції ![]() на заданому проміжку, якщо для всіх
на заданому проміжку, якщо для всіх ![]() з цього проміжку
з цього проміжку ![]() .
.
2) Будь-яка первісна для функції ![]() на проміжку може бути записана у вигляді
на проміжку може бути записана у вигляді ![]() , де
, де ![]() - одна з первісних для функції
- одна з первісних для функції ![]() на заданому проміжку, а
на заданому проміжку, а ![]() - довільна стала.
- довільна стала.
3) 
4) 
5) а) ![]() б)
б) ![]() в)
в) ![]() г)
г)![]() д)
д)![]() е)
е)![]()
6) а) істинне; б) помилкове; у) помилкове; г) помилкове; д) істинне; е) помилкове.
3 Тур «Поспішіть побачити».
Кожна команда отримує картку із завданням. Перша і третя команди отримують однакові картки, друга і четверта теж. Це завдання на швидкість і воно виконується на окремих листах. Час виконання 10 хвилин. Команда, що перша виконала завдання, отримує 1 додатковий бал. За правильне виконання завдання команда отримує 1 бал. У завданні потрібно зобразити криволінійну трапецію, обмежену:
а) графіком функції ![]() і прямій
і прямій ![]()
б) графіком функції ![]() віссю ОХ і прямій
віссю ОХ і прямій ![]()
ВІДПОВІДІ:
|
а) |
|
б) |
4 Тур «Складіть фразу».
Кожній команді видається 7 карток, на кожній з яких написано по 4 інтеграл. Завдання команди обчислити всі 28 інтегралів; знайти на дошці правильну відповідь, під якою записана буква. Зіставивши результат обчислення інтеграла і букву, учні повинні отримати фразу. Команда, яка перша відгадає фразу, отримує додатковий бал. Бали нараховуються команді за кожну правильно знайдену букву. Час виконання завдання 20 хвилин.
Обчислити інтеграли.
1) 
2) 
3) 
4) 
5) 
6) 
7) 
8) 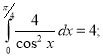
9) 
10) 
11) 
12) 
13) 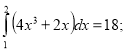
14) 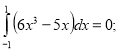
15) 
16) 
17) 
18) 
19) 
20) 
21) 
22) 
23) 
24) 
25) 
26) 
27) 
28) 
ВІДПОВІДІ:
|
9 – |
27 – |
17 – |
7 – |
|
16 – 2 |
О – 4 |
2,6 – 6 |
1 – 6,2 |
|
8,21,25 – 0 |
3 – (- 2) |
5,23 – 9 |
4 – 10,5 |
|
10,13,15 – 18 |
24 – 24,2 |
Л – 48 |
18 – 63,75 |
В результаті повинно вийти:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 Тур «Гонка за лідером».
Кожна команда отримує картку. Перша і третя команди отримують картку 1, друга і четверта команди отримують картку 2. У кожній картці по два завдання: одне у формі тесту, інше – своєрідний кросворд.
За перше правильно вирішене завдання команда отримує 1 бал, за друге – 3 бали. Час виконання завдання 20 хвилин.
Картка 1.
Завдання 1.
Для функції ![]() знайти первісну, графік якої проходить через точку М(4; 5).
знайти первісну, графік якої проходить через точку М(4; 5).
А)![]() Б)
Б)![]() В)
В)![]() Г)
Г)![]() ВІДПОВІДЬ: Б.
ВІДПОВІДЬ: Б.
 Завдання 2.
Завдання 2.
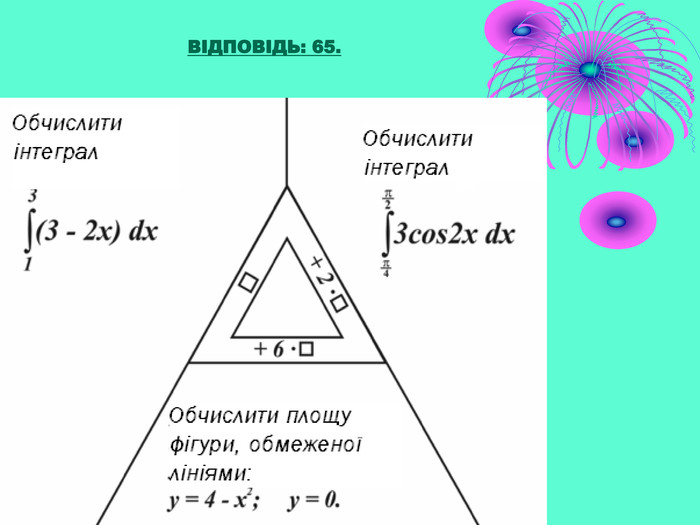
ВІДПОВІДЬ: 65.
Картка 2.
Завдання 1.
Для функції ![]() знайти первісну, графік якої проходить через точку М(1; 3).
знайти первісну, графік якої проходить через точку М(1; 3).
А)![]() Б)
Б) ![]() В)
В) ![]() Г)
Г)![]() ВІДПОВІДЬ: В.
ВІДПОВІДЬ: В.
Завдання 2.
 ВІДПОВІДЬ: 28.
ВІДПОВІДЬ: 28.
Підведення підсумків
На табло підраховуються бали, отримані кожною командою, і розподіляються місця. Кожен учасник команди, яка зайняла 1 місце отримує оцінку «12». Окрім цього, все учні отримують оцінку за індивідуальне завдання і за роботу в колективі.
Кожна команда повинна відповісти на наступні запитання:
1. Що вам сподобався урок такого роду?
2. Яка мета була досягнута на цьому уроці?
3. Що вам не сподобалося і що б ви змінили?
Тест по варіантах.
Варіант 1.
-
Обчислити

а) 27; б) 24; у) 18; г) 21.
-
Знайдіть

а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г) інтеграл не існує.
; г) інтеграл не існує.
-
Обчислити

а) - 2; б) 2; у) - 3; г) 3.
-
Обчислити

а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
-
При якому значенні
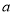 виконується рівність
виконується рівність  ?
?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
-
Обчислити площу фігури, обмеженій графіком функції
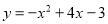 і прямою
і прямою
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
-
Обчислити площу фігури, обмеженою графіком функції
 дотичною до параболи в точці
дотичною до параболи в точці  і прямою
і прямою 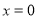
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
-
 Обчислити площу фігури, обмеженої графіками функцій
Обчислити площу фігури, обмеженої графіками функцій 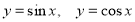 і прямими
і прямими  .
.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
-
Знайдіть

а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
-
Графік функції
 перетинає графік своєї первісної
перетинає графік своєї первісної  у двох точках, одна з яких (-1;-4). Знайдіть площу фігури, обмеженої графіками
у двох точках, одна з яких (-1;-4). Знайдіть площу фігури, обмеженої графіками 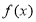 і
і  .
.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
Варіант 2.
-
Обчислити

а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
-
Знайдіть

а) 0; б) -12; у) інтеграл не існує; г) 12.
-
Обчислити

а) – 3,5; би) 4,5; у) – 4,5; г) 3,5.
-
Обчислити

а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
-
При якому значенні
 виконується рівність
виконується рівність 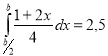 ?
?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
-
Обчислити площу фігури, обмеженою графіком функції
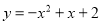 і пряміою
і пряміою
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
-
Обчислити площу фігури, обмеженою графіком функції
 дотичною до параболи в точці
дотичною до параболи в точці  і прямій
і прямій 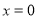
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
-
 Обчислити площу фігури, обмеженою графіками функцій
Обчислити площу фігури, обмеженою графіками функцій 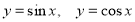 і прямими
і прямими  .
.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
-
Знайдіть

а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
-
Графік функції
 перетинає графік своєї первісної
перетинає графік своєї первісної  у двох точках, одна з яких (3;6). Знайдіть площу фігури, обмеженої графіками
у двох точках, одна з яких (3;6). Знайдіть площу фігури, обмеженої графіками 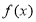 і
і  .
.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
ВІДПОВІДІ:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
Г |
Г |
В |
А |
Б |
А |
В |
Г |
Г |
Б |
|
2 |
Б |
В |
В |
Г |
Б |
Г |
А |
Б |
В |
А |
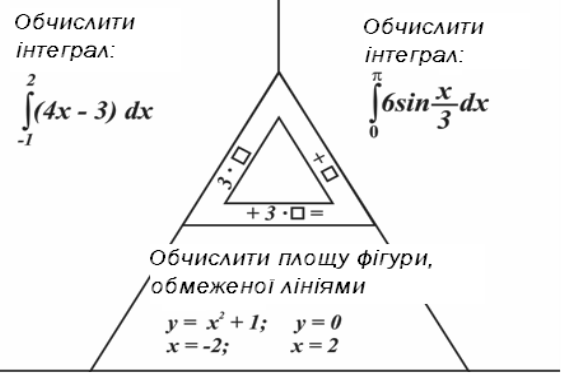

Картка №1
1)  2)
2)  3)
3)  4)
4) 
Картка №2
5) ![]() 6)
6)  7)
7)  8)
8) 
Картка №3
9)  10)
10)  11)
11) 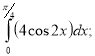 12)
12) 
Картка №4
13)  14)
14)  15)
15)  16)
16) 
Картка №5
17)  18)
18) ![]() 19)
19)  20)
20) 
Картка №6
21)  22)
22)  23)
23) 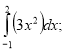 24)
24) 
Картка №7
25) ![]() 26)
26)  27)
27) ![]() 28)
28) 
Інтеграл – електронне тестування (Excel)
1.Знайдіть загальний вигляд первісної функції f(x)=3x²
А)3x³+ C ; В) х²+С;
Б) х³+С; Г) 6х +С.
2. Обчисліть інтеграл 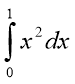 .
.
А) -![]() ; В) -
; В) -![]() ;
;
Б) ![]() ; Г)
; Г) ![]() .
.
3. Обчисліть інтеграл 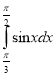
А) 1,5; В) -1,5;
Б) 0,5; Г) -0,5.
4. Обчисліть площу заштрихованої фігури зображеної на рисунку.
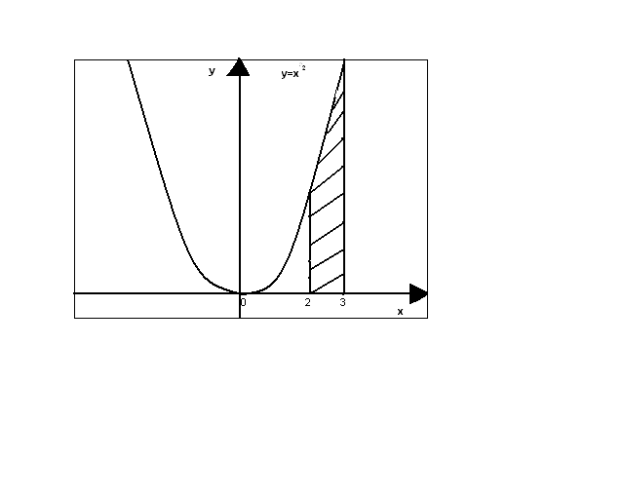
А) 19; В) 10![]() ;
;
Б) 6![]() ; Г) 1
; Г) 1![]() .
.
5. Яка з наведених функцій є первісною функції f(x)=x⁴?
А) F(x)=4x³; В) F (х)=![]() ;
;
Б) F(х)=![]() ; Г) F (х)=
; Г) F (х)=![]() .
.
6. Обчисліть інтеграл ![]() .
.
А) 15; В) -15;
Б) 30; Г) -30.
7. Укажіть первісну функції f(x)=sinx, графік якої проходить через точку В(![]() ; -2).
; -2).
А) F (x)= -cosx+1; В) F (x)= сosx-2;
Б) F (x)= -cosx-3; Г) ) F (x)= -cosx-2.
8. На рисунку зображено графіки функцій у=f(x) і y=g(х). Порівняйте значення виразів  і
і  .
.

А)  >
>  ; В)
; В)  =
=  ;
;
Б)  <
<  ; Г)Порівняти неможливо
; Г)Порівняти неможливо
9. Обчисліть інтеграл ![]() .
.
А)![]() ; В) -
; В) -![]() ;
;
Б)![]() ; Г) -
; Г) -![]() .
.
10. Яка з наведених функцій є первісною функції f(x)=3x2+4х ?
А) F(x)=x³+2х2+С; В) F (х)=6х+4+С;
Б) F(x)=x³+2х2; Г) F (х)= 3x³+4х2+С .
11. Обчисліть площу заштрихованої фігури, зображеної на рисунку
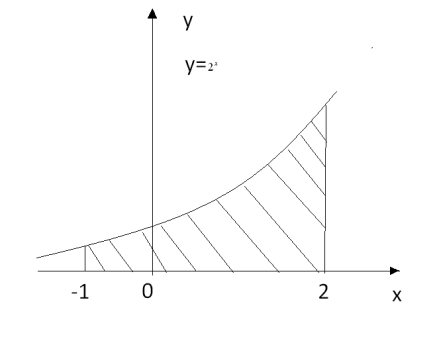
А)![]() ; В)
; В) ![]() ;
;
Б)![]() ; Г)
; Г) ![]() .
.
12. Обчисліть площу заштрихованої фігури, зображеної на рисунку

А)1; В) ![]() ;
;
Б)![]() ; Г)
; Г) ![]() .
.
Інтеграл
1.Знайдіть загальний вигляд первісної функції f(x)=3x²
А)3x³+ C ; В) х²+С; Б) х³+С; Г) 6х +С.
2. Обчисліть інтеграл  .
.
А) -![]() ; В) -
; В) -![]() ; Б)
; Б) ![]() ; Г)
; Г) ![]() .
.
3. Обчисліть інтеграл 
А) 1,5; В) -1,5; Б) 0,5; Г) -0,5.
4. Обчисліть площу заштрихованої фігури зображеної на рисунку.
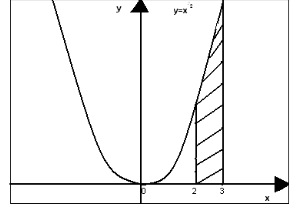
А) 19; В) 10![]() ; Б) 6
; Б) 6![]() ; Г) 1
; Г) 1![]() .
.
5. Яка з наведених функцій є первісною функції f(x)=x⁴?
А) F(x)=4x³; В) F (х)=![]() ; Б) F(х)=
; Б) F(х)=![]() ; Г) F (х)=
; Г) F (х)=![]() .
.
6. Обчисліть інтеграл ![]() .
.
А) 15; В) -15; Б) 30; Г) -30.
7. Укажіть первісну функції f(x)=sinx, графік якої проходить через точку В(![]() ; -2).
; -2).
А) F (x)= -cosx+1; В) F (x)= сosx-2; Б) F (x)= -cosx-3; Г) F (x)= -cosx-2.
8. На рисунку зображено графіки функцій у=f(x) і y=g(х). Порівняйте значення виразів  і
і  .
.

А)  >
>  ; В)
; В)  =
=  ;
;
Б)  <
<  ; Г)Порівняти неможливо
; Г)Порівняти неможливо
9. Обчисліть інтеграл ![]() .
.
А)![]() ; В) -
; В) -![]() ; Б)
; Б)![]() ; Г) -
; Г) -![]() .
.
10. Яка з наведених функцій є первісною функції f(x)=3x2+4х ?
А) F(x)=x³+2х2+С; В) F (х)=6х+4+С; Б) F(x)=x³+2х2; Г) F (х)= 3x³+4х2+С .
11. Обчисліть площу заштрихованої фігури, зображеної на рисунку

А)![]() ; В)
; В) ![]() ; Б)
; Б)![]() ; Г)
; Г) ![]() .
.
12. Обчисліть площу заштрихованої фігури, зображеної на рисунку

А)1; В) ![]() ; Б)
; Б)![]() ; Г)
; Г) ![]() .
.


про публікацію авторської розробки
Додати розробку





























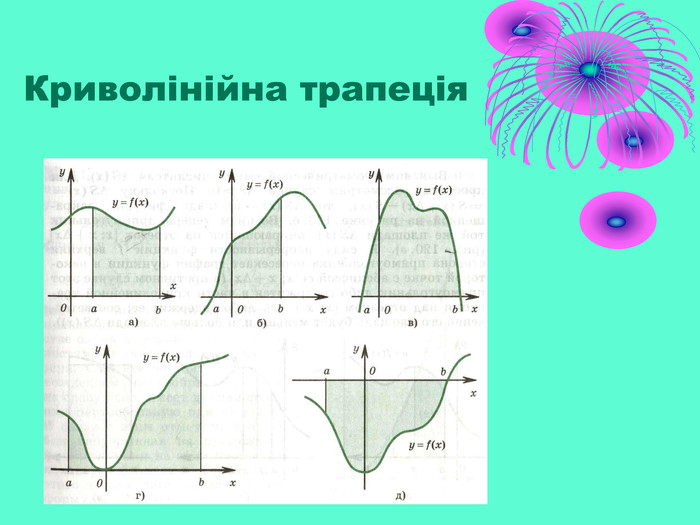
![Означення Криволінійною трапецією називається фігура, яка обмежена графіком додатньої і неперервної на відрізку [a;b] функції f, віссю Ox і прямими x = a і x = b. Означення Криволінійною трапецією називається фігура, яка обмежена графіком додатньої і неперервної на відрізку [a;b] функції f, віссю Ox і прямими x = a і x = b.](/uploads/files/33365/50806/53755_images/27.jpg)
![Математична модель 1) разбивають відрізок [a,b] на n рівних частин 2) Sn= f (Хo)ΔXo+ f (X1)ΔX1+ f (X2)ΔX2+…+ f (Xk)ΔXk+…+ f (Xn-1)ΔXn-1 3) обчислюють limSn n→∞ Математична модель 1) разбивають відрізок [a,b] на n рівних частин 2) Sn= f (Хo)ΔXo+ f (X1)ΔX1+ f (X2)ΔX2+…+ f (Xk)ΔXk+…+ f (Xn-1)ΔXn-1 3) обчислюють limSn n→∞](/uploads/files/33365/50806/53755_images/29.jpg)

![Теорема Якщо f-неперервна і додатня на [a,b] функція, а функція F – її первісна на цьому відрізку, то площа S відповідної криволінійної трапеції дорівнює приросту первісної на відрізку [a,b], тобто. S=F(b)-F(a) Теорема Якщо f-неперервна і додатня на [a,b] функція, а функція F – її первісна на цьому відрізку, то площа S відповідної криволінійної трапеції дорівнює приросту первісної на відрізку [a,b], тобто. S=F(b)-F(a)](/uploads/files/33365/50806/53755_images/31.jpg)
![ОЗНАЧЕННЯ ІНТЕГРАЛУ Інтегралом функції f(x)від a до b називається число, до якого прямує S(n) при n до нескінченності для будь-якої непрервної на відрізку [a;b] функції f(x). ОЗНАЧЕННЯ ІНТЕГРАЛУ Інтегралом функції f(x)від a до b називається число, до якого прямує S(n) при n до нескінченності для будь-якої непрервної на відрізку [a;b] функції f(x).](/uploads/files/33365/50806/53755_images/32.jpg)