Тема уроку. Пряма і правильна призми. Площі бічної і повної поверхні призми.

Мета уроку:   формування понять пряма, похила і правильна призми; вивчення теореми про бічну поверхню прямої призми.

Обладнання: моделі призми, схема «Види призм».

І. Перевірка домашнього завдання

1. Один учень відтворює на дошці розв'язування задачі № 10, решта відповідає на питання, а потім пише математичний диктант.
2. Фронтальне опитування.

1)Що таке переріз призми січною площиною?

  2) Якою фігурою є переріз призми площиною, паралельною бічним ребрам? Чому?

  3) Що таке діагональний переріз призми?

4) Якою фігурою є діагональний переріз призми? Чому?

5) Якою фігурою є переріз призми площиною, яка паралельна осно­вам? Чому?

3. Математичний диктант.

Побудуйте схематичне зображення чотирикутної призми, в якій бічні ребра перпендикулярні до основи й дорівнюють 10 см, а в основі лежить:

варіант 1 — прямокутник зі сторонами 6 см і 8 см;

варіант 2 — ромб з діагоналями 6 см і 8 см. (2 бали)

1) Знайдіть площі діагональних перерізів побудованої призми. (2 бали)

2) Побудуйте переріз, який проходить через сторону нижньої основи і протилежну сторону верхньої основи. (2 бали)

3) Якою фігурою є побудований переріз? (2 бали)

4) Чому дорівнюють сусідні сторони перерізів? (2 бали)

5) Знайдіть площу одержаного перерізу. (2 бали)

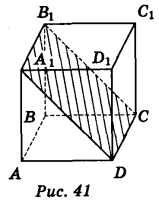
Відповідь. Варіант 1. Рис. 41; 1) 100 см² і 100 см²; 2) рис. 41; 3) прямокутник; 4) 8 см і 2см або 6 см і 2см; 5) 16см² або 12см².

Варіант 2. Рис. 41; 1) 60 см² і 80 см²; 2) рис. 41; 3) паралелограм; 4) 5см і 5см; 5) 25 см².

4. Заслухати учня, який відтворював розв'язання задачі № 10 та від­повісти на запитання, які виникли в учнів.

II. Сприйняття та усвідомлення нового матеріалу

Види призм

У стереометрії розглядають прямі і похилі призми (див. схему).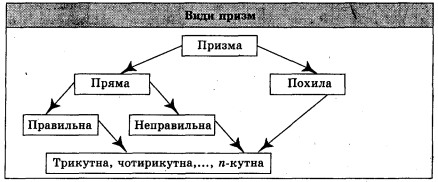 

Призма називається прямою, якщо її бічні ребра перпендикуляр­ні до основи.

Інші призми називаються похилими. Демонструються моделі прямих і похилих призм.

Пряма призма називається правильною, якщо в її основі лежить правильний многокутник. Демонструються моделі правильних призм.

Розв'язування задач

1. Якою фігурою є бічні грані прямої призми?

2. Доведіть, що якщо одне бічне ребро призми перпендикулярне до ос­нови призми, то призма є прямою.

3. Доведіть, що в прямій призмі бічне ребро перпендикулярне до діа­гоналей основи.

4. Якою фігурою є діагональний переріз прямої призми?

5. Доведіть, що якщо в призмі дві сусідні бічні грані перпендикулярні до площини основи, то призма пряма.

6. Доведіть, що у правильній призмі бічні грані рівні між собою.

7. Основою трикутної призми є рівносторонній трикутник. Одна із біч­них граней є прямокутником, який перпендикулярний до основи. Чи буде ця призма прямою? (Відповідь. Так.)

8. Задача № 17 (с. 78).

9. Задача № 15 (с. 77).

Якщо дозволяє час, можна показати учням два способи розв'язання цієї задачі.

Розв'язання

І спосіб

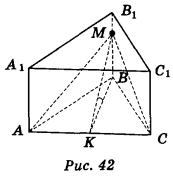
Нехай х — шуканий кут, а — сторона основи призми, S — площа осно­ви, S_пер — площа перерізу. Оскільки переріз проектується на основу, то  S = S_пер cos х, звідси cos х = . Оскільки ΔАМС (рис. 42) рівнобедрений, то, провівши     ВК AC, маємо: АК = КС = , <ΑΜΚ = <KMC = .

Із ΔΑΜΚ  MK=AKctg<AMK= .  Тоді , .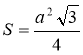

Отже. .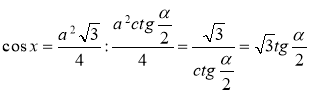

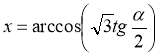
Відповідь. .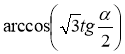

ІІ спосіб

Провівши KB AC, маємо АК = KC, <AMK = <KMC = . Нехай AC = a. 

Із ΔΑΜΚ MK = АК ctg <AMK = .

Із ΔΑΒK KB = AB sin<BAK = a sin 60° = .

Із ΔKΜΒ .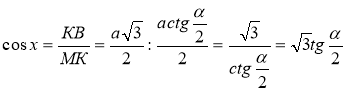

Тоді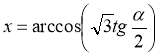

Відповідь. .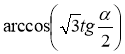

10. Задача № 14* (с. 77).

11. Задача № 12* (с. 77).

Поняття бічної і повної поверхні призми, теореми про бічну поверхню прямої призми.

Площею бічної поверхні (бічною поверхнею) призми називаєть­ся сума площ бічних граней. Повна поверхня призми дорівнює сумі бічної поверхні і площ основ: S_пр = S_біч + 2S_осн

Розв'язування задач

1. Основа прямої призми — прямокутний трикутник з катетами З і 4 см, висота призми 5 см. Знайдіть площу повної поверхні призми. (Відповідь. 72 см².)
2. Задача № 20 (с. 78).
3. У похилій трикутній призмі відстані між бічними ребрами дорів­нюють 5, 12, 9 см. Знайти бічне ребро призми, якщо бічна поверх­ня її дорівнює 260 см². (Відповідь. 10 см.)

Далі учні самостійно знайомляться з теоремою 5.1 про бічну поверх­ню прямої призми в п. 42 § 5 підручника.

Далі можна розв'язати фронтально задачу № 24 (1; 3) (с. 78).

III. Домашнє завдання

§ 5, π. 42; контрольні запитання № 15—18; задачі № 13, 21, 24 (2) (с. 77—78).

IV. Підведення підсумку уроку

Запитання до класу

1) Дайте означення прямої (похилої) призми.

2). Дайте означення правильної призми.

3) Перелічіть властивості прямої призми.

4) Перелічіть властивості правильної призми.

5) Що таке бічна поверхня призми (повна поверхня призми)?

6) Чому дорівнює бічна поверхня прямої призми?

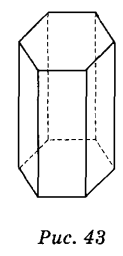
7) Дано пряму шестикутну призму (рис. 43). Укажіть, які із наведе­них тверджень правильні, а які — неправильні:

а) всі бічні грані призми — рівні прямокутники;

б) всі бічні грані — прямокутники;

в) висота призми дорівнює бічному ребру;

г) всі діагональні перерізи рівні.

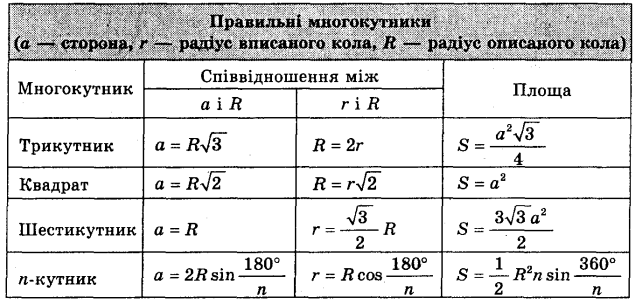
На цьому і на наступних уроках можна використовувати довідкову схему «Правильні многокутники».