Урок "Площа паралелограма і трикутника"

Площа паралелограма і трикутника

Дидактична мета: поглибити знання учнів з теми про площі многокутників, розглянути і довести формули площі паралелограма і трикутника, формувати уміння і навички перенесення раніше набутих знань до вивчення нового, накопичувати методи й прийоми розв’язування задач.

Розвиваюча мета: активізувати пізнавальну діяльність учнів, розвивати вміння міркувати, аналізувати, робити висновки.

Виховна мета: підвищення інтересу до геометрії, уважності, творчої ініціативи.

Хід уроку

І. Актуалізація опорних знань

1. Якими могли б бути сторони прямокутника, якщо його площа 8 см²?

2. Якими будуть сторони квадрата, площа якого 8 см²?

3. Як зміниться площа прямокутника:

А) якщо одну сторону зменшити в 2 рази, а іншу збільшити в 2 рази? (не зміниться)

Б) усі сторони збільшити в 2 рази? (збільшиться в 4 рази)

В) якщо дві протилежні сторони зменшити в 2 рази? (зменшиться в 2 рази)

Г) якщо дві протилежні сторони збільшити в 6 разів, а дві інші – зменшити в 3 рази? (збільшиться в 2 рази)

3. Яка властивість площі використана вами при складанні танграма при виконанні домашнього завдання (Площа многокутника дорівнює сумі площ окремих многокутників і дорівнює 100 см²).

ІІ. Мотивація навчальної діяльності. Оголошення теми і мети уроку.

Кому необхідно більше фарби: людині, якій потрібно пофарбувати пластинку прямокутної форми розміром 8 см і 16 см чи пластинку у формі паралелограма зі сторонами 16 см і висотою, проведеною до неї – 8 см? (Припущення учнів).

Працюємо з паперовою моделлю (моделі роздані до початку уроку в учнів на парті). Розрізаємо паралелограм по висоті і переносимо відрізаний трикутник зліва направо. Які висновки можна зробити?

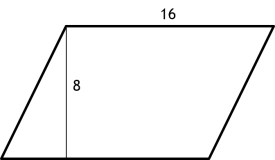
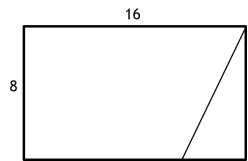
(З паралелограма можна отримати прямокутник і навпаки. Дані фігури рівновеликі.)

ІІІ. Сприйняття та усвідомлення формул площі паралелограма і трикутника.

Робота з GeoGebra. Базові задачі 8 клас https://www.geogebra.org/m/wJcn3cGd

Розповідь учнів, що працювали вдома з даними моделями.

Учень1. Користуючись тим, що з паралелограма легко можна отримати прямокутник і навпаки та тим, що дані фігури рівновеликі, допоможу всім вивести формулу площі паралелограма. В паралелограмі ABCD проведемо дві висоти BB₁ i CC₁, отримаємо (за катетом і гіпотенузою) △ABB₁ = △DCC₁;

Учень 2. Користуючись прямокутником, можна легко знайти площу трикутника і допоможе мені в цьому така модель:

1) Спочатку розглянемо прямокутний △ABC, добудуємо його до прямокутника ABCD. S_ABCD = AD * AC, △ABC = △DCB, S_△ABC = ½ AB * AC.

2) Розглянемо довільний △АВС і добудуємо його до паралелограма, △АВС = △DCB, S_△ABC = ½ S_ABDC.

Щоб знайти площу паралелограма, потрібно провести висоту ВН і тоді S_△ABC =

= ½ AС * ВН.

Так як в трикутнику можна провести три висоти, то його площу можна обчислювати за формулами:

S = ½ a*h_a = ½ b*h_b = ½ c*h_c,

Площа трикутника дорівнює половині добутку сторони та висоти, проведеної до неї.

Учень 3. Попрацюємо з паперовими моделями паралелограма,що знаходяться у вас на парті  і відріжемо бокові трикутники. Ви, напевно, помітили, що положення точки А на ваших моделях різне. Як ви вважаєте, чи рівні за площею трикутник, що залишився та сума двох відрізаних? Як це перевірити? (Накладанням). Накладіть їх на середній та зробіть висновок. (Площі рівні).

Скористаємося наступною моделлю: https://www.geogebra.org/m/wJcn3cGd#chapter/100971

За допомогою цієї моделі можна знайти ще й числові значення площі трикутника і площі паралелограма, якщо ввести відповідні дані.

ІV. Формування умінь і навичок застосування вивчених формул до розв’язування задач.

 (Завдання на слайдах або роздруковані на аркушах)

1) Встановити відповідність

1. Площа прямокутника зі сторонами 6 см і 8 см.

2. Площа паралелограма зі стороною 6 см і висотою, проведеною до неї, 3 см.

3. Площа прямокутного трикутника зі сторонами 6, 8, 10 см.

4. Площа трикутника зі стороною 8 см і висотою проведеною до неї, 3 см.

А. 12 см²

Б. 480 см²

В. 18 см²

Г. 24 см²

Д. 48 см²

1 – Д,     2 – В,     3 – Г,     4 – А.

2) Розв’язування задач за готовими малюнками

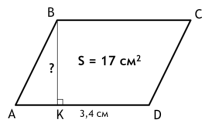Задача 1.

BK = 17 : 3,4 = 5 (cм)

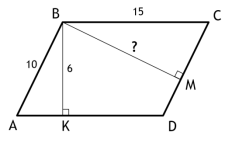Задача 2.

            S_ABCD = BK x BC = 6 x 15 = 90

         S_ABCD = BM x DC = 90

     BM = 90 : 10 = 9

Задача 3.

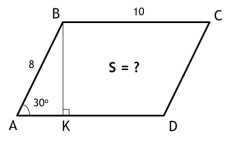
BK = 4

       S_ABCD = BC x BK = 4 x 10 = 40

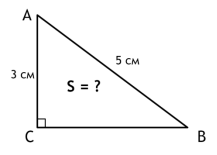Задача 4.

                       BC = 4

          S_ABC = 0,5 x AC x BC = 0,5 x 3 x 4 = 6(см²)

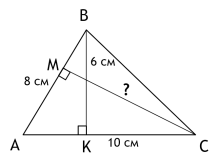Задача 5.

                                S_ABC = 0,5 x BK x AC = 0,5 x 6 x 10 = 30 (см²)

         S_ABC = 0,5 x MC x AB = 30 (см²)

MC = = 7,5 (см)

При розв’язуванні даної задачі мова про площу трикутника не йшла, але ми використали її для знаходження невідомої висоти. В геометрії такий прийом називають метод площ для знаходження невідомих елементів.

3) Цікаві факти про площу

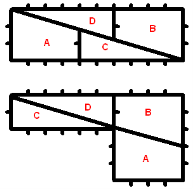
Чому жінки люблять переставляти меблі?

Напевно тому, що збільшується площа кімнати.

Площа фігури АВСD дорівнює 3∙10 = 30.

Переставимо все місцями.

Маємо: площа фігури СD – 2∙6 = 12 і фігури АВ - 4∙5 = 20.

Тобто загальна площа 32.

Звідки ці дві одиниці?

V. Підведення підсумків.

Домашнє завдання (за підручником Геометрія 8 клас. А. Г. Мерзляк): Опрацювати п. 21-22, №706, №729, №734. Підготувати цікаві факти про площі з використанням ресурсу http://map1965.narod.ru/matematik_7.html

.