Урок "Побудова діаграм. Принципи побудови графіків"

Побудова діаграм

Діаграма – це представлення даних таблиці в графічному вигляді, яке використовується для аналізу і порівняння.

При побудові діаграми двомірна таблиця перетворюється у двовимірну графічну картинку. 

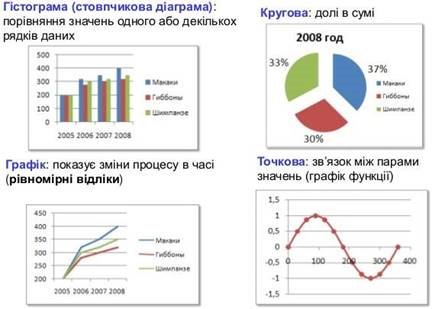Діаграми бувають різних типів:         кругові,      стовпчасті, лінійчасті, графіки, тощо. Для їх зображення або побудов використовуються також різні методи (алгоритми) побудов.

Розглянемо приклад побудови стовпчастої діаграми (гістограми).

На вертикальній осі (Y) розміщуються числові значення, а на горизонтальній осі (Х) – категорії. Побудуємо діаграму, за наступним зразком:

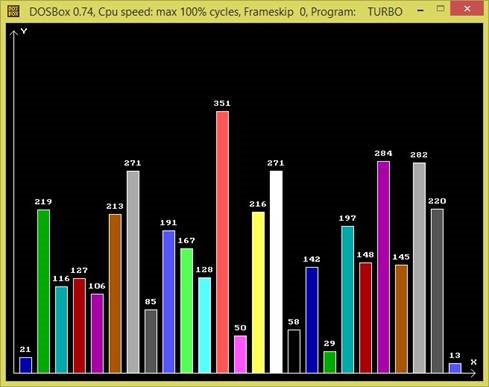
Висоти стовпців вибрані випадковим чином. 

На перший погляд написання даної прогррами здається складним і довгим процесом, але неасправді це не так. Для початку розіб’ємо нашу програму на складові частини:

I.                    Побудова осей

II.                 Побудова стовпців діаграми

Для кращої наочності, відступимо від країв екрану по 10px з кожного боку, і проведемо вертикальну та горизонтальну осі, разом зі стрілками. 

Для спрощення коду введемо деякі корективи. Для змінної X надамо значення максимальної координати по осі 0X, а змінній Y – максимальне значення координати по осі 0Y.

X:=GetMaxX;

Y:=GetMaxY;

I.                    Побудова осей

Для побудови використаємо процедуру Line.

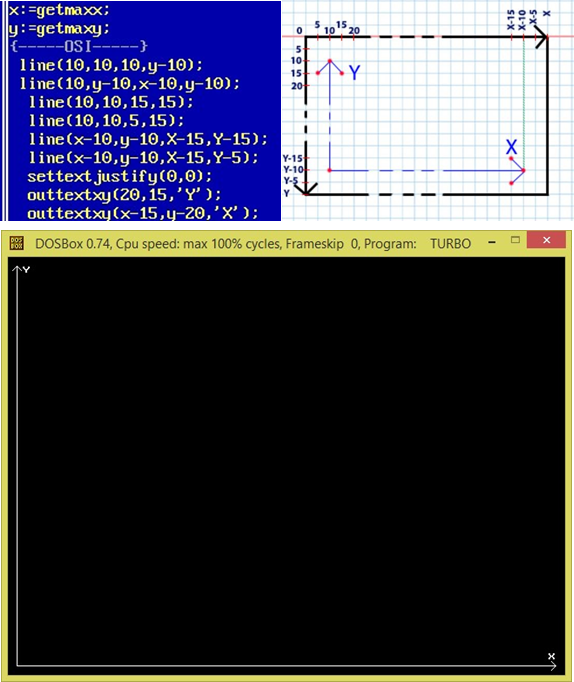
Для виведення тексту в графічному режимі використовують процедуру OutTextXY(X, Y : Integer; Text : String), де X,Y –точка виведення тексту, Text – значення, або змінна типу String – текст, який буде виводитись.

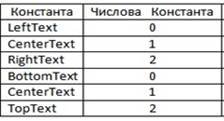Для вирівнювання, відносно точки координат тексту використовують процедуру SetTextJustify(Horiz, Vert : Word) – параметр Horiz вирівнює текст по горизонталі, параметр Vert – по вертикалі, та можуть набувати значень від 0 до 2. При заданні параметрів (1,1) точка з координатами буде по центру тексту, (0,0) – лівий нижній кут, (2,2) – правий верхній кут.  

II.                 Побудова стовпців діаграми

Для виконання даного етапу необхідно використати циклічний алгоритм, адже побудова великої кількості стовпців через задання координат вручну є досить трудомістким і не зручним методом. Також він не підійде для тих випадків, коли кількість стовпців наперед не задано. Тому для вирішення даного завдання необхідно вивести універсальні координати для кожного стовпця, які б залежали лише від його порядкового номера.

Для початку побудуємо та розберемо модель прикладу діаграми, що має 3 стовпці.

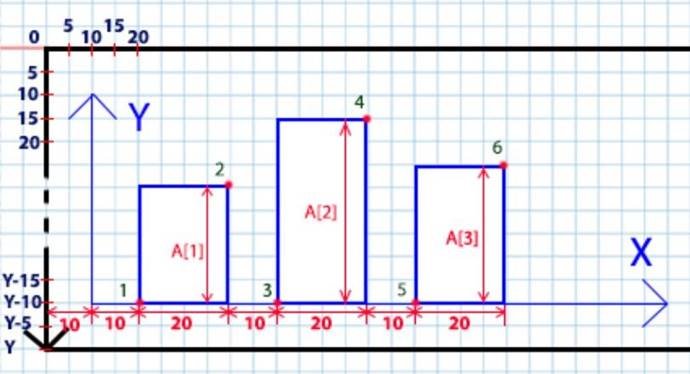
Відступи від країв екрану прийняли по 10px; Відступи між стовпцями також візьмемо за 10px; Ширину стовпців задамо як 20px.

Розрахуємо спочатку координати на осі 0Х. Для побудови будемо використовувати процедуру Bar, оскільки вона дозволяє побудувати зафарбований прямокутник.

Для першого стовпця:

1.      10+10;

2.      10+10+20;

Для другого стовпця:

3.      10+10+20+10;

4.      10+10+20+10+20;

Для третього стовпця:

5.      10+10+20+10+20+10;

6.      10+10+20+10+20+10+20;

Числові значення навмисне не додаємо, для подальшого спрощення, та виведення універсальних координат.

Отже, як бачимо, в попередніх виразах є певні елементи, які є спільними для різних стовпців. Друга координата кожного стовпця більша за першу на 20 (точки 2, 4, 6). При відношенні попарно координат між собою, то всі вони відрізняються на (10+20), наприклад, точки 1, 3, 5:

Для першого стовпця:

1. 10+10;

Для другого стовпця:

3. 10+10+20+10;

Для третього стовпця:

5. 10+10+20+10+20+10;

Спростимо дані вирази:

Для першого стовпця:

1. 10+10;

Для другого стовпця:

3. 10+(10+20)+10;

Для третього стовпця:

5. 10+(10+20)+(10+20)+10;

Тепер спостерігається деяка закономірність, майже в кожному стовпці зустрічаються і повторюються вирази (10+20). Спробує дещо скоротити  вирази, домноживши вирази в дужках на їх кількості.

Для першого стовпця:

1. 10+10+(10+20)*0;

Для другого стовпця:

3. 10+10+(10+20)*1;

Для третього стовпця:

5. 10+10+(10+20)*2;

Після простих перетворень маємо схожі вирази. Тепер прив’яжемо множники дужок до порядкових номерів стовпців.

Для першого стовпця:

1. 10+10+(10+20)*(1-1);

Для другого стовпця: 3. 10+10+(10+20)* (2-1);

Для третього стовпця:

5. 10+10+(10+20)* (3-1);

Оскільки побудова прямокутників буде здійснюватися за допомогою циклу, то для створення універсального виразу можна використати параметр циклу, котрий, якраз, і буде мати значення порядкового номера діаграми. Отже остаточний вигляд універсальної координати бля першої точки прямокутника буде наступним: 

x1=10+10+(10+20)* (i-1);

Як розглядалося вище, друга координата відрізняється від першої лише на 20, тоді: x2=10+10+(10+20)* (i-1)+20;

Тепер визначимо координати по осі 0Y. Тут буде значно простіше. Перша координата всіх діаграм починається з побудованої нами осі 0X, значить:

y1=GetMaxY – 10, або, для нашого випадку: y1=y-10;

Залишилося лише розібратись із висотами стовпців. Їх значення – це якраз та числова характеристика, яку саме і відображають за допомогою діаграми. Дані числові значення можна отримувати різними способами: за допомогою генератора випадкових чисел, введенням з клавіатури, через математичні розрахунки та зчитуванням з файлу. Для простоти програми використаємо генератор випадкових чисел. Отримані значення запишемо в одновимірний масив, що дозволить зручніше опрацьовувати дані за допомогою циклу. Отже, друга координата по осі 0Y матиме наступний вигляд:

y2=y-10-A[i];

Коли ми отримали остаточні координати, то можемо записати універсальний вираз, для побудови стовпців діаграми:

Bar(x1,y1,x2,y2)=>Bar(10+10+(10+20)* (i-1), y-10, 10+10+(10+20)* (i-1)+20, y-10-A[i]);

Тепер можна описати алгоритм, який буде здійснювати циклічні побудови.

for i:=1 to n do     begin      setfillstyle(1,i);

bar(10+10+(10+20)* (i-1), y-10, 10+10+(10+20)* (i-1)+20, y-10-A[i]); end;

n – кількість стовпців діаграми, 

setfillstyle(1,i); - параметр i в даній процедурі дозволяє розфарбовувати стовпці діаграми

різними кольорами.

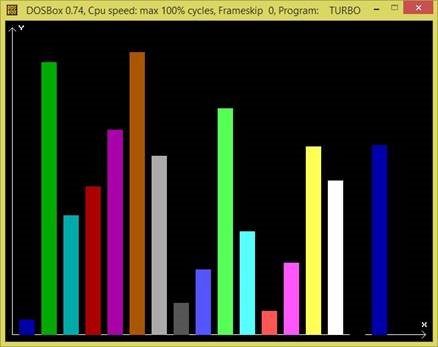
При побудові 17 стовпців діаграми бачимо, що 16-й не відображається. Насправді він має конкретне числове значення, а отже і висоту. Просто він не відображається через те, що має чорний (прозорий) колір, і на фоні не відображається. Обведемо всі елементи лініями білого кольору за допомогою процедури Rectangle:

for i:=1 to n do     begin      setfillstyle(1,i);

bar(10+10+(10+20)* (i-1), y-10, 10+10+(10+20)* (i-1)+20, y-10-A[i]); rectangle(10+10+(10+20)* (i-1), y-10, 10+10+(10+20)* (i-1)+20, y-10-A[i]); end;

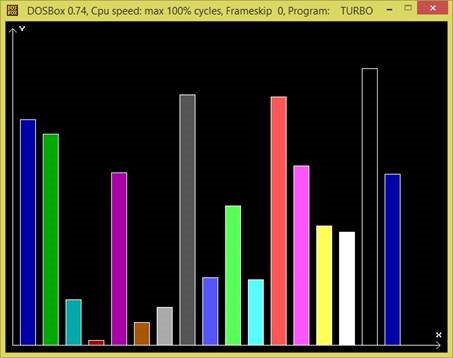
І тепер залишилося лише підписати числові значення. Для цього використаємо процедуру

OutTextXY. Також застосуємо процедуру STR(a,s) – переведення числового значення (a) у рядковий тип даних (s). Параметри Х та Y процедури OutTextXY задамо таким чином, щоб текст відображався

над стовпцями діаграми, та по середині їх ширини:

OutTextXY (10+10+(10+20)* (i-1)+10, y-10-A[i]10,s);

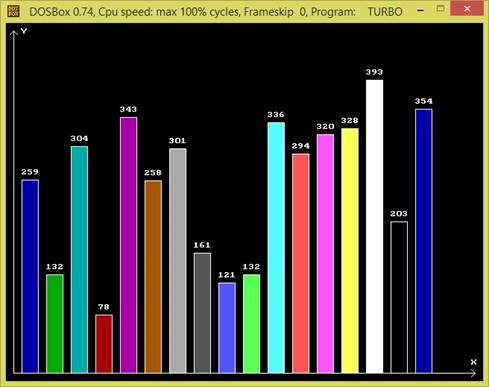
Остаточний варіант програми:

Uses graph,crt; var gd,gm:integer;     y,x:integer;     n,i:integer;     s:string;

a:array [1..20] of integer; begin gd:=detect; initgraph(gd,gm,'..\bgi');

  if graphresult<>0 then writeln('ERROR')    else      begin

x:=getmaxx; y:=getmaxy;  line(10,10,10,y-10);  line(10,y-10,x-10,y-10); line(10,10,15,15);   line(10,10,5,15);   line(x-10,y-10,X-15,Y-15); line(x-10,y-10,X-15,Y-5);   settextjustify(0,0);   outtextxy(20,15,'Y'); outtextxy(x-15,y-20,'X');

randomize;    for i:=1 to n do     a[i]:=random(400); settextjustify(1,1);    for i:=1 to n do     begin      setfillstyle(1,i);

bar(10+10+(10+20)* (i-1), y-10, 10+10+(10+20)* (i-1)+20, y-10-A[i]); rectangle(10+10+(10+20)* (i-1), y-10, 10+10+(10+20)* (i-1)+20, y-10-A[i]); str(a[i],s);

outtextxy(10+10+(10+20)* (i-1)+10, y-10-A[i]10,s);     end;   end; readln; closegraph; end.

В даній програмі є один недолік, це те, що при побудові малої кількості стовпців не використовується вільне місце, а при побудові більше ніж 20 – вони просто не поміщаються на екрані, тому для цього необхідно ввести певні коефіцієнти пропорційності, які і будуть містити числові значення, що відповідають за ширину стовпців, та відступи між ними. Для розрахунку коефіцієнтів для X-координати виконаємо наступні дії. Спочатку визначимо максимально допустиме місце для побудови: x-10-10-10 (відступи від країв екрану, та стрілки).

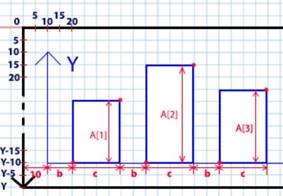Потім дану величину розділимо на кількість стовпців, щоб визначити кількість місця, яке буде відведене для побудови одного елемента (сегмента) діаграми    (стовпець, та         відступ           перед ним).   В попередньому прикладі в нас це було (10+20): 

w:=(x-30) div n. 

де n – кількість стовпців. Умовно візьмемо, що на відстань між стовпцями виділяється 1/3 сегмента, а для стовпця виділимо 2/3:

b:=w div 3; c:= b*2; Отже, вирази для побудови тепер матимуть наступний вигляд:

   n:=25;    w:=(x-30) div n;    b:=w div 3;    c:=b*2;    randomize;    for i:=1 to n do     a[i]:=random(400);    settextjustify(1,1);    for i:=1 to n do     begin setfillstyle(1,i);

bar(10+b+(c+b)*(i-1),y-10,10+b+(c+b)*(i-1)+c,y-10-a[i]); rectangle(10+b+(c+b)*(i-1),y-10,10+b+(c+b)*(i-1)+c,y-10-a[i]);      str(a[i],s); outtextxy(10+b+(c+b)*(i-1)+c div 2,y-10-a[i]-10,s); end;

Для розрахунку коефіцієнта розтягу по вертикалі (d), потрібно визначити максимально можливе значення, доступне для побудови (h), та максимальний елемент масиву висот (max). Для визначення максимального доступного значення для побудови на осі 0Y скористаємось попереднім виразом:  h=y-10-10-10. 

Для знаходження найбільшої висоти елементів використаємо алгоритм пошуку максимального елемента масиву: max:=a[1]; for i:=2 to n do

    if max<a[i] then max:=a[i];

Тепер можна визначити коефіцієнт розтягу по вертикалі:

h:=y-30; d:=h div max;

Після виконання всіх цих перетворень ми отримаємо наступні результати: (для 5 стовпців):

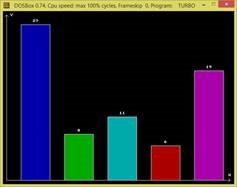
 Код програми Uses graph,crt; var gd,gm:integer;     y,x:integer; n,i,w,b,c,max,h,d:integer;     s:string;     a:array [1..20] of integer; begin gd:=detect; initgraph(gd,gm,'..\bgi');

  if graphresult<>0 then writeln('ERROR')

else      begin

x:=getmaxx; y:=getmaxy;  line(10,10,10,y-10);  line(10,y-10,x-10,y-10); line(10,10,15,15);   line(10,10,5,15);   line(x-10,y-10,X-15,Y-15); line(x-10,y-10,X-15,Y-5);   settextjustify(0,0);   outtextxy(20,15,'Y'); outtextxy(x-15,y-20,'X');    n:=25; w:=(x-30) div n;    b:=w div 3;    c:=b*2;    randomize;    for i:=1 to n do     a[i]:=random(400);    settextjustify(1,1); max:=a[1]; for i:=2 to n do     if max<a[i] then max:=a[i];    h:=y-30; d:=h div max;

for i:=1 to n do     begin      setfillstyle(1,i);

     bar(10+b+(c+b)*(i-1),y-10,10+b+(c+b)*(i-1)+c,y-10-a[i] *d);      rectangle(10+b+(c+b)*(i-1),y-10,10+b+(c+b)*(i-1)+c,y-10-a[i] *d); str(a[i],s);      outtextxy(10+b+(c+b)*(i-1)+c div 2,y-10-a[i]*d-10,s);     end;   end; readln; closegraph; end.