Урок (практична робота) Обчислення основних статистичних характеристик вибірки. Візуалізація даних. Інфографіка.

ПРАКТИЧНА РОБОТА

МЕТА: Навчити студентів використовувати можливості Excel для обчислення основних вибіркових характеристик,    сформувати уявлення про інфографіку, згадати правила побудови діаграм і графіків в Excel, навчити аналізувати дані, що відображає інфографіка. Виховувати творчу  активність.

Обладнання: ПК, робочий зошит, тестові завдання

В результаті виконання практичної роботи студент повинен

знати

• правила введення формул та функцій;
• поняття відносної і абсолютної адресації;
• призначення і види функцій для статистичних розрахунків;
•  Яким сполученням клавіш користуються для підтвердження опрацювання даних масиву?
• правила побудови діаграм в Excel;
• переваги використання інфографики.

вміти:

•      використовувати формули для розрахунків в таблиці;
•      користуватися статистичними функціями;
•      виконувати копіювання формул;

•      будувати діаграми і графіки;
•      Вводити формули для масиву.

Тривалість роботи 2 години

Питання для підготовки до практичної роботи

1. Для чого використовують статистичні дослідження?
2. Які основні характеристики вибірки?
3. Як в Excel можна вставити функцію? Як її скопіювати7
4. Як в Excel побудувати діаграму чи графік? Як його модифікувати?
5. Які типи діаграм ви знаєте?
6. Що таке інфографіка?
7. Які переваги використання Інфографіки.

Короткі теоретичні відомості

Для аналізу кількісних характеристик використовують статистичні дослідження. Кожне дослідження складається, по-перше, із отримання кількісних даних і, по-друге, — для проведення аналізу дані піддаються статистичному опрацюванню.

Дані для дослідження називають статистичними даними (вибіркою).

У статистичному аналізі опрацьовуються такі характеристики ви­бірки.

Обсяг вибірки — кількість елементів у вибірці.

Розмах вибірки — різниця між максимальним і мінімальним значеннями елементів вибірки.

Середнє арифметичне ряду чисел — це частка від ділення суми цих чисел на їх кількість (обсяг вибірки).

Мода ряду чисел — число, яке найчастіше зустрічається в ряді даних. Якщо дані у вибірці не повторюються, мода не обчислюється. Якщо в ряді даних є числа, які зустрічаються однакову кількість разів, мода буде мати кілька значень.

Медіана впорядкованого ряду чисел з непарним числом чле­нів — число, яке виявиться посередині. Медіана впорядкованого ряду чисел із парним числом членів — середнє арифметичне двох чисел, за­писаних посередині. Отже, половина значень вибірки менше за медіану, а половина більше.

Частота — число повторень значень вибірки в заданих інтер­валах.

Відносна частота — це відношення частоти до загальної кіль­кості даних у вибірці.

Стандартне відхилення (ще його називають середньоквадратичним відхиленням, СКВ) — показник розсіювання статистичних даних відносно середнього значення вибірки.

Дослідження, експерименти, статистичний аналіз завжди супроводжуються візуалізацією даних. Графіки й діаграми не тільки графічно відображають значення, а й мають змістове навантаження щодо теми дослідження. Відразу видно загальну картину результатів дослідження, ве­лику кількість даних на обмеженому проміжку. Крім того, акцентується увага на деяких елементах ряду даних, порівнюються фрагменти даних, демонструється тенденція зміни властивостей, що досліджуються, тощо.

Інфографіка (від латин. informatio — інформування, роз'яснення, і грец. урафікос — письмовий) — це візуальне відображення інформації, стати­стичних даних для простої і наочної демонстрації тенденцій, співвідно­шень, а також зацікавлення в предметі дослідження

Для змістового навантаження графіка чи діаграми важливо пра­вильно вибрати їх тип. Розглянемо різні типи діаграм на прикладах.

Гістограми використовують для наочного подання динаміки зміни да­них у часі або розподілу даних у вигля­ді прямокутних областей, розмір яких відповідає значенням, отриманим у ре­зультаті статистичного дослідження.

рис. 5.1.  Приклад гістограми

На нормованих плоских гістограмах із накопиченням відображається відсоткова частка кожного значення в загальному підсумку для різних категорій.

Кожного року Український центр оцінювання якості освіти опри­люднює результати статистичного аналізу ЗНО. На рис. 5.2. подано лінійчасту діаграму складання ЗНО з української мови учнями Кропивницького (джере­ло: https://zno2017.monitoring.in.ua/). Результати відображені по навчальних закладах, тому кожна смуга відповідає за результати типу НЗ, а кольором позначено інтервали балів.

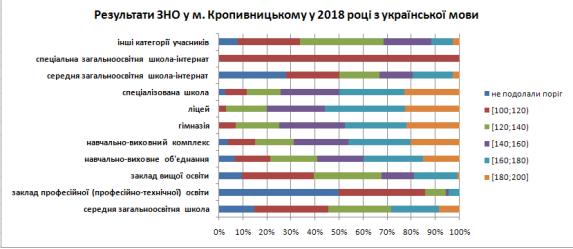
рис.5.2. Приклад гістограми з накопиченням

Кругові діаграми ви­користовують для наочного зображення співвідношення між частинами вибірки ко­ристуються круговими діа­грамами. На рис. 5.3. відображена доля кожної спеціальності у загальній кількості студентів набору 2018 року.

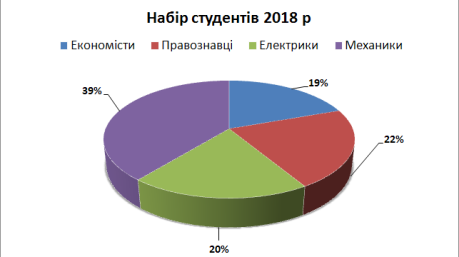
рис.5.3. Кругова діаграма

Полігоном частот називають ламану з вер­шинами у точках (z_і, n_i), i = 1, 2, ..., k. Тут z_i — значення і-ї варіанти, а п_i — відповідна цій варі­анті частота.

Для побудови полігона частот на осі абсцис відкладають варіанти z„ а на осі ординат — відповідні частоти. Точки (z_і, n_i) сполучають відрізками прямих і отримують полігон частот.

По суті, полігон частот — це графіч­не зображення ін­тервального ряду.

У цьому прикладі ми покажемо, як використовувати MS Excel для побудови полігону частот. Вважаємо, що таблиця частот вже побудована. Виділимо в ній два стовпці: значення ряду (вони будуть відкладатися по осі Ox) та відносні частоти (будуть відкладатися по Oy). Тепер Майстер діаграм. Він попросить нас відповісти на 4 питання:

1. Визначити тип графіка (точкова діаграма, на якій значення з'єднані відрізками);
2. Вказати вихідні дані (вони вже обрані: X - значення, Y - частоти);
3. Задати додаткові параметри оформлення (можна не ставити);
4. Вказати місце для розміщення діаграми (за замовчуванням - на цьому ж аркуші).

Полігон частот готовий:

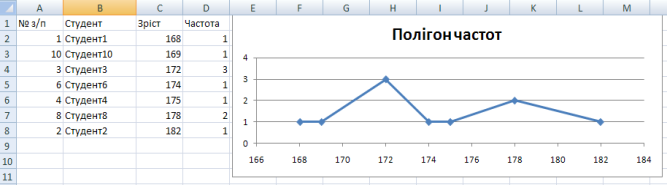
рис.5.4. Приклад побудови полігону частот

Завдання для практичного виконання

Увага! Під час роботи з комп’ютером дотримуйтеся вимог безпеки життєдіяльності та санітарно-гігієнічних норм.

Завдання на 4-6  бали

1.    Скопіюйте файл ДО ЛПЗ 5(11) до власної папки та відкрийте його. Перейменуйте Лист1 на: Завдання 1.
2.    Введіть дані  в таблицю, за допомогою автозаповнення та відформатуйте її за зразком.

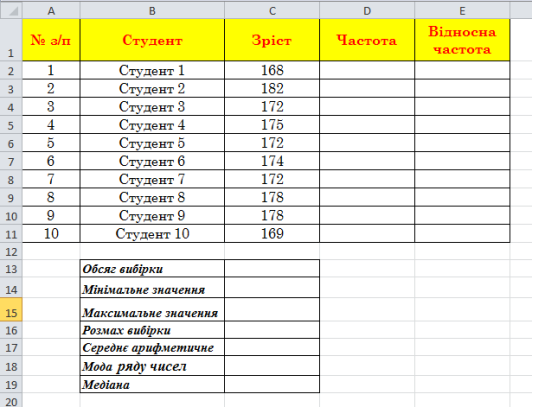
1. Для цього  введіть в клітинку А2 - 1, в А3 - 2. Об’єднайте  діапазон А1:А2 і потягніть за маркер авто заповнення   поки не побачите 10.
2. У клітинку B2 введіть «Студент1». Натисніть Enter і  потягніть за маркер авто заповнення до клітинки В11. Що відбулося?
3. Дані про зріст введіть з додаткової цифрової клавіатури.

3. Дані в стовпці Зріст впорядкуйте за зростанням. Для цього станьте у колонці Зріст і натисніть кнопку
4. Використовуючи статистичні функції MS Excel, розрахуйте основні характеристики ви­бірки. Результати і функції, які ви використовували запишіть у звіт. Вставка – Функции -  зі списку Категория вибрати Статистические

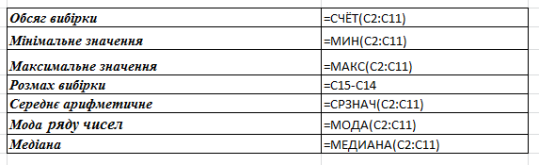
1. У комірці D2 вставити функцію =ЧАСТОТА(C2:C11;C2:C11)
2. Виділяємо діапазон D2:D11. Натискаємо F2, а потім комбінацію клавіш CTRL+SHIFT+ Enter. У цьому випадку формула діє на масив даних
3. У комірці E2 розрахувати відносну частоту за формулою =D2/$C$13. (Зробіть адресу С13 абсолютною, для цього натисніть F4). Скопіюйте формулу на весь діапазон.

5. Порівняйте отримані результати зі зразком.

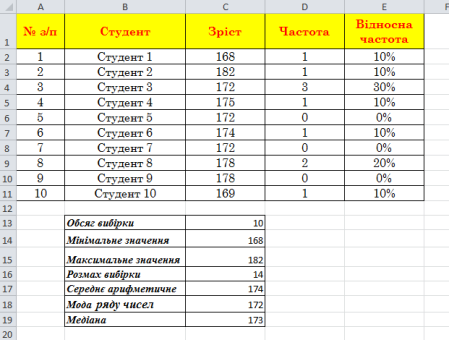
6. Перейдіть на лист Завдання 2 і за даними таблиці побудуйте кругову діаграму по зразку з теоретичних відомостей (рис.5.3. Кругова діаграма).
7. Продемонструйте результат викладачу.

Завдання на 7-8 балів

8. Перейдіть на лист Завдання 3 і на підставі даних про температуру у вересні розрахуйте основні характеристики вибірки. Порівняйте отримані результати із зразком.
9. На листі Завдання 3 за даними таблиці побудуйте гістограму по зразку з теоретичних відомостей (рис. 5.1.  Приклад гістограми)
10. Перейдіть на лист Завдання 4 і за даними таблиці побудуйте Нормовану гістограму з накопиченням по зразку з теоретичних відомостей (рис.5.2. Приклад гістограми з накопиченням)
11. Запишіть у звіт які навчальні заклади дали найбільший відсоток учнів, що не подолали поріг, а які дали найбільший відсоток максимальних балів.

Завдання на 9-10 балів

12. Перейдіть на лист Завдання 5 і на підставі даних про Середню заробітну плату в Україні у 2018 році розрахуйте основні характеристики вибірки.
13. На підставі даних про середню ЗП побудуйте гістограму.
14. Звірте результати

15. Виконайте наступні дії з гістограмою:
    1.                 Скопіюйте побудовану діаграму.
    2.                 Перенесіть її на окремий лист.
    3.                 Змініть її тип на «Графік з маркерами»
    4.                 Додайте лінію тренду
    5.                 Виведіть рівняння лінії тренду на графіку
    6.                 Запишіть у зошит висновок

Завдання на 11-12 балів

16. Перейдіть на лист Задання 5. Додайте колонку Середня ЗП після місяця Липень і розрахуйте середню ЗП по кожному регіону.
17. Скопіюйте назви регіонів і середню ЗП на новий аркуш. Назвіть його Задання 6. Додайте колонку Ранг і визначте місце кожного регіону по показнику середня ЗП.
18. Відсортуйте за рангом по зростанню. Запишіть у звіт яке місце займає Кіровоградська область.
19. Визначте медіану по середній зарплаті. Запишіть у звіт її значення. Скільки значень у вибірці менше медіани? Скільки більше? Зробіть висновок.
20. Побудуйте полігон частот по рис.5.4. Приклад побудови полігону частот (див. теоретичні відомості)
21. Закінчіть роботу.

Виконайте дома.

• Створіть інфографіку, яка б відображала ваш розклад дня. Скільки часу ви спите, навчаєтесь, відпочиваєте, тощо. Намагайтеся використовувати різні технології, щоб результат був якнайкращим.
• Розмісіть роботу на Google-диску та відправте копію викладачу на адресу mstrizeus@gmail.com

Приклад інфографіки