Урок "Побудова графіка функції за допомогою першої та другої похідної"

Тема уроку: побудова графіка функції за допомогою першої та другої          похідної.

Мета:

навчальна:      - узагальнити знання учнів про функціональну залежність;

                           - удосконалювати вміння будувати графік функціональної

       залежності на основі дослідження функції за допомогою

       похідної;

розвиваюча:    - розвивати кмітливість, творчі здібності, логічне мислення;

                           - формувати математичну мову;

                           - тренувати пам’ять;

                           - встановлювати зв’язок між вивченим;

виховна:          - виховувати зацікавленість у пізнанні нового;

              - виховувати уважність, зібраність, спостережливість,

     працьовитість, самостійність.

Хід уроку

I Організаційний етап

II Перевірка домашнього завдання  (підручник А.Г. Мерзляк і інші)

   № 1.6 (1,3)

№ 14.8(1)

Знайти проміжки опуклості та точки перегину функцій

y=x³-2x²+x-2 

Y´=3x²-4x+1

Y₺=6x-4

6x-4<0       y₺>0   опукла вниз

x> , функція опукла вниз  на [;+∞)

6x-4<0;  y₺<0    опукла вгору

X< ,  функція опукла вниз на [;+∞)

X= -точка перегину.

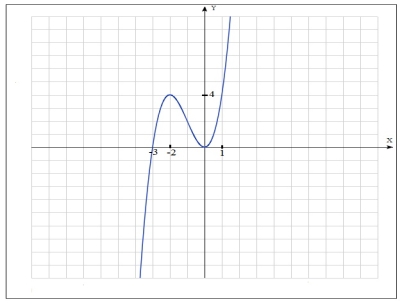
№ 15.2(1)  Побудувати графік функції         f(x)=x³+3x²  

III  Мотивація навчальної діяльності.

Сучасні фахівці повинні добре володіти математичними знаннями. Використання диференціального числення є дуже важливим в різних сферах нашого життя. Функції зустрічаються часто на практиці. Вони описують рух, фізичні явища. Зустрічаються в геометрії, хімії, механіці, економіці.

IV  Вивчення нового матеріалу

№ 15.7

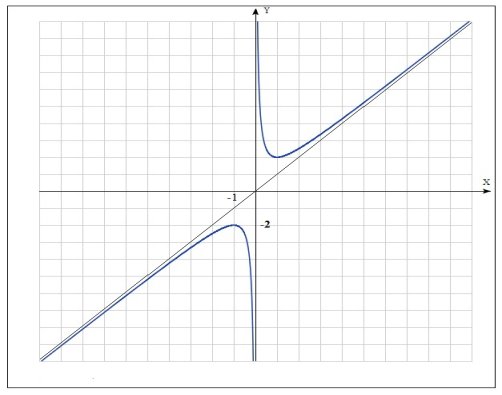
Побудуйте графік функції        f(x)=x + .

1. Область визначення   -  множина дійсних чисел.
2. Дослідити функцію на парність.  f(x)=-f(x) -  функція непарна. Графік симетричний відносно початку відліку О(0;0).

Періодичність функції -   неперіодична.

3. Знаходимо точки перетину графіка з координатними осями:

З віссю ОХ:    у=0

Х²+1≠0,      нулів функція немає.

З віссю ОУ:   х≠0,    точок перетину немає.

4. Знайти проміжки зростання і спадання.     Знаходимо похідну, прирівнюємо до 0. Маємо :

Х₁=1;  Х₂=-1;

Х=-1  точка максимуму; у_max=-2,

Х=1   точка мінімуму; у_min=2,

5. Асимптоти:

а) вертикальні в точках розриву функції, х=0 – вертикальна.

б) похилі шукаємо у вигляді :  у=кх+b, де

к= .     К=1.

b =  0,  у=х.

6. Y´=(1- 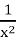) = 1- х^-2

Y₺=2х^-3 = ,  

якщо х>0,   Y₺>0  опукла вниз (0;+∞). Якщо х<0, Y₺<0  опукла вгору.

max              min   

V Підсумок уроку

Засвоїли навички і уміння досліджувати функції та будувати їх графіки.

VI Домашнє завдання . Повторити параграф 15,  № 15.8(1), 15.10.