Урок-подорож з алгебри і початків аналізу для учнів 10 класу за темою "Найпростіші тригонометричні рівняння та рівняння, які зводяться до них"

КЗ «НСЗШ І – ІІІ ступенів №9»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Машина часу у світі Тригонометрії

 

 

Урок з алгебри і початків аналізу у 10 класі за темою:
Найпростіші тригонометричні рівняння

та рівняння, які зводяться до них

 

 

 

 

 

 

 

 

 

 

Розробив і провів:

учитель математики

                       Л.О. Дяченко

 

 

 

 

 

м. Нікополь

Машина часу у світі Тригонометрії

 

У кожного теперішнього є своє майбутнє,  яке осяює його і яке зникає разом з ним, стаючи минулим-майбутнім.

                     Жан-Поль Сартр

 

Урок  узагальнення та перевірки знань, вмінь і  навичок за темою:

Найпростіші тригонометричні рівняння

та рівняння, які зводяться до них

Мета: повторити алгоритм розв'язування найпростіших   тригонометричних рівнянь, перевірити рівень їх засвоєння; закріпити вміння і навички учнів розв'язувати рівняння, які зводяться до найпростіших тригонометричних рівнянь; формувати навички самостійної роботи; розвивати навички самоаналізу, самоконтролю та взаємоконтролю, вміння аналізувати ситуацію, увагу, мислення; виховувати культуру спілкування і почуття взаємодопомоги.

Формування компетентностей:

Соціальна компетентність: самостійне розв'язування завдань різними способами, самооцінка і взаємооцінка.

Комунікативна компетентність: повідомлення презентацій, взаємоперевірка

Інформаційна компетентність: використання додаткової інформації, створення презентацій, розв'язування завдань ЗНО.

Полікультурна компетентність: зв'язок з іншими предметами

Продуктивна творча діяльність: використання творчих завдань

  Тип уроку: комбінований (з застосуванням міні-проекту та інтерактивних технологій).

Тригонометричні функції широко застосовуються в математиці, фізиці й техніці. Безліч процесів описуються функціями, які задаються формулами  у = А sin (ωх+φ) або у = А cos (ωх+φ), де А , ω, φ – задані числа, А0, ω0. Такі процеси називають гармонічними коливаннями. Гармонічні коливання найчастіше є функцією часу. Тому ми сьогодні подорожуватимемо умовною машиною часу. Час має три напрями: минуле, теперішнє і майбутнє. Виходячи з цього, урок складатиметься з трьох частин.

• «Минуле» матиме за мету освітити історію тригонометрії, за допомогою презентацій учнів  пригадати сфери практичного застосування тригонометричних функцій та шляхом проведення гри «математичне лото» перевірити елементарні практичні навички учнів з розв`язування найпростіших тригонометричних рівнянь з подальшою самоперевіркою.
•  «Теперішнє» відтворюватиме картину стану засвоєння практичних вмінь та навичок з розв'язування рівнянь, які зводяться до найпростіших тригонометричних рівнянь, та буде спрямоване на їх узагальнення. Так як теперішнє – це коловорот подій сьогодення, то пропонується процес узагальнення та корекції практичних вмінь та навичок здійснити у вигляді інтерактивної вправи «Карусель». Учні

І-их варіантів не змінюють своїх місць знаходження, а учні ІІ-их варіантів починають рух, змінюючи своє місцеперебування за годинниковою стрілкою. Учням І-их варіантів видані блоки завдань, які вони послідовно розв`язуватимуть з учнями, які до них сідатимуть. Таких завдань буде чотири, на виконання кожного з них відведено 3 хвилини, а п'яте завдання всі учні виконуватимуть самостійно. На дошці відтворюватиметься процес послідовного запису отриманих відповідей учнями ІІ-их варіантів (перший записує відповідь до першого завдання і т.д.) і оцінка їх вчителем (пропонується невербальна оцінка поруч із записом відповіді        ,        ,        ). Учні перевіряють свої записи, звіряючи їх із записами на дошці, та виставляють по 1 балу за кожну правильну відповідь у персональну картку самооцінки.

• «Майбутнє» зараз недосяжне, але завжди здається, що воно буде кращим за теперішнє. Тому вчитель пропонуватиме учням завдання з підготовки до ЗНО, завдання творчого характеру, у яких потрібно за відомим розв'язком скласти умову рівняння, та індивідуальні домашні завдання на картках.

Для здійснення роботи на уроці кожному з учнів будуть видані персональні картки з записаними на них напрямами часу і завданнями, а також картки самооцінки.

 

Картка самооцінки
1	2	3	4	5	6
1	2	3	4	5	6
Набрані бали

Інформація, яка буде зазначена на картках з завданнями,  у більш розгорнутому вигляді наведена далі.

Перший етап –  «Минуле».

Теперішньому, щоб стати майбутнім, необхідне минуле.

Йосип Бродський

Промова вчителя. Ваше минуле пов'язане з виконанням домашнього завдання та підготовкою презентацій. Перевіримо правильність виконання домашнього завдання, яке є одним з прикладів практичного використання знань з тригонометрії. Вдома необхідно було розв'язати наступну задачу:

 Міська електрична мережа живиться змінним електричним струмом. Його сила І змінюється за законом гармонічних коливань:

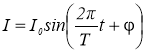, де I₀ – максимальне значення сили струму; Т – період коливань; φ – початкова фаза. У які моменти часу сила струму досягає максимального значення?

 

 

Промова вчителя. Прослухаємо варіанти отриманих відповідей і звіримось з записом на дошці. Тригонометричні рівняння як і тригонометричні функції мають широке практичне застосування у різноманітних сферах життя людини. За допомогою презентацій, підготовлених учнями, пригадаємо ці сфери.

Учні демонструють міні-проект: презентації за темами «Тригонометричні функції у фізиці», «Тригонометричні функції в біології», «Тригонометричні функції в медицині», «Тригонометричні функції в астрономії». За підготовлену і продемонстровану презентацію учні виставляють 1 бал в картку самооцінки.

Після прослуховування презентацій, учням пропонується гра «Математичне лото». Мета: виконати завдання з перевірки вмінь та навичок з розв'язування найпростіших тригонометричних рівнянь та здійснити самоперевірку результатів роботи.

Математичне лото

Умова: у відведених квадратах на картці учні зазначають номер умови, що відповідає записаній відповіді.

Завдання для І-го варіанту:

 

 

1)  cos x = 0;      

2)  sin 4x = 1;

3)  ;

4)  ;     

5)  ;

6)  .

Завдання для ІІ-го варіанту:

 

1)  cos x = 1;        

2)  ;       

3)  ;      

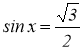4)  ;

5)  ;

6)  .

 

Відповіді до гри «Математичне лото»

Варіант І               Варіант ІІ

3	5	1		5	3	1
2	6	4		4	6	2

 

«Теперішнє»

 

Якщо бажаєш змін у майбутньому – зміни своє теперішнє.

Махатма Ганді

Для участі у етапі «Теперішнє» учням пропонується участь у інтерактивній вправі «Карусель». Мета: узагальнити і перевірити вміння та навички розв'язувати рівняння, які зводяться до найпростіших тригонометричних, порівняти свої розв'язки з розв'язками сусідів по грі та остаточно звіритись з записами на дошці, зазначивши отримані бали (по 1 за кожну правильну відповідь) у картці самооцінки.

Схема здійснення руху учнів під час інтерактивної вправи «Карусель»

 

 

 

 

 

 

 

 

 

 

 

 

 

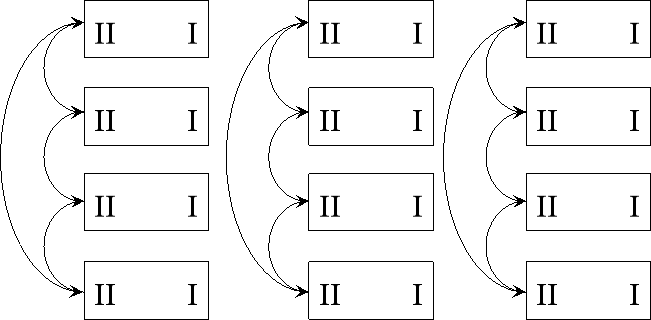
Завдання для інтерактивної вправи «Карусель»:

 

1)  2 sin²x = 7sinx + 9;

2)  cos7x + 3sin7x = 0;

3)  ;

4)  ;

5)  cosx  + cos5x = cos2x (самостійно);

«Майбутнє»

 

Поки живемо майбутнім, воно в нас є.

Аркадій Давидович

 

Майбутнє, як відомо, кидає свою тінь задовго до того, як увійти.

Анна Ахматова

 Промова вчителя. У майбутньому кожному з Вас доведеться відшукати свій життєвий шлях і майбутню професію. Багато професій вимагають знань з математики, тому пропоную для тих, хто набрав найбільшу кількість балів, витягнути білети  з запропонованими додатковими особливими завданнями. Ваша мета: розв'язати завдання на дошці та прокоментувати його. У разі успішного виконання, кожен з учасників поставить в картку самооцінки додатковий бал.

Завдання з підготовки до ЗНО:

1. Роз'яжіть рівняння  2π sinx = arcctg.
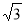2. Скільки коренів має рівняння  sin²x + cos²x = π + х на проміжку х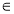[0; π].
3. Скільки коренів має рівняння  cosx = x³.
4. Скільки коренів має рівняння  sinx = x².

Завдання творчого характеру.

За зазначеними коренями рівнянь складіть умови рівнянь:

1.  ,  ;
2. ,  ;
3. ,  ;
4. , .

  

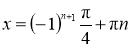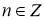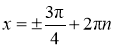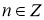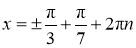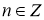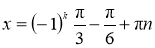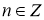Для домашнього розв`язання учням будуть запропоновані  чотири види карток:

Теперішньому, щоб стати майбутнім, необхідне минуле. Йосиф Бродський   Розв'яжіть рівняння: ; ; ; .	Справжня щедрість по відношенню до майбутнього полягає у тому, щоб усе віддавати теперішньому. Альбер Камю Розв'яжіть рівняння: ; ; ; .
Мислення – це мій рух і рух моїх знань у часі. Шарль Вінтер   Розв'яжіть рівняння: ; ; ; .	Якщо бажаєш змін у майбутньому – зміни своє теперішнє Махатма Ганді   Розв'яжіть рівняння: ; ; ; .

Підведення підсумку уроку. Повідомлення результатів.

 

Найвища  майстерність –
радіти досягнутому.

                       А.П.Садчиков

  Промова вчителя. Тригонометрія знайшла своє почесне місце у нашому житті, і сфери, в яких вона відіграватиме важливу роль, будуть поширюватись.

   Після завершення уроку учні зазначають психоемоційний стан у відведених місцях на картці самооцінки і здають картки і роботи  вчителеві.