Урок "Показникові рівняння та нерівності."
Тема уроку: Показникові рівняння та нерівності.
- Усні завдання на застосування властивостей показникової функції.
У завданнях 1, 2, 3, 4 назвати номери правильних варіантів.
- Які з наведених функцій є показниковими?
1) у = 3х; 2) у = х3; 3) у = 1х;
4) у = (-4)х; 5) у = ![]() ; 6) у = х0,6;
; 6) у = х0,6;
7) у = (х – 5)8; 8) у = (1 - ![]() )х; 9) у = 9-х;
)х; 9) у = 9-х;
10) у = х-х; 11) у = πх; 12) у = ![]() .
.
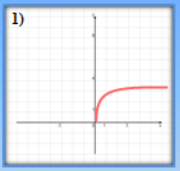
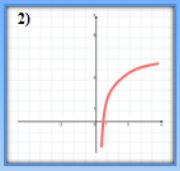
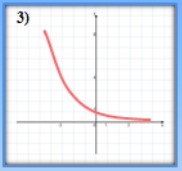
- Які з наведених графіків є графіками показникової функції?
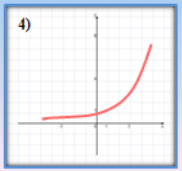
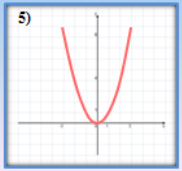
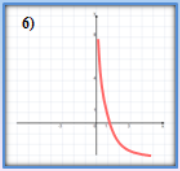
- Серед наведених функцій виберіть ті, що зростають.
- у = 2х ; 2) у = 100,5х ; 3) у =0,65х+2 ; 4) у = 0,151,5х;
5) у ![]() ; 6) у =
; 6) у = ![]() .
.
- Серед наведених функцій виберіть ті, що спадають.
1) у = 40,3х ; 2) у = 0,3х ; 3) у = 6,92х-1 ; 4) у = 0,112х ;
5) у = ![]() ; 6
; 6![]() у
у ![]() 7) у =
7) у = ![]()
- Порівняйте числа m і n, якщо:
-
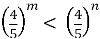 ; то m n 2)
; то m n 2) 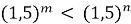 ; то m n
; то m n
![]() 4)
4) ![]() ; то m n
; то m n
- Подайте у вигляді степеня з основою 2 число:
8=![]() ;
; ![]() ; 0,25=
; 0,25=![]() ;
; ![]() =
=![]()
- Подайте у вигляді степеня з основою 3 число:
81=![]() ;
; ![]()
![]() ;
; ![]()
![]() ; 1
; 1![]() .
.
- Усне розв’язування показникових рівнянь і нерівностей.
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
2х = 16 |
3х-1 = 9 |
3х = |
12х = 1 |
27х = 3 |
|
2 |
2х > 8 |
|
2х > -2 |
2х < -2 |
|
- Класифікація показникових рівнянь та нерівностей.
Назвіть способи розв’язування рівнянь. Записати в таблицю порядкові номери відповідних рівнянь і нерівностей.
|
Зведення до спільної основи |
Винесення спільного множника за дужки |
Введення нової змінної (заміна) |
Однорідне рівняння (нерівність) |
|
Р |
Р |
Р |
Р |
|
Н |
Н |
Н |
Н |
|
1. 3х
2.
3.
|
6. 5∙4x - 7∙10x +2∙ 25x = 0. |
4. 4·
5. 2х+2-2х+1+2х-1-2х-2
6. 32х+1-28·3х+9
|
|
7. (0,6)х-3
8. 5-2х-4-5-2х-5-2·5-2х-6
9. |
- Письмове розв’язування показникових рівнянь і нерівностей.
№1. Розв’яжіть рівняння ![]() ;
;

№2. Розв’яжіть нерівність ![]() .
.

- Робота в парі.

- Підсумок уроку.Оцініть свою роботу на уроці не загальноприйнятими балами, а за своєю шкалою, враховуючи свої очікування від уроку.
ДД – дуже добре
|
|
Д – добре
ЗК – знає, але не каже
КЗ – каже, але не знає
ГНК – гірше нема куди
1
Тема уроку: Показникові рівняння та нерівності.
Мета уроку:
- удосконалити знання та вміння учнів розв’язувати показникові рівняння та нерівності;
- систематизувати методи розв’язування показникових рівнянь та нерівностей;
- розвивати логічне мислення, самостійність, уміння зосередитися,
-розвивати вміння аргументувати свої дії, формулювати висновок, чітко будувати свою відповідь;
- виховувати почуття відповідальності, віру у свої можливості й здібності;
- виховувати уміння сконцентруватися, слухати інших, співпереживати;
- формувати вміння співпрацювати в ході спільної навчальної діяльності.
Тип уроку: урок узагальнення та систематизації знань.
Форма організації уроку: колективна, групова, індивідуальна, фронтальна.
Хід уроку
І. Організаційний етап.
ІІ. Повідомлення теми і мети уроку.
Вступне слово вчителя. Які асоціації викликає у мене слово «урок»?
У – успіх…
Р – радість…
О – обдарованість…
К – компетентність…
Сподіваюся, сьогодні на нас чекає і успіх, і радість. Ви зможете продемонструвати власну обдарованість і компетентність. Перед вами стоїть завдання проявити свої знання і вміння застосовувати властивості показникової функції при розв’язуванні рівнянь та нерівностей.
ІІІ. Мотивація навчальної діяльності.
За допомогою математики можна розв’язувати задачі, що виникають у життєвих ситуаціях і стосуються реальних об’єктів або процесів. За допомогою показникової функції можна описати:
-
Радіоактивний розпад речовини
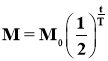 ,
,
де M – маса речовини через час t, M0 – початкова маса речовини, T – період напіврозпаду.
-
Розмноження бактерій
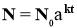 ,
,
де No – початкова кількість бактерій, N – кількість бактерій в момент часу t, а і k - деякі сталі.
-
Нарощування капіталу
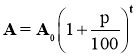 ,
,
де A – шукана величина, A0 – початкова сума, p – річний відсоток, t – розрахунковий термін.
- Швидкість руйнування адреналіну в крові, швидкість зміни кількості ліків у організмі
![]() ,
,
де A(t) – кількість ліків у організмі через час t, A0 – швидкість надходження ліків до організму, k – коефіцієнт пропорційності.
Отже, вміння застосовувати властивості показникової функції при розв’язуванні показникових рівнянь та нерівностей застосовуються в різних галузях науки.
ІІІ. Узагальнення й систематизація знань та вмінь.
- Бліц-опитування (фронтальна робота)
Запитання до учнів:
- Яка функція називається показниковою?
- Яка область визначення показникової функції?
- Яка область значень показникової функції?
- При якій умові показникова функція є зростаючою? Дайте визначення зростаючої функції.
- При якій умові показникова функція є спадною? Дайте визначення спадної функції.
- Яке рівняння називають показниковим?
- Яка нерівність називають показниковою?
- Що, крім властивостей показникової функції, ми використовуємо при розв’язуванні показникових рівнянь і нерівностей?
- Усні завдання на застосування властивостей показникової функції.
У завданнях 1, 2, 3, 4 учні повинні назвати номери правильних варіантів.
- Які з наведених функцій є показниковими?
1) у = 3х; 2) у = х3; 3) у = 1х;
4) у = (-4)х; 5) у = ![]() ; 6) у = х0,6;
; 6) у = х0,6;
7) у = (х – 5)8; 8) у = (1 - ![]() )х; 9) у = 9-х;
)х; 9) у = 9-х;
10) у = х-х; 11) у = πх; 12) у = ![]() .
.
(відповідь: 1, 5, 9, 11, 12)
- Які з наведених графіків є графіками показникової функції?
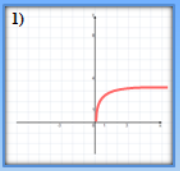
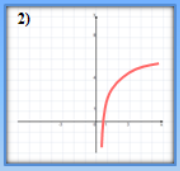
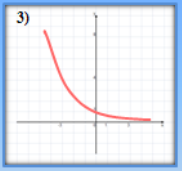
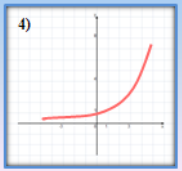
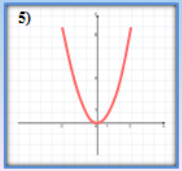
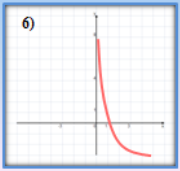
(відповідь: 3,4)
- Серед наведених функцій виберіть ті, що зростають.
- у = 2х ; 2) у = 100,5х ; 3) у =0,65х+2 ; 4) у = 0,151,5х;
5) у ![]() ; 6) у =
; 6) у = ![]() .
.
(відповідь: 1, 2, 6, 7)
- Серед наведених функцій виберіть ті, що спадають.
1) у = 40,3х ; 2) у = 0,3х ; 3) у = 6,92х-1 ; 4) у = 0,112х ;
5) у = ![]() ; 6
; 6![]() у
у ![]() 7) у =
7) у = ![]()
(відповідь: 2, 4, 5, 7)
- Учням пропонується порівняти числа m і n та обгрунтувати свою відповідь.
Порівняйте числа m і n, якщо:
-
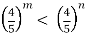 ; (а = 4/5, а < 1, то m > n)
; (а = 4/5, а < 1, то m > n)
2) ![]() ; (а = 1,5, а > 1, то m < n )
; (а = 1,5, а > 1, то m < n )
![]() (а = 0,3, а < 1, то m < n)
(а = 0,3, а < 1, то m < n)
4) ![]() ; (а = 8/3, а > 1, то m > n)
; (а = 8/3, а > 1, то m > n)
- Подайте у вигляді степеня з основою 2 число:
8; ![]() ; 0,25;
; 0,25; ![]() .
.
(Відповіді: 8 = 23; ![]() ;
; ![]() 0,25 = 2-2;
0,25 = 2-2; ![]() )
)
- Подайте у вигляді степеня з основою 3 число:
81; ![]() ;
; ![]() ; 1.
; 1.
(Відповіді: 81 = 34; ![]() = 3-3;
= 3-3; ![]() =
= ![]() ; 1 = 30 )
; 1 = 30 )
- Усне розв’язування показникових рівнянь і нерівностей.
Учням пропонується таблиця з найпростішими показниковими рівняннями та нерівностями.
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
2х = 16 |
3х-1 = 9 |
3х = |
12х = 1 |
27х = 3 |
|
2 |
2х > 8 |
|
2х > -2 |
2х < -2 |
|
- Класифікація показникових рівнянь та нерівностей.
Назвіть способи розв’язування рівнянь:
Учні записують в таблицю порядкові номери відповідних рівнянь і нерівностей.
|
Зведення до спільної основи |
Винесення спільного множника за дужки |
Введення нової змінної (заміна) |
Однорідне рівняння (нерівність) |
|
Р |
Р |
Р |
Р |
|
Н |
Н |
Н |
Н |
|
1. 3х
2.
3.
|
6. 5∙4x - 7∙10x +2∙ 25x = 0. |
4. 4·
5. 2х+2-2х+1+2х-1-2х-2
6. 32х+1-28·3х+9
|
|
7. (0,6)х-3
8. 5-2х-4-5-2х-5-2·5-2х-6
9.
|
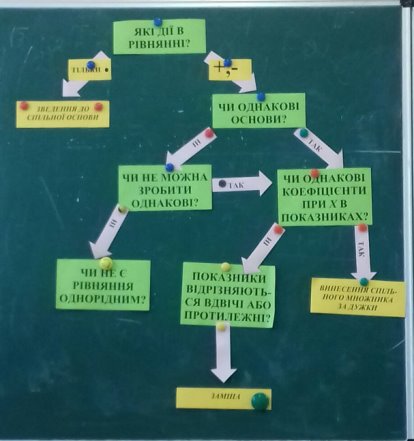
Підсумком роботи над цим завданням є складена спільними зусиллями схема, яка допомагає розв’язувати показникові рівняння та нерівності.
-
Письмове розв’язування показникових рівнянь і нерівностей.
- Колективне розв’язування.
Два учні біля дошки пропонують метод та обґрунтовують свій вибір.
№1. Розв’яжіть рівняння ![]() ;
;
Розв’язання.
![]() ;
;
![]()
![]() ;
;
![]() ;;
;; ![]() ;
; ![]()
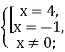
Відповідь: -1;4.
№2. Розв’яжіть нерівність ![]() .
.
Розв’язання.
Зведемо всі степені до двох основ 4 і 9:
![]() .
.
Маємо однорідну нерівність (у всіх членів однаковий сумарний степінь – 2х). Для її розв’язування поділимо обидві частини на ![]() .
.
![]() .
.
Заміна ![]() дає нерівність
дає нерівність ![]() ; звідки
; звідки ![]()
Обернена заміна: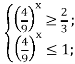
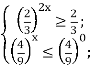
![]()
![]()
Відповідь: [0;0,5].
Робота в парах.
Кожна пара учнів залежно від запасу власних умінь і навичок розв’язує на свій розсуд одне рівняння та одну нерівність з завдання «Класифікація показникових рівнянь та нерівностей». Але методи їх розв’язування повинні бути різними!
(Учні вибирають завдання, розв’язують їх в зошитах. Вчитель контролює процес, може надати додаткове завдання. Відводиться час 10 хв).
|
1. 3х
|
x=1 x=3 |
2.
|
2х (22-1)= 96; 2х = 32;
|
3.
|
x=-0,5 |
4. 4·
|
|
|
5. 2х+2-2х+1+2х-1-2х-2
|
|
6. 32х+1-28·3х+9
|
( x=2
( x=-2
|
7. (0,6)х-3
|
|
8. 5-2х-4-5-2х-5-2·5-2х-6
|
x=2
|
9.
|
IX. Підсумки.
Підсумком бесіди з узагальнення та систематизації набутих учнями знань із теми «Методи розв’язування показникових рівнянь та нерівностей» є складена спільними зусиллями схема.
Метод: «Своя система оцінювання». Учні оцінюють свою роботу на уроці не загальноприйнятими балами, а за своєю шкалою, враховуючи свої очікування від уроку.
ДД – дуже добре
Д – добре
ЗК – знає, але не каже
КЗ – каже, але не знає
ГНК – гірше нема куди
На закінчення хочу нагадати вам, що завтра – знову урок алгебри, та роздати невеличкі презенти – індивідуальні завдання домашньої роботи. Замість ![]() кожен учень отримує натуральне число більше 1.
кожен учень отримує натуральне число більше 1.
Розв’яжіть рівняння та нерівності:
-
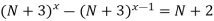 ;
;
-
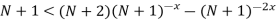 ;
;
-
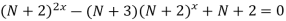 ;
;
-
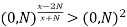 ;
;
-
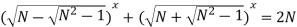 .
.
Дякую вам за урок! Хочу наприкінці уроку навести вислів великого Леонардо да Вінчі: «Якщо запастися терпінням і виявити старання, то посіяні насіння знання неодмінно дадуть добрі сходи». Що ми і перевіримо завтра на контрольній роботі.
(Відповіді до домашнього завдання: 1) 1; 2) (-1;0); 3) 1;0;
4) ![]() ; 5)
; 5) ![]() .
.
1


про публікацію авторської розробки
Додати розробку