Урок повторення теми "Вектори на площині"
Тема. Вектори
Мета:
- систематизувати знання з теми «Вектори»;
- формувати вміння застосовувати вивчені означення і властивості до розв’язування задач;
- розвивати кмітливість, увагу,самоконтроль у навчанні
Інструкція до заняття:
- повторити теоретичний матеріал;
- розв’язати тестові завдання;
- розв’язати задачі

Теоретична скарбничка
Означення
Вектором називається напрямлений відрізок
![]()
![]()
![]()
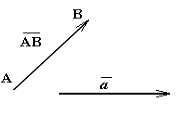
АВ = а; ![]() = АВ – модуль вектора АВ - це довжина відрізка АВ.
= АВ – модуль вектора АВ - це довжина відрізка АВ.
Рівні вектори
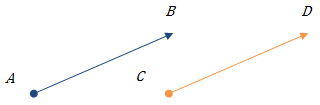
![]() =
= ![]()
![]() =
= ![]() , вектори
, вектори ![]() і
і ![]() однаково напрямлені
однаково напрямлені
Координати вектора
А1(х1; у1), А2(х2; у2)
![]()
![]()
А1 А2
![]() (а1; а2), де а 1= х2 – х1, а2 = у2 – у1,
(а1; а2), де а 1= х2 – х1, а2 = у2 – у1,
![]()
Презентація «Вектори на площині»
Задача 1
Доведіть, що чотирикутник з вершинами в точках А(-4;1), В(1;3), С(3;1), D(-2;-1) є паралелограм.
Розв´язання.
Знайдемо координати векторів ![]() і
і ![]() :
: ![]() (5; 2),
(5; 2), ![]() (5; 2). Так як координати векторів рівні, то
(5; 2). Так як координати векторів рівні, то ![]() =
= ![]() , отже, відрізки АВ і DС рівні і паралельні. Тоді чотирикутник АВСD- паралелограм , що і треба було довести.
, отже, відрізки АВ і DС рівні і паралельні. Тоді чотирикутник АВСD- паралелограм , що і треба було довести.
Дії над векторами
Сума векторів
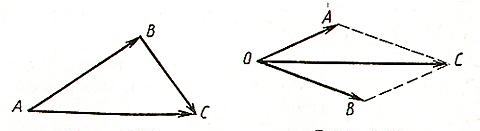
Правило трикутника Правило паралелограма
![]() +
+ ![]() =
= ![]()
![]() +
+ ![]() =
= ![]()
Різниця векторів
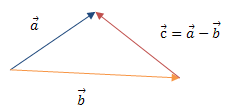
![]() (а1; а2) -
(а1; а2) - ![]() (b1; b2) =
(b1; b2) = ![]() (а1 - b1; а2; - b2)
(а1 - b1; а2; - b2)
Множення вектора на число
![]() (
(![]() ) = (
) = (![]() )
)
![]()
![]() А
А ![]() В
В ![]() С
С
![]() =
= ![]()
![]()
![]() =
= ![]()
При ![]()
![]()
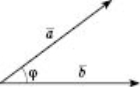 Скалярним добутком двох векторів називають добуток їх модулів і косинуса кута між ними
Скалярним добутком двох векторів називають добуток їх модулів і косинуса кута між ними
В координатах:
![]() (а1; а2),
(а1; а2), ![]() (b1; b2)
(b1; b2)
![]() = а1 b1 +а2b2
= а1 b1 +а2b2
![]()
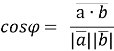
![]()
Відомості про практичне застосування
Задача
Дано точки А (3; - 4), В (- 2; 7), С (- 4; 16), D (1; 5). Довести, що ![]() =
= ![]() . Знаходимо координати
. Знаходимо координати ![]() (- 2 + 4; 7 - 16) = (
(- 2 + 4; 7 - 16) = (![]() ), і
), і ![]() (2; - 9).
(2; - 9).
Оскільки відповідні координати векторів рівні, то рівні й самі вектори.
Прикладна задача
Літак пролетів 200 км на південний захід, а тоді 300 км на захід. Зробіть відповідний рисунок за допомогою векторів. На якій відстані від початкової точки він опинився
Завдання. Складіть схожі задачі.
Перевір свої знання
Тест № 1
-
Знайти координати вектора
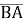 , якщо А (- 7; 5), В (4; -3)
, якщо А (- 7; 5), В (4; -3)
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Знайти абсолютну величину вектора
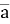 (-8; -2)
(-8; -2)
|
А |
Б |
В |
Г |
|
|
|
|
|
- Вектори додають за правилом:
|
А |
Б |
В |
Г |
|
трапеції |
паралелограма |
круга |
трикутника |
-
Знайти координати вектора
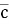 = 2
= 2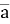 + 3
+ 3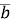 ,
, 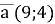 ,
, 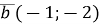
|
А |
Б |
В |
Г |
|
|
|
|
|
- Установіть відповідність між векторами (1-4) і співвідношення між ними (А-Д)
|
1 |
|
А |
вектори перпендикулярні |
|
2 |
|
Б |
вектори мають рівні довжини |
|
3 |
|
В |
вектори колінеарні |
|
4 |
|
Г |
вектори рівні |
|
|
|
Д |
сума векторів дорівнює вектору (8; -12) |
Розв´яжи сам
Задача 1
Відрізок АD- медіана трикутника АВC. Знайдіть модуль вектора ![]() , якщо А(-2; -1), В(3; 1), С(1;5).
, якщо А(-2; -1), В(3; 1), С(1;5).
Відповідь.4![]()
Задача 2
Точка М лежить на стороні ВС паралелограма АВСD, причому ВМ: МС= 3:1. Виразіть вектори ![]() і
і ![]() через вектори
через вектори ![]() =
= ![]() і
і ![]() =
= ![]()
Відповідь. ![]() +
+ ![]() ;
; ![]() -
- ![]() .
.
Задача 3
Знайдіть косинуси кутів трикутника ABC, якщо А(-1; 2), В(3;7).С(2;-1). Установіть вид трикутника АВС
Відповіді до завдань тестової роботи
|
№ завдання |
Відповідь |
|
1 |
Г |
|
2 |
А,В |
|
3 |
Б,Г |
|
4 |
Б |
|
5 |
1 – Д ; 2 – А 3 – Б; 4 – В |


про публікацію авторської розробки
Додати розробку
