УРОК-ПРАКТИКУМ Тема. ПАРАЛЕЛОГРАМ ТА ЙОГО ВЛАСТИВОСТІ.
УРОК-ПРАКТИКУМ
Так називають уроки розв’язування задач із однієї чи кількох пов’язаних тем. Основний час на практикумах відводиться на кероване самостійне розв’язування задач. Керівництво роботою може здійснюватись як учителем, так і за допомогою дидактичних матеріалів.
Готуючись до уроків-практикумів учителю треба зробити значну підготовчу роботу. Слід підготовити задачі середнього, достатнього та високого (творчого) рівнів складності, продумати форми їх представлення учням. Підібраний учителем дидактичний матеріал може містити: зразки розв’язування задач; вказівки; задачі з частиною розв’язування; розв’язування з пропусками; плани розв’язування; підказки-малюнки; допоміжні запитання; теоретичні довідки; ідеї та методи розв’язування; задачі з вибіркою відповіді тощо.
Методика проведення уроків-практикумів може бути такою. Учням із достатнім та високим рівнем навчальних досягнень пропонуємо відповідні задачі для самостійного розв’язування . У цей час під керівництвом учителя учні з низьким та середнім рівнем навчальних досягнень аналізують запропоновані задачі, записують розв’язування окремих із них. Далі ці учні переходять до самостійного розв’язування аналогічних задач, а учні разом з учителем аналізують розв’язування задач достатнього рівня, а потім розв’язують творчі завдання.
Біля дошки можуть працювати учні, розв’язуючи задачі різних рівнів складності мовчки. Розв’язування цих задач слід проаналізувати із класом у кінці року. Учні, які правильно розв’язували більшість задач, бажано поставити оцінки.
Тема. ПАРАЛЕЛОГРАМ ТА ЙОГО ВЛАСТИВОСТІ.
Мета. Систематизувати і узагальнити знання учнів по темі «Паралелограм та його властивості». Розвивати практичні уміння і навички при розв’язуванні задач. Виховувати культуру математичного мовлення, самостійність у навчальній праці.
Обладнання. Таблиці із задачами.
Хід уроку.
І. Перевірка домашнього завдання.
Гра «Вибери правильне твердження».
(Учні сигналізують, що твердження правильне сигнальними картками).
1. Чотирикутник, у якого 2 сторони паралельні, паралелограм (неправильне).
2. Чотирикутник, у якого 2 сторони рівні, паралелограм (неправильне).
3. Чотирикутник, у якого протилежні сторони паралельні , паралелограм (правильне).
4. Периметр паралелограма 30 см, а сума 2 сусідніх сторін 16 см(неправильне). А якою має бути сума 2 сусідніх сторін?
5. Чотирикутник, у якого діагоналі точкою перетину діляться пополам, паралелограм (правильне).
ІІ. Розв’язування задач.
- Усні задачі.
1. Чи може один із кутів паралелограма дорівнювати 40°, а другий 50°?
2. Відомо, що в паралелограмі один кут в 2 рази більший від другого. Чи є ці кути протилежними? Чому дорівнює сума цих кутів?
3. Сума двох кутів паралелограма 100°. Чи є ці кути прилеглими до однієї сторони паралелограма? Знайти кути паралелограма.
4. Сторони паралелограма дорівнюють 3 см і 5 см. Знайти його периметр.
5. Периметр паралелограма дорівнює 20 см. знайти його сторони, якщо:
а) одна з них на 2 см більша від другої;
б) вони відносяться як 3 : 7.
2. Задачі за готовим малюнком.
1. Які з чотирикутників, зображені на рисунку є паралелограмами?

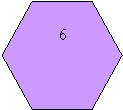
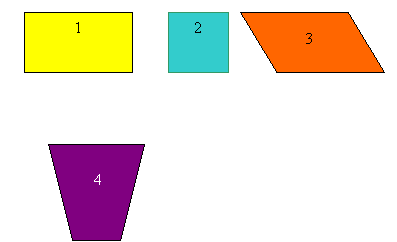
- Знайти кути паралелограма.
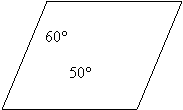
 B C
B C
![]() С
С
![]()
![]()
А D
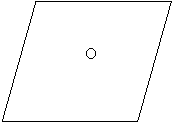

 B B C
B B C ![]() BOC =90°
BOC =90° ![]() OAD:
OAD: ![]() ODC=1:2
ODC=1:2
A D
- Довести, що АВСД – паралелограм.
![]() B C AO=OC
B C AO=OC
![]()
A D
3. Задачі практичного змісту.
1. Проведіть дві паралельні прямі. Відкладіть на одній із них відрізок АД, а на другій прямій – відрізок ВС, що дорівнює АД, так, щоб відрізки АВ і СД не перетиналися. Побудуйте відрізки АВ і СД.
а) Поясніть, чому чотирикутник АВСД є паралелограмом.
б) Позначте точку М так, щоб чотирикутник АВМС був паралелограмом. Чи лежать точки М, С, і Д на доній прямій?
2. Накресліть трикутник АВС і проведіть його медіану ВО. На промені ВО побудуйте відрізок ОД, що дорівнює ВО. Сполучіть точку Д з точками А і С.
а) Поясніть, чому чотирикутник АВСД є паралелограмом.
б) Позначте точку М так, щоб чотирикутник АВДМ був паралелограмом. Чи лежать точки М, С і Д на одній прямій?
4. Творчі завдання.
1. У паралелограма АВСД ВС=12 см, СД=7 см. Бісектриси кутів В і С, перетинаючи сторону АД, ділять її на три частини. Знайдіть кожну з них.
ІІІ. Підсумок уроку.
Оголошуються бали, які учні набрали в процесі розв’язування задач.
ІV. Домашнє завдання.
Знайти цікаві факти про паралелограм.


про публікацію авторської розробки
Додати розробку
